Изучение нового материала по теме: "Определенный интеграл и его свойства" 11 класс
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
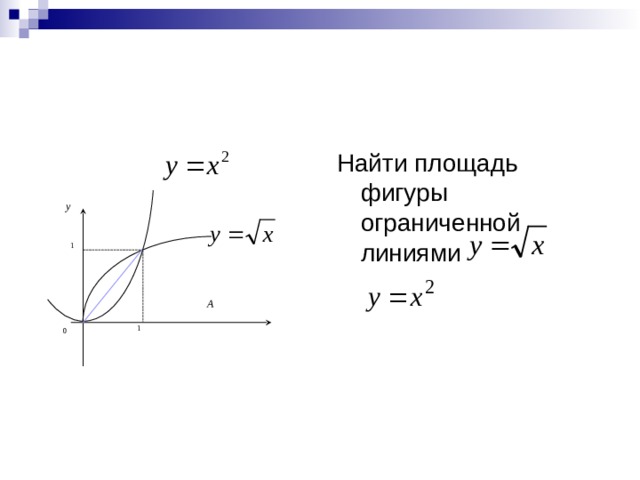
Определенный интеграл и его свойства
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Определенный интеграл и его свойства»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1800 руб.
3000 руб.
1910 руб.
3190 руб.
1540 руб.
2560 руб.
1430 руб.
2380 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства



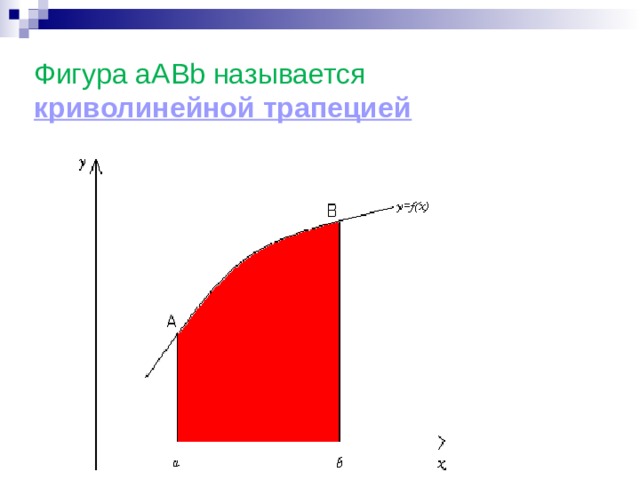
![Определенный интеграл Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей. Проведем через полученные точки прямые, параллельные оси OY. Заданная криволинейная трапеция разобьется на n частей. Площадь всей трапеции приближенно равна сумме площадей столбиков. по определению , его называют определенным интегралом от функции y=f(x) по отрезку [a;b] и обозначают так:](https://fsd.kopilkaurokov.ru/up/html/2019/11/20/k_5dd54ef11b9bb/img_user_file_5dd54ef2cb340_4.jpg)
![Теорема : Если функция непрерывна на отрезке [a, b] , а функция является первообразной для на этом отрезке, то справедлива формула: (3) формула Ньютона-Лейбница](https://fsd.kopilkaurokov.ru/up/html/2019/11/20/k_5dd54ef11b9bb/img_user_file_5dd54ef2cb340_5.jpg)




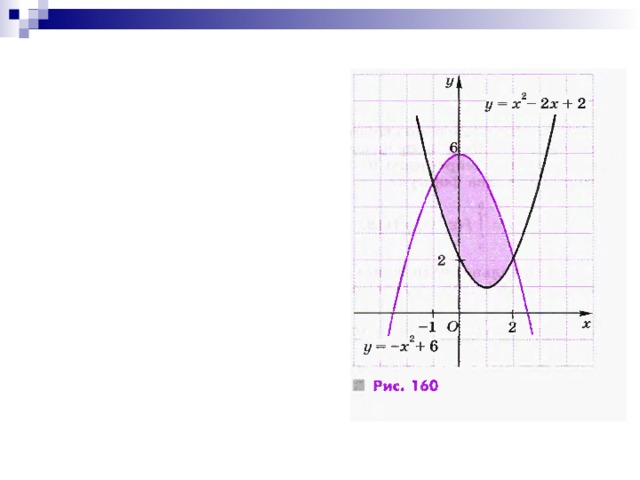
![Площадь фигуры, Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого x из [a;b], где a и b – абсциссы точек пересечения графиков функций:](https://fsd.kopilkaurokov.ru/up/html/2019/11/20/k_5dd54ef11b9bb/img_user_file_5dd54ef2cb340_15.jpg)