Государственное областное бюджетное
профессиональное образовательное учреждение
«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Методическая разработка
урока математики
«Определенный интеграл, его вычисление и свойства».
Выполнил: преподаватель математики
Заварзина В.Г.
Липецк 2016
Тема: «Определенный интеграл, его вычисление и свойства».
Цели урока:
Образовательные: 1) Систематизировать практические и теоретические знания, выработать умение находить неопределенный и определенный интегралы.
2) Развивать культуру устного вычисления определенных интегралов.
3) Содействовать развитию у студентов умений осуществлять самоконтроль, самооценку.
Развивающие: Развивать мышление и речь студентов, развивать навыки самостоятельного мышления, интеллектуальные навыки (анализ, синтез, сравнение, сопоставление), внимание, память.
Воспитательная: Содействовать воспитанию интереса к математике, активности, мобильности, аккуратности и внимательности.
Задачи урока:
1.Развитие познавательного интереса к предмету.
2.Воспитание самостоятельности, настойчивости при достижении конечного результата.
3.Формирование культуры учебной деятельности и информационной культуры.
Тип урока: комбинированный.
Методы обучения: фронтальный, индивидуальный, наглядно-практический.
Формы организации взаимодействия на уроке: учебная, групповая работа, индивидуальная работа.
Оборудование и наглядные средства обучения: мультимедийный проектор, интерактивная доска, презентация, демонстрационный и раздаточный материал.
Методическая цель: активизировать мыслительную деятельность студентов.
Ход урока.
1.Организационный момент.
Подготовка студентов к уроку (проверка отсутствующих на уроке, наличие тетрадей)
2. Актуализация опорных знаний.
Преподаватель.
Давайте вспомним историю возникновения интегралов.
Прошу послушать историческую справку об интеграле.
Историческая справка.
Сообщение студента.
Понятие интеграла и интегральное исчисление возникли из потребности вычислять площади (квадратуру) любых фигур и объёмы (кубатуру) произвольных тел.
Предыстория интегрального исчисления восходит к древности. Ученый, создавший интеграл. Евдокс Книдский (живший около 408-355 гг. до н.э.) – древнегреческий учёный. Он дал полное доказательство теоремы об объёме пирамиды; теоремы о том, что площади двух кругов относятся как квадраты их радиусов. При доказательстве он применил так называемый метод «исчерпывания», который нашёл своё использование (с некоторыми изменениями) в трудах его последователей.
Через две тысячи лет метод «исчерпывания» был преобразован в метод интегрирования, с помощью которого удалось объединить самые разные задачи – вычисление площади, объёма, массы, работы, давления, электрического заряда, светового потока и многие, многие другие.
Что представляет собой «метод исчерпывания» рассмотрим на простом примере.
Предположим, что надо вычислить объём лимона, имеющего неправильную форму, и поэтому применить какую-либо известную формулу объёма нельзя. С помощью взвешивания найти объём также трудно, так как плотность лимона в разных частях его разная.
Поступим следующим образом. Разрежем лимон на тонкие дольки. Каждую дольку приближённо можно считать цилиндром, радиус основания, которого можно измерить. Объём такого цилиндра вычислить легко по готовой формуле. Сложив объёмы маленьких цилиндров, мы получим приближенное значение объёма всего лимона. Приближение будет тем точнее, чем на более тонкие части мы сможем разрезать лимон.
Вслед за Евдоксом метод «исчерпывания» и его варианты для вычисления объёмов и площадей применял древний учёный Архимед. Успешно развивая идеи своих предшественников, он определил длину окружности, площадь круга, объём и поверхность шара. Он показал, что определение объёмов шара, эллипсоида, гиперболоида и параболоида вращения сводится к определению объёма цилиндра. Выражаясь современным языком, Архимед определил интегралы.
Что же такое интеграл? Слово «интеграл» произошло от латинского integer — целый, то есть целая, вся — площадь. Термин был предложен в 1696 г. Иоганном Бернулли.
Современное обозначение неопределенного интеграла было введено Лейбницем в 1675 году. Он адаптировал интегральный символ , образованный из буквы S — то есть от сокращения слова латинского summa (сумма). Преподаватель.Давайте повторим первообразные некоторых элементарных функций.

Преподаватель.
А теперь вспомним правила нахождения первообразных и формулу Ньютона-Лейбница.

Преподаватель.
Сейчас 4 студента выполнят тест на время. 30 секунд на обдумывание.
Ответы писать на листах теста.
1.Если для любого х из множества Х выполняется равенство F´(x) = f(x), то функцию F(x) называют … для функции f(x) на данном множестве.
А) производной; В) первообразной; С) обратной; D) непрерывной.
2.Совокупность всех первообразных функций F(x) + С для данной функции f(x) называется … функции f(x)
А) область определения; В) производной; С) область значения; D) неопределенным интегралом.
3.С помощью формулы Ньютона – Лейбница находят…
А) определенный интеграл; В) производную; С) обратную функцию;
D) неопределенный интеграл.
4. Найдите множество первообразных для функции f(x) = 2
А) 0; В) 2х + С; С) 2х; D) 2.
5. Криволинейной трапецией называется фигура, ограниченная сверху графиком функции у = f(x), снизу осью … , с боков прямыми … .
А) непрерывной функции; Ох; х = а, х = b; В) непрерывной, неотрицательной; у = а, у = b; Ох. С) непрерывной, неотрицательной; х = а, х = b; Оу.
Ответы:
| № вопроса | 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
|
|
|
| Вариант ответа | В | Д | А | В | А |
|
|
|
|
|
|
|
|
|
В это время студенты устно выполняют следующие задания.
Устная работа: (задания записаны на доске; цена ответа 1 балл)
1) Исправить ошибки в записи �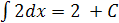 �;
�;
Ответ: ( 2x + C)
�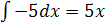 �.
�.
Ответ: (– 5x + C)
2) Найти интеграл:�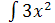 �dx;
�dx;
Ответ: (�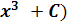 �
�
�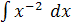 � ;
� ;
Ответ: ( �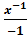 � + C = - �
� + C = - �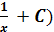 �
�
�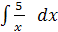 � .
� .
Ответ: ( 5 ln │x│)
3) Вычислить: �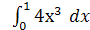 � ;
� ;
Ответ: (1)
�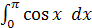 �
�
Ответ: ( sinπ - sin0 = 0 ).
3.Закрепление знаний.
Преподаватель.
Давайте решим следующие задания:
(Студенты выполняют задания.)
Задание 1.
Найдите неопределенные интегралы:
�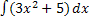 �; 2) �
�; 2) �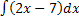 �; 3) �
�; 3) �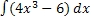 �; 4) �
�; 4) �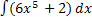 �
�
Ответы: 1) �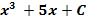 �; 2) �
�; 2) �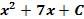 �; 3) �
�; 3) �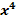 � - 6x + C; 4)�
� - 6x + C; 4)�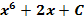 �
�
Задание 2.
Решаете на этих же листах.
1) �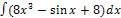 �; 2)�
�; 2)�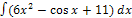 �; 3)�
�; 3)�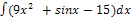 �;
�;
4) �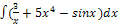 �.
�.
Ответы:
1) �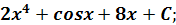 �
�
2)�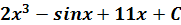 �;
�;
3)�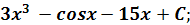 �
�
4)�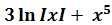 � + cos x+ C.
� + cos x+ C.
4. Самостоятельная работа.
Преподаватель.
А теперь сделайте задания самостоятельно.
Студенты выполняют задания по вариантам.
I Вариант.
Найдите определенные интегралы:
1)�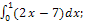 � 2) �
� 2) �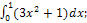 � 3)�
� 3)�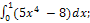 � 4)�
� 4)�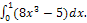 �
�
Ответы: 1)�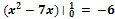 �; 2)�
�; 2)�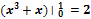 �; 3)�
�; 3)�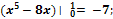 � 4)�
� 4)�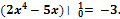 �
�
II Вариант.
Найдите определенные интегралы:
1)�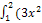 � + 5)dx; 2)�
� + 5)dx; 2)�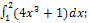 � 3)�
� 3)�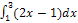 �; 4)�
�; 4)�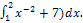 �
�
Ответы: 1)�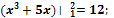 � 2)�
� 2)�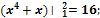 � 3)�
� 3)�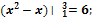 � 4)�
� 4)�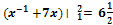 �
�
5.Домашнее задание.
Преподаватель.
Вычислите интегралы:
1)�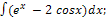 � 2) �
� 2) �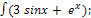 � 3) �
� 3) �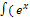 � + sinx)dx; 4) �
� + sinx)dx; 4) �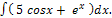 �
�
Ответы: 1) �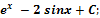 � 2) – 3 cosx + �
� 2) – 3 cosx + �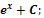 � 3) �
� 3) � � 4) 5sinx + �
� 4) 5sinx + � �
�
6.Подведение итогов.
Какие вычисления мы производили сегодня на уроке?
Рефлексия деятельности студентов на уроке.
-Что понравилось на уроке?
-Какой материал был наиболее интересен?
-Оцените свою работу на уроке: плохо работал, хорошо, отлично. Поднимите руки, кто работал плохо? Почему? И т.д.
- Как вы думаете, пригодятся ли вам знания данной темы в вашей будущей профессии?
Выставление оценок .
Список литературы:
1. Дидактические материалы по алгебре и началам анализа для 11 класса /Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. – М.: Просвещение, 2003.
2. Алгебра и начала анализа: Учеб. для 10–11 кл. общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н. Колмогорова. – М.: Просвещение, 2004.
3. Алгебра и начала математического анализа. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных . учреждений (профильный уровень)/А.Г. Мордкович и др. ; под редакцией А.Г. Мордковича—7-е изд., стер.—М.: Мнемозина, 2014.
4. Задачи по алгебре и началам анализа: Пособие для учащихся 10–11 кл. общеобразоват. учреждений /С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2003.
10

























