Қысқа мерзімді жоспар №
Сабақ атауы
10 «А» сынып. Алгебра және анализ бастамалары.
Тригонометриялық функциялардың туындысына
есептер шығару.
Сілтеме
Мерсер мен Литлтон /2007/,Александер /2001,2008/ еңбектері, интернет желісі
Жалпы мақсаттар
Тригонометриялық функциялардың туындысына
есептер шығару; оқушылардың логикалық ойлау қабілеттерін дамыту; диалогтік оқыту арқылы сабақтың мазмұнын ашу; формативті бағалауды сыни тұрғыдан ойлау.
Оқыту нәтижелері
- тригонометриялық функциялардың туындысына
есептер шығару.Негізгі білімдерін жинақтау, саралау
-диалогтік әдістің тиімділігін арттыру;
-формативті бағалау әдістерін пайдалануға сенімді болу
Негізгі мақсаттар
1.Білімділік: Оқушылардың туынды, туындыны есептеу
ережелері, күрделі тригонометриялық функциялардың туындысы жөнінде алған
білімдерін тереңдету.
2. Дамытушылық: Ой - өрісін дамыту, ойлау қабілетін арттыру, теориялық білімін практикада қолдана білу дағдысын қалыптастыру.
3. Тәрбиелілік: Шапшаңдыққа, іздемпаздыққа, тиянақтылыққа, ұқыптылыққа
ұжымдық ауызбіршілікке тәрбиелеу.
Сабақ көрнекілігі:
Тест жұмыстары, слайд Microsoft PowerPoint, тілме қағаздар
Сабақ түрі:
топтық және ұжымдық
Сабақты өту әдісі
аралас
Ұйымдастыру кезеңі
J
Ынтымақтастық атмосферасын қалыптастыру.
Жұптастырып жұмыс істеу
Әнгіме: «Ақылдының ақылсыздан парқы»
Негізгі бөлім.
1-тапсырма
Математикалық диктант. Слайд №4
Тұрақтының туындысы Дәрежелік функцияның туындысы Айнымалының туындысы Түбірдің туындысы Бөліндінің туындысы Көбейтіндінің туындысы 2-тапсырма
:
Формулаларды еске түсіреміз
Слайд №5
(sin x)’=cos x
(cos x)’= - sin x
(tg x)’= 1/ cos x
(ctg x)’= -1/ sin x
Механикалық есте сақтау(үнемі қайталап отыру арқалы форлулаларды жаттау. Александр,2001,2008 «нұсқаулық» 51-бет ) Оқушылардың сыни
тұрғыдан ойлауына
әсер ету.
3-тапсырма
6
Бақылау сұрақтары
Слайд №6
1 топтың сурақтары:
y=cosx туындысы неге тең? x² туындысы неге тең? Кері тригонометриялық функцияларды ата. y=sіnx функциясының анықталу облысын айтып бер. y=tgx функциясының туындысы. tg²x+1=? cosx=a түріндегі теңдеудің шешімі. топтың сурақтары: 1. Тұрақты санның туындысы.
2. х-тің туындысы
3. Туындыларды есептеу ережелерінің формуласы.
4. y=ctgx туындысы неге тең?
5. y=cos3x туындысы неге тең?
6. Күрделі функция туындысы неге тең?
7.y=x³+sіnx функциясының туындысы неге тең?
Оқушыларға «туынды» тарауы бойынша бақылау сұрақтарын қоя отырып, олардың тарау бойынша алған білімдерін тексеремін.
Просмотр содержимого документа
«Оңдықтармен және бірліктермен санау»
САБАҚТЫҢ ЖОСПАРЫ
Тақырып: Векторлардың скалярлық көбейтіндісі . 2 сағат.
Білімділік: Векторлық скалярлық көбейтіндісінің анықтамасы,
Дамытушылық: Өтілген тақырып бойынша алған білімдерін есеп шығрағанда қолдана білу қабілеттерін дамыту.
Тәрбиелік: өз бетімен жұмыс істей білуге, шапшаңдыққа, тапқырлыққа тәрбилеу.
Мақсат: Оқулықтағы жаттығуларды орындай алу мақсаты көзделеді.
Құрал-жабдықтар,көрнекті құралдар: сызғыш, сызба плакаттар.
Сабақ түрі: жаңа білім алу сабағы.
Әдіс-тәсілдер: Лекция.
Сабақ барысы
Оқыту үрдісінің маңыздылығы:
1.Ұйымдастыру кезеңі.
2.Үй жұмысын тексеру.
Үйге берліген тапсырманы тақтаға жазғызып талқылау (оқушылар үйден шығара алмаған есептерді)
ДМ.(С тобы) АВС үшбұрышының АД, ВЕ, СҒ медианалары О нүктесінде қиылысады.
Шешуі:
Жаңа тапсырмаларды қалыптастыру:
I. Анықтама.
Яғни, , ( 1) мұндағы
(2)
О
Қасиеттері:
Дәлелдеуі:
ә) Егер
II .
.
III. Теорема: Екі вектордың скалярлық көбейтіндісі олардың сәйкес координаторларының көбейтіндісінің қосындысына тең.
Дәлелдеуі.
*(
(3)
Дербес жағдай:
(4)
Жаңа білімді бекіту: Есептер шығару
№1 Үшбұрыштың А(1;1), В(4;1), С(4;5) төбелері берілген, үшбұрыш бұрыштарының косинусын есептеңдер. (Шәкілікова. Геометрия 9-сынып. №70)
Шешуі: 1.
0 1 4
2.
;
Жауабы: 0;
№2. (Шыныбеков. Геометрия 9-сынып . №121)
Егер
Шешуі:
(
(
Жауабы:
№3. (Шәкілікова. Геометрия 9- сынып №84)
Жауабы.-2. .
Қосымша есептер: №116; №117 (Шыныбеков. 9- сынып)
№116. Егер
№117 . Егер
0
Үйге тапсырма беру: №69, №72, №81. (Шәкілікова. 9- сынып) . 7- жұмыс, 3,4-нұсқа (ДМ). №123. (Шыныбеков).
Өздік жұмысын алу: (ДМ. 7- жұмыс. 1,2 – нұсқа)
Оқушыларды бағалау : жетістіктері мен кемшіліктерін атап айту.
Сабақты қорытындылау: Өтілген тақырыптың негізгі түйінін сұрау.
 теңдігін, векторлардың скалярлық көбейтіндісінің геометриялық мағынасын, векторлардың перпендикулярлық белгісін білу; координаторлары берілген векторлардың скалярлық көбейтіндісін, векторлар арасындағы бұрыштың шамасын таба алу, скалярлық көбейтінді туралы теореманы дәлелдей алу.
теңдігін, векторлардың скалярлық көбейтіндісінің геометриялық мағынасын, векторлардың перпендикулярлық белгісін білу; координаторлары берілген векторлардың скалярлық көбейтіндісін, векторлар арасындағы бұрыштың шамасын таба алу, скалярлық көбейтінді туралы теореманы дәлелдей алу.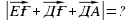 Мұндағы СА
Мұндағы СА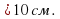
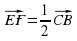 , :
, :  ,
, 

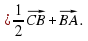
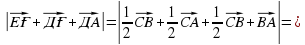
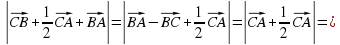

 векторларының скалярлық көбейтіндісі деп осы векторлардың ұзындықтарын олардың арасындағы бұрыштың косинусына көбейткендегі көбейтіндіні айтады. Екі вектордың скалярлық көбейтіндісінің белгіленуі:
векторларының скалярлық көбейтіндісі деп осы векторлардың ұзындықтарын олардың арасындағы бұрыштың косинусына көбейткендегі көбейтіндіні айтады. Екі вектордың скалярлық көбейтіндісінің белгіленуі: 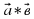 .
.
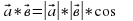 , ( 1) мұндағы
, ( 1) мұндағы 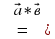 ). 2 сурет
). 2 сурет

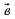
 (2)
(2)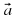 А
А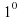 .
. 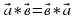 (орын ауыстырымдылық)
(орын ауыстырымдылық) +
+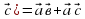 (үлестірімділік заңы)
(үлестірімділік заңы)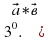 )
) (
( (көбейтіндінің үлестірімділік қасиеті)
(көбейтіндінің үлестірімділік қасиеті) 0, онда
0, онда 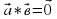
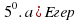
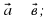 онда
онда 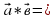 0
0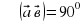 , яғни
, яғни 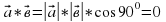
 , (
, ( , бұдан
, бұдан 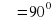 ;
; 
 координаталық вектор.
координаталық вектор. 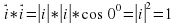
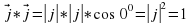 .
.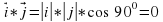
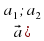 ),
),  ),
), 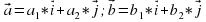
 *(
*( *
*















