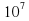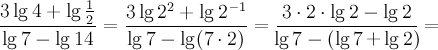Государственное областное бюджетное
профессиональное образовательное учреждение
«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Методическая разработка
урока математики
на тему
«Логарифмические уравнения».
Выполнил:
преподаватель математики
первой квалификационной категории
Заварзина В.Г.
Липецк 2015 г.
Тема урока:
«Логарифмические уравнения».
Цели урока:
1. Образовательные
а) повторить вычисление логарифмов с помощью изученных свойств; закрепить умения решать логарифмические уравнения.
б)сформировать умение использовать полученные теоретические знания для решения практических задач, научиться выстраивать логические умозаключения и делать выводы;
2. Развивающие:
а) развитие профессиональных качеств обучающихся (умений применять полученные знания на практике);
б) развитие познавательных умений и мышления (выделять главное, анализировать, сравнивать, определять и объяснять понятия).
3. Воспитательные:
а)формирование коммуникативных компетенций (умение работать в группе, умение отстаивать свое мнение, умение выслушивать мнение других);
б)воспитание навыков самостоятельной работы;
в) воспитание дисциплинированности.
Задачи урока:
отработка навыка добывания знаний через практическую деятельность;
закрепить навыки работы в группе, умение аргументированно отстаивать свое мнение и вести дискуссию;
формировать навыки освоения учащимися картины мира через изучение нового материала;
Тип урока: комбинированный
Вид урока: урок обобщения и систематизации:
Методические приемы:
-самостоятельная работа (работа с раздаточным материалом);
-практический- решение задач.
Межпредметные связи: история
Оборудование и наглядные средства обучения: рабочие тетради, мультимедийный проектор, интерактивная доска, презентация, демонстрационный и раздаточный материал, задачник “Алгебра и начала математического анализа” (профильный уровень часть1, 2) под редакцией А. Г. Мордковича .
Методическая цель: активизировать мыслительную деятельность обучающихся.
Ход урока:
I.Организационный момент: подготовка учащихся к уроку (проверка отсутствующих на уроке, наличие тетрадей, проверка готовности рабочих мест учащихся и учителя, готовности учащихся к работе.)
На первом этапе учитель приветствует учащихся, проверяет готовность класса к работе.
II. Сообщение темы и целей урока. (слайд 1,2)
Вступительное слово преподавателя.
Добрый день ребята!
Сегодня мы повторим понятие логарифма числа, свойства логарифма, закрепим умения применять эти понятия при решении уравнений. Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех.
Тема урока: “Логарифмические уравнения ”.
Эпиграфом урока являются слова М.В. Ломоносова: (слайд 3)
“Математику уже затем учить надо, что она ум в порядок приводит”.
Цель нашего урока, показать знания определения логарифма, свойств логарифма и уметь применять все ваши знания при решении уравнений.
Для того, чтобы показать свои знания по данной теме, вы должны быть настойчивыми, целеустремленными. Я желаю вам успешной работы и надеюсь, что мы получим удовольствие от сегодняшнего урока.
III. Проверка домашнего задания
Историческая справка (было задано подготовить исторические сведения о логарифмах)
История логарифма.
В конце Средних веков и начале Нового времени математики все чаще стали обращаться к соотношению между геометрической и арифметической прогрессиями. М.Штифель в своем сочинении Арифметика целых чисел (1544) привел таблицу положительных и отрицательных степеней числа 2:
Штифель заметил, что сумма двух чисел в первой строке (строке показателей степени) равна показателю степени двойки, отвечающему произведению двух соответствующих чисел в нижней строке (строке степеней). В связи с этой таблицей Штифель сформулировал четыре правила, эквивалентных четырем современным правилам операций над показателями степеней или четырем правилам действий над логарифмами: сумма в верхней строке соответствует произведению в нижней строке; вычитание в верхней строке соответствует делению в нижней строке; умножение в верхней строке соответствует возведению в степень в нижней строке; деление в верхней строке соответствует извлечению корня в нижней строке.
Приложения логарифмов(слайды 4,5)
Логарифмическая функция возникает в связи с самыми разными природными формами. По логарифмическим спиралям выстраиваются цветки в соцветиях подсолнечника, закручиваются раковины моллюска Nautilus, рога горного барана и клювы попугаев. Все эти природные формы могут служить примерами кривой, известной под названием логарифмической спирали. Такую кривую описывает движущаяся точка, расстояние от полюса которой растет в геометрической прогрессии, а угол, описываемый ее радиусом-вектором – в арифметической. Повсеместность такой кривой, а следовательно и логарифмической функции, хорошо иллюстрируется тем, что она возникает в столь далеких и совершенно различных областях, как контур кулачка-эксцентрика и траектория некоторых насекомых, летящих на свет.
Ребята, давайте проверим домашнее задание.(решение у доски в то время, пока рассказывают историческую справку; с комментарием – обоснованием )
На дом были заданы следующие примеры:
(Проверяем примеры у доски)
№1.
а) log 10 100000 = 5, т.к. 105 = 100000 (определение логарифма и свойства степени),
б) log 5 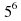 = 6
= 6
в) log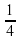 4 = –1, т.к. 4–1 =
4 = –1, т.к. 4–1 = 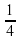 (…).
(…).
№ 2.
1.log6 3 + log6 12.
2.log2 64 – log2 3.
3.log3 405 − log3 5.
IV. Систематизация и обобщение знаний.
Разминка.
Принято, что день обычно начинается с зарядки, а урок с разминки. Проведем разминку и мы.
Ребята, давайте вспомним полученные знания по данной теме и ответим на вопросы. За каждый правильный ответ вы получите жетон и сохраните его до конца урока.
Мы знаем, что слово логарифм происходит от греческого λόγοφ (число) и αρіμοφ (отношение) и переводится как отношение чисел. Это понятие ввел английский математик Джон Непер.
Дайте определение логарифма числа.
Правильные ответы обучающихся:
(Логарифмом положительного числа b по положительному и отличному от 1 основанию a называют показатель степени, в которую нужно возвести число a, чтобы получить число b.) (слайд 6)
Ребята отвечают на вопросы.
1. Дайте определение десятичного логарифма.
2. Перечислите основные свойства логарифмов.
3.Приведите пример для вычисления логарифма. (слайд 7)
4. Вычислите данный логарифм. На доске (log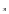 (-5)=; log
(-5)=; log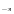 6=)
6=)
5. Какие основные правила используют при вычислении логарифмов?
Ответы обучающихся к заданиям.
1. Логарифм по основанию 10 называют десятичным логарифмом.
2. Основные свойства логарифмов
loga x + loga y = loga (x · y);
loga x − loga y = loga (x : y).
Сумма логарифмов равна логарифму произведения, а разность — логарифму частного.
3. Пример:
lg 10000000=lg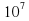 =7
=7
4. log (-5)= решений нет.
(-5)= решений нет.
log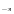 6= решений нет.
6= решений нет.
Данные логарифмы решений не имеют, т.к. отрицательные числа при логарифме и основание быть не могут.
4.
1.loga a = 1 Логарифм по любому основанию a от самого этого основания равен единице.
2.loga 1 = 0 Основание a может быть каким угодно, но если в аргументе стоит единица — логарифм равен нулю! Потому что a0 = 1 — это прямое следствие из определения.
V.Решение примеров у доски.
Давайте решим следующие примеры на доске..
№1
Какими формулами вы воспользуетесь при решении?(слайд 8)
log6 18 + log6 2.
log2 24 − log2 3.
log3 117 − log3 13.
4. Вычислить 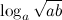 , если
, если 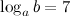
5. Упростить выражение
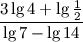
6. Найти значение выражения
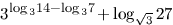
Привожу правильное решение примеров.
log6 18 + log6 2=2.
log2 24 − log2 3=3.
log3 117 − log3 13=2.
1.Найдите значение выражения: log6 18 + log6 2.
Решение
Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log6 18 + log6 2 = log6 (18 · 2) = log6 36 = 2.
Ответ:2
2.Найдите значение выражения: log2 24 − log2 3.
Решение
Основания одинаковые, используем формулу разности:
log2 24 − log2 3 = log2 (24 : 3) = log2 8 = 3.
Ответ:3
3.Найдите значение выражения: log3 117 − log3 13.
Решение
Основания одинаковые, поэтому имеем:
log3 135 − log3 13 = log3 (117 : 13) = log3 9 = 2.
Ответ:2
4. Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:
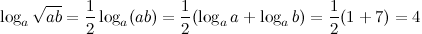
Ответ. 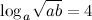
5.Решение Перепишем числитель, используя свойство для степени логарифма, а знаменатель, используя свойство –логарифм произведения:
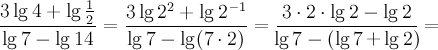
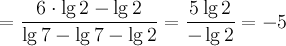
Ответ: 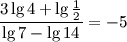
6.Решение:
В степени первого слагаемого разность логарифмов заменим на логарифм частного, а для второго слагаемого применим свойство логарифмов для степени основания: 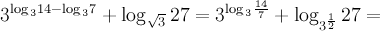
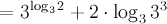
В полученном выражении к первому слагаемому применим основное логарифмическое тождество, а ко второму – свойство логарифма степени
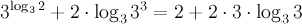
учитывая, что 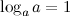 , получим
, получим
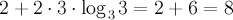
Ответ: 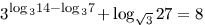
№ 2.(слайды 9)
Решите уравнения:
1)log3 (2х-5) = log3х
ОДЗ: x0;x2,5
Применяем потенцирование, получаем: x0;x.2,5
2х-5 = х
х=5
Ответ: х=5
2)log3 (2х-1) = 2
ОДЗ: x0,5
Исходя из определения логарифма, а именно, что логарифм - это число, в которое надо возвести основание, чтобы получить выражение, которое находится под знаком логарифма, т.е. (4х-1), получаем:
3 2 = 2х-1
2х-1 = 9
х =5
Ответ: х=5
3)Необходимо найти корень уравнения или сумму корней, если их несколько:
log3 (х 2-3) = log3 (2х)
Применяем потенцирование, здесь оно допустимо. В итоге получаем обычное квадратное уравнение.
х 2-3 = 2х
х 2-2х-3 = 0
Находим корни уравнения:
х1= 3
х2= -1
Получилось два корня
Проверим результат и подставим его в исходное уравнение. Начнем с х1= 3:
log36 = log36
Проверка прошла успешно, теперь очередь х2= -1:
log3 (-2) = log3 (-2)- решений нет
Ответ 3.
4)Решите уравнение
log2(5 + 3log2(x - 3)) = 3,
Решение.
a) Логарифмом положительного числа b по основанию a (a 0, a ≠ 1) называется степень, в которую нужно возвести число a, чтобы получить b. Таким образом, logab = c b = ac и, следовательно,
5 + 3log2(x - 3) = 23
или
3log2(x - 3) = 8 - 5, log2(x - 3) = 1.
Опять используя определение, получим
x - 3 = 21, x = 5.
Проверка полученного корня является неотъемлемой частью решения этого уравнения:
log2(5 + 3log2(5 - 3)) = log2(5 + 3log22) = log2(5 + 3) = log28 = 3.
Получим истинное равенство 3 = 3 и, следовательно, x = 5 есть решение исходного уравнения.
Ответ: x = 5
5)Решите уравнение
log(x - 2)9 = 2,
получим уравнение
(x - 2)2 = 9.
Возведя в квадрат, получим квадратное уравнение x2 - 4x - 5 = 0 с решениями x1 = -1 и x2 = 5. После проверки остается лишь x = 5.
Ответ: x = 5
6) Решите уравнение
log3x + log3(x + 3) = log3(x + 24)
Решение. ОДЗ уравнения есть множество x (0;+) которое определяется из системы неравенств (условия существования логарифмов уравнения)
| 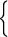
| x 0, |
| x+3 0, |
| x+24 0. |
получим
| log3x + log3(x + 3) = log3(x + 24) |
| | 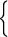
| log3x(x + 3) = log3(x + 24), | | x 0, |
| |
| 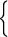 | x(x + 3) = x + 24, | | x 0, |
| | 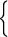 | x2 + 2x - 24 = 0, | | x 0, |
| | 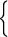 | 
| x1 = -6, | | x2 = 4, | |
| x 0, |
| x = 4. |
Ответ: x=4
VI. Закрепление применения знаний, умений и навыков.
Для достижения поставленной цели урока вам надо показать свои знания. На доске задания для самостоятельной работы по вариантам. Решаете задания на листочках.
I Вариант
1. lg2 x3 - 10lgx + 1=0
2.log х+1(2x2+1)=2
II Вариант
1. X lgх+2= 1000
2. log 5 x=log 5 (6-x2 )
Решение заданий:
I Вариант
1. lg2 x3 - 10lgx + 1=0
Приведём уравнение к квадратному:
Т.к. lg2 x3=(lgx3)2=(3lgx)2= 9lg2 x, то
9lg2 x - 10lgx+1=0.
Пусть lg x=y, тогда 9y2- 10y+1=0; D=64
y=1 или y=1/9
lgx=1 или lgx=1/9
x=10 или х=10 1/9.
Проверкой подтверждаем, что оба числа являются
корнями.
Ответ: 10; 10 1/9
2.log х+1(2x2+1)=2
По определению логарифма имеем: 2х2+1=(х+1)2,
X2 -2x=0
x=2 или x=0.
Проверка:
х=0 не может быть корнем данного уравнения, так как основание логарифма х+1≠1.
При х=2 log 2+1( 2•22 +1)=log39=2.
Ответ: 2.
II Вариант
1. X lgх+2= 1000
Логарифмируя обе части уравнения ( x 0), получим:
( lgx+2)•lgx=lg1000
Lg2 x+ 2lgx- 3=0
lgx=y
у2+ 2у- 3=0
y=- 3, у=1.
lgx=- 3, x=10-3=0,001;
lgx=1, x=10
Выполнив проверку, убедимся, что оба найденных значения переменной являются корнями данного уравнения.
Ответ: 0,001; 10.
2. log 5 x=log 5 (6-x2 )
Из равенства логарифмов следует:
x= 6- x2
x2-x-6=0; D=25
x=-3 или x=2.
Проверка:
x=-3 корнем уравнения быть не может, так как
логарифмы отрицательных чисел не существуют.
Log5 x=log52,
Log5(6-x2) = log5 (6-22)=log5 2.
Ответ: 2.
VII. Подведение итогов урока:
Опрос (1-2 минуты)
1. Одно из решений уравнения. (корень)
2. Результат умножения. (произведение)
3. Число не являющееся ни отрицательным, ни положительным. (нуль)
4. Логарифм произведения равен …(сумме логарифмов)
5. Число, содержащее в записи запятую.(десятичная дробь)
6. Логарифм частного равен …( разности логарифмов)
7. При делении степеней с одинаковыми основаниями показатели …(вычитаются)
Сегодня на уроке мы закрепили навыки решение логарифмических уравнений, вычисления логарифмов, повторили правила вычисления логарифмов с помощью изученных свойств, повторили вычисление десятичных логарифмов.
Выставление оценок за урок.
VIII. Домашнее задание:
§17 №17.8, 17.12(слайд 10)
Список литературы:
1. Выгодский М.Я. Справочник по элементарной математике. — М.: АСТ, 2003.
2. Алгебра и начала анализа: Учеб. для 10–11 кл. общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н. Колмогорова. – М.: Просвещение, 2004.
3. Алгебра и начала математического анализа. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных . учреждений (профильный уровень)/А.Г. Мордкович и др. ; под редакцией А.Г. Мордковича—7-е изд., стер.—М.: Мнемозина, 2010.
4. Алгебра и начала анализа: Учеб. для 10 кл. общеобразоват. учреждений /С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2003.
5. Задачи по алгебре и началам анализа: Пособие для учащихся 10–11 кл. общеобразоват. учреждений /С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2003.
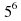 = 6
= 6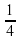 4 = –1, т.к. 4–1 =
4 = –1, т.к. 4–1 =  (-5)=; log
(-5)=; log 6=)
6=)