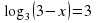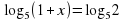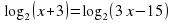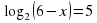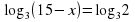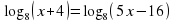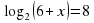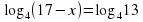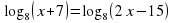| III. Актуализация знаний. Ставит цель занятия перед учащимися. Организует восприятие и осмысление новой информации. Для свободного размышления предлагает ученикам составить «Кластер». Работая в группах, ученики самостоятельно составляют кластер Очень часто приходится решать подобную задачу: известно, что ax=b. Необходимо найти показатель степени х, то есть решать задачу, обратную возведению числа в степень. При нахождении этого показателя степени х и возникает понятие логарифма числа b по основанию а. Обозначается x = logab. Определение логарифма. Определение: Логарифмом числа по основанию называется показатель степени, в которую надо возвести основание а, чтобы получить число b. Это число обозначается символом logab . Из определения следует 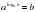 . . Это равенство называется основным логарифмическим тождеством. Операцию нахождения логарифма числа называют логарифмированием
. Объяснение свойств логарифмов (по слайдам презентации)

Рассмотрим основные свойства логарифмов. 1. 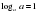 Пример: 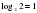 2. 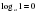 Пример: 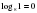 3. 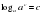 Пример: 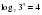 4. Логарифм произведения положительных чисел равен сумме логарифмов множителей. 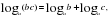 где а 0, а≠ 0, b0,c0. где а 0, а≠ 0, b0,c0. На примере посмотрим ,как применяется данное свойство. 1)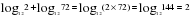 . . 2) 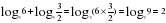 Рассмотрим второе свойство: 5. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. 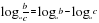 , где a0,a ≠ 0, b0, c 0. , где a0,a ≠ 0, b0, c 0.
Примеры: 1) 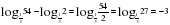 . . 6) 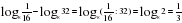 . . 6. Логарифм степени с положительным основанием равен показателю степени, умноженному на логарифм основания. 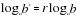 , где a 0, a ≠ 0, b 0 , , где a 0, a ≠ 0, b 0 , 
Задание для группы 1.Записать следующие равенства в виде логарифма: 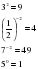 2. Записать следующие равенства в виде показательных: 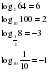 При выполнении задания мы встретились с логарифмом, имеющим основанием число 10. Такие логарифмы называются десятичными и имеют специальное обозначение lg. Например: lg100 = 2, 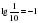 . . 3. Записать числа -3, -1, 0, 1, 3 в виде логарифма с основанием 2. 4. Найдите х: 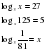
2. Решение задач с целью усвоения свойств логарифма. Найдите значение выражения: 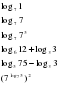 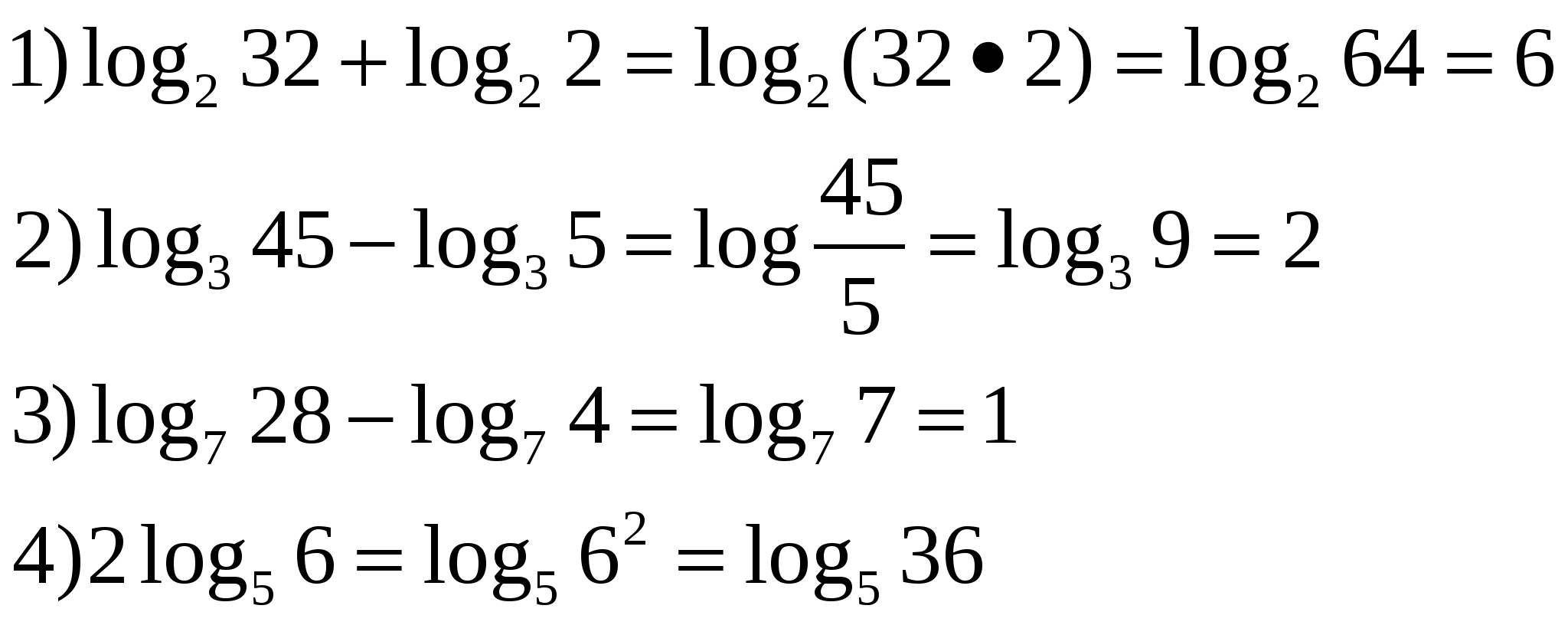
Для тех, кто быстро и верно решает, подготовлены дополнительные задания на карточках: Вычислите: 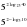 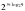 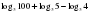 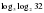 Взаимопроверка (работа в группах по карточкам)
. | 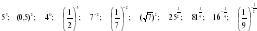
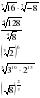
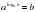 .
. 
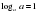
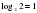
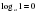
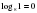
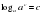
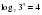
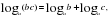 где а 0, а≠ 0, b0,c0.
где а 0, а≠ 0, b0,c0.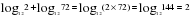 .
.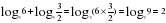
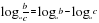 , где a0,a ≠ 0, b0, c 0.
, где a0,a ≠ 0, b0, c 0.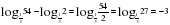 .
.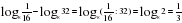 .
.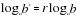 , где a 0, a ≠ 0, b 0 ,
, где a 0, a ≠ 0, b 0 , 
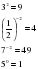
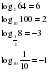
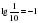 .
.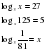
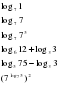
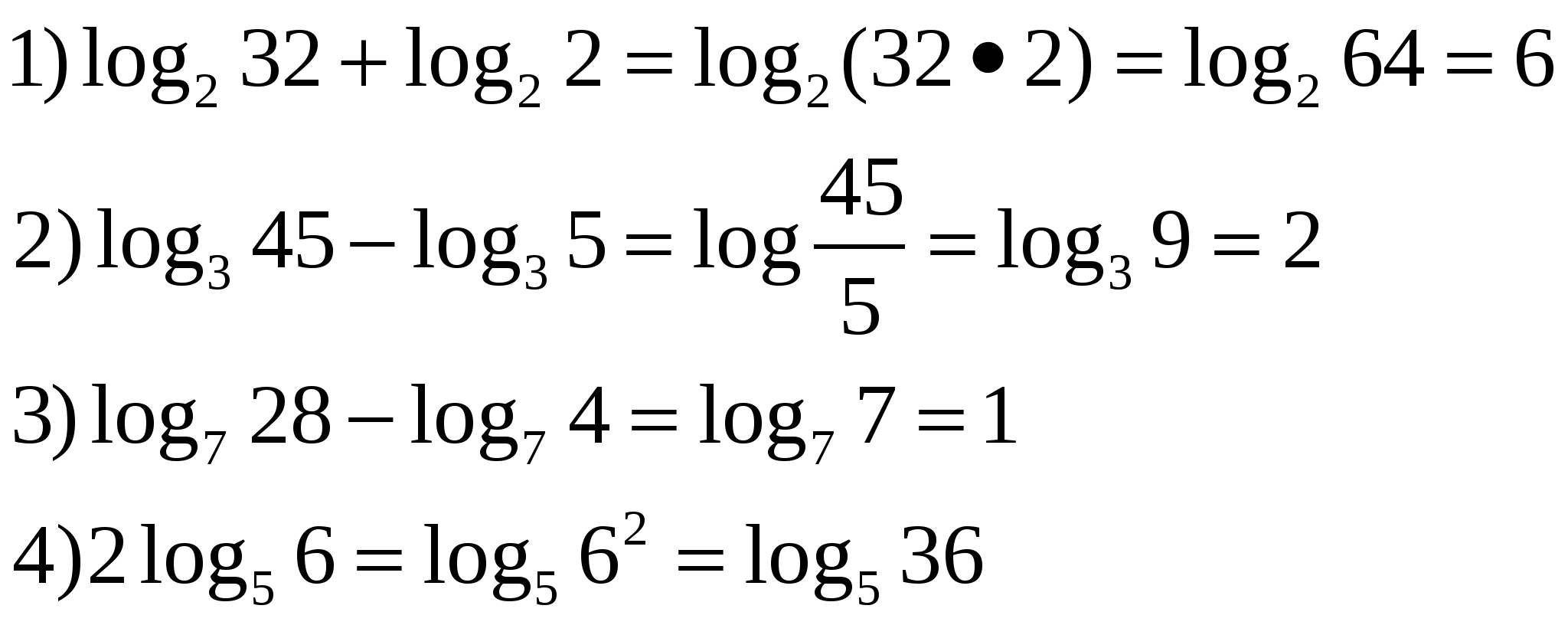
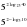
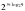
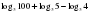
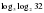
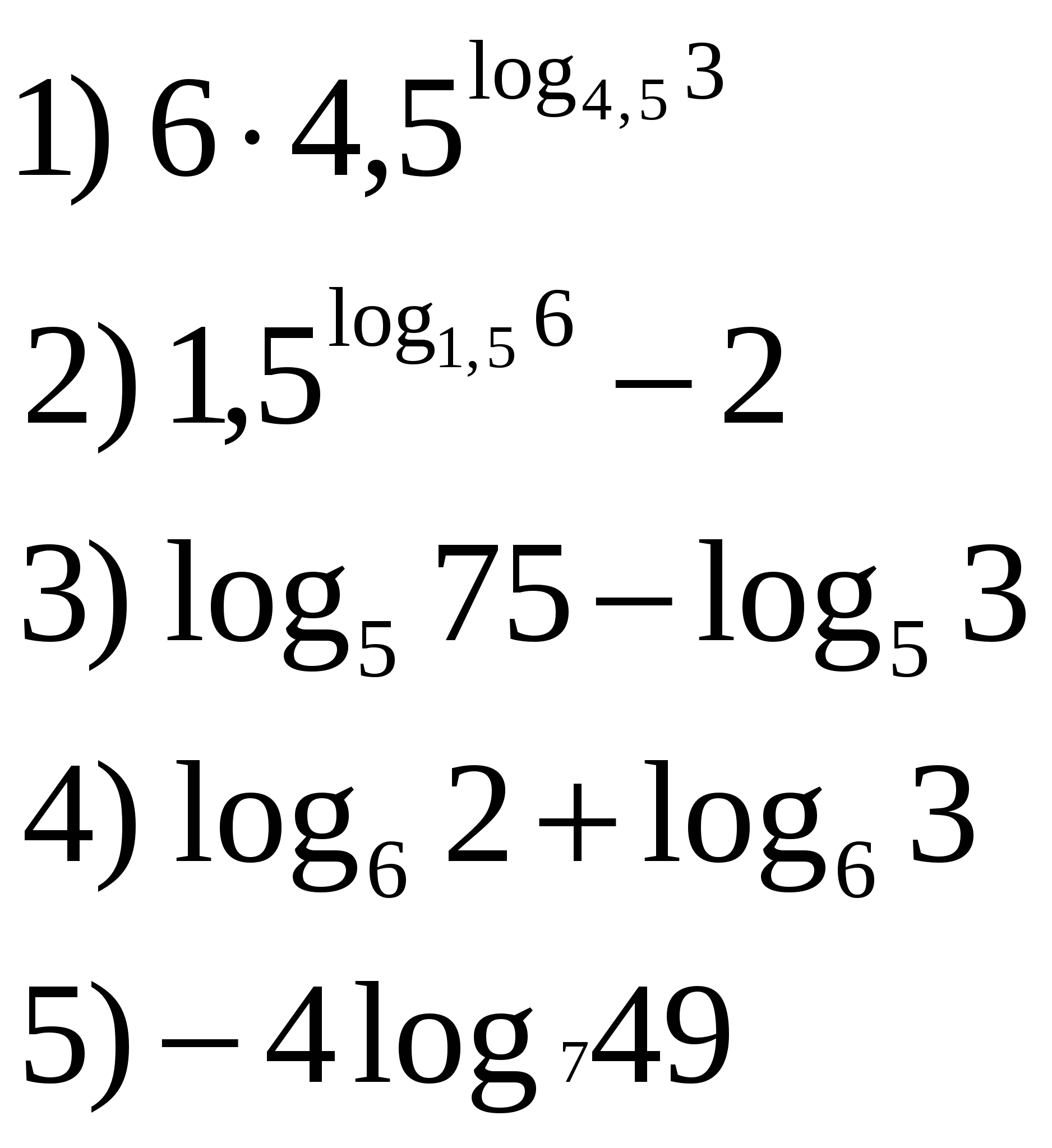
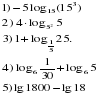
 Ребята, давайте попробуем оценить каждый свою работу за урок.
Ребята, давайте попробуем оценить каждый свою работу за урок. - Кто работал добросовестно – зелёным.
- Кто работал добросовестно – зелёным. - Кто принимал участие в строительстве храма – красным.
- Кто принимал участие в строительстве храма – красным.