Средняя школа № 6
План – конспект открытого урока по математике
в 11 «В» классе
Учитель: Белгибаева Неля Борисовна.
Урок-закрепление:
«Математическое путешествие с логарифмом»
Цели урока:
1.Закрепление определения логарифма, свойств логарифмов, логарифмические уравнения.
2.Развитие умения ориентироваться в нестандартных ситуациях, развитие сообразительности.
3.Привитие навыков групповой работы, формирование чувства коллективизма и преемственности поколения.
4.Знакомство с историческим материалом.
Ход урока:
- Организационный момент.
а)Ребята, здравствуйте!
Сегодня наш урок математики будет несколько необычен. Это будет урок-закрепление по логарифму, который мы назовем «Путешествие с логарифмом».
б)Откройте пожалуйста, ваши тетрадки и зафиксируйте дату путешествия с логарифмом.
Мы должны преодолеть все препятствия-задания и показать, насколько хорошо мы знаем все о логарифме,насколько хорошо мы дружим с ним.
Класс разбивается на 3 группы. В каждой команде выбирается капитан. (Три ряда в классе.Каждый участник имеет рабочую тетрадь, в которой будет записывать по ходу урока примеры и задания. В конце урока эти тетради собираются учителем на проверку).
- Препятствие: ЛОГАРИФМ.
Математика-царица наук,
Арифметика-царица математики.
(К.Гаусс)
1)Вопрос: Дайте определение логарифма данного числа по данному основанию.
(Логарифмом данного числа в по основанию а называется показатель степени,в которую нужно возвести основание а,чтобы получилось число в). (а ?0; а≠1)
2)Вопрос: Каким числом обозначается логарифм числа в по основанию а?
- ав
3)Вопрос: Записать основное логарифмическое тождество.
аlogа в= в,если а ?0; а≠1; в?0.
4)Вопрос: Для обозначения десятичных логарифмов принята специальная запись.Запишите ее.
- 10в=lgв
5)Вопрос: Найти значения(устно):
1) log 232=5
2) log 3243=5
3) log 3 1 =-5
243
4) log 50,04=-2
5) log 3 3=2
6)log 3 1 =-4
9
6)Вопрос: Найдите значение Х(устно):
- log 3 х=1 (х=3) (31 =х)
2)log 5 х=0 (х=1) (х=( 0 =1)
(х=1)
3) log 1 х = 1 (х= 1) (х=( 1) 1 = 1)
8 8 8 8
4) log х 1 =2 (х= 1 ) (х2= 1 )
16 4 16
(х = 1 )
4
5) log х 81=4 (х=3) (х2= 1 )
16
(х = 1 )
4
6) logх 1=1 (х= 1 ) (х1= 1 )
9 9 9
(х= 1 )
9
7) logх 1=0 (х0= 1 х-любое число )
(х0= 1 х-любое число,х>0 )
7) Вопрос: Упростите выражения (устно),пользуясь основным логарифмическим тождеством
[alog aв= b]:
- 1,9 log1,92 =2
- 2 log 25 =5
- 32-log318=1
2
- 6 -2 log65 = 1
25
ІІ). Препятствие: ОСНОВНЫЕ СВОЙСТВА ЛОГАРИФМОВ.
Тот,кто не знает математику,
Не может узнать никакой другой науки.
(Роджер Бэкон)
1)Вопрос: Перечислите и запишите основные свойства логарифмов (при любом а>0; а≠1 и х>0;у>0):
1) logа1=0 3 ученика у доски (І,ІІ,ІІІ ряды пишут)
2) logа а=1
3) logа ху= logа х+ logа у
4) logа х = logа х -logа у
У
5)logа хр = р logа х
2)Вопрос: Запишите формулу перехода от одного основания к другому основанию.
logbX
logа х= ,где (х>0 и а≠1; в>0 и в≠1)
logbX
3)Вопрос: Вычислите:
1) lg8+ lg 125= lg 8 x 125 = lg 1000 = 3
2) log2 11- log 244= log 2 11= log 2 1= log 2 (2) -2= -2
3)lg13+ lg 130=lg 13 = lg 1 = lg 10-1= -1
- 10
4)log3 16 = log 416=2
log3 4
5)log 12 4+ log 1236= log 12(4х36) = log 12 144=2
6) log 1 1 =0
2
7) log 71/2=1
ІІІ). Препятствие: ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ.
Математика-точильный камень способностей.
1)Вопрос: Дать определение логарифмической функции:
(функцию,заданную формулой
у=logа х,
называют логарифмической функцией с основанием а).
2)Основные свойства логарифмической функции:
1.Область определения логарифмической функции-множество всех положительных чисел Ft,т.е.
Д(logа) =Ft
2.Область значений логарифмической функции –множество всех действительных чисел.
3.Логарифмическая функция на всей области определения возрастает
(при а>1) или убывает (при 0<а<1).
3).Вопрос: Построить графики функций у=logа b:
- y
у=logа х
b
0 1 abx
(а>0)
ІІ) y
у=logа х
0 1 abx
(0<а<1) b
ІІІ)
у
у=logа х
b
0 1 abx
(а>1)
4)Вопрос: Найдите область определения функции:
f(х) =log8 (4-5х)
Решение: 4-5х>0
-5х >-4
х <0,8
ответ: х€(-∞;0,8).
5)Вопрос:Сравните числа:
1) log 2 9,9 и (>)log 2 9,3
2) log 34,9 и (<)log 2 5,1
3) log 0,2 1,9 и (>) log 0,2 2,3
4) log1/3 0,51 и (<)log1/3 0,49
5) log 3 и (>) 1=log
ІV).Препятствие: ЛОГАРИФИЧЕСКИЕ УРАВНЕНИЯ.
Математика черпает свою силу в умении исключать все лишнее в процессе мышления.
(Э.Мах)
1)Вопрос: Решите уравнение:
log3 (2х-1) =2
log3 (2х-1) =log3 9
2х-1=9
2х=9+1
х=10:2
х=5
Ответ: х=5
2)Вопрос: Решите уравнение:
xlogx10=5x
10=5x
х=10:5
х=2
Ответ: х=2
3)Вопрос:Решите уравнение:
log7 (8х-17) =1
log7 (8х-17) =log7 7
8х-17=7
8х=7+17
8х=24
х=24:8
х=3
Ответ: х=3
4)Вопрос:Решите уравнение:
3х= 1
27
3х=3-3
х=-3
Ответ: х=-3
5)Решите уравнение:
logх-1 4=2
х=3
Ответ: х=3
V).Препятствие: СВЕДЕНИЯ ИЗ ИСТОРИИ.

 7) logх 1=0 (х0= 1 х-любое число )
7) logх 1=0 (х0= 1 х-любое число )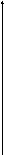




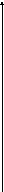
 у
у