|
1. | Организационный момент Организация психологического настроя | - Проведем небольшой тест, который называется «Психогеометрия». Перед вами 5 фигур, посмотрите внимательно, выберите какая вам больше всего нравиться? У каждой фигуры есть свой номер, покажите на пальцах номер понравившейся вам фигуры.
Оказывается, каждая фигура символизирует ваши личностные качества. Сейчас мы посмотрим, какие.
1.Квадрат – вы трудолюбивы; 2. Зигзаг – самый восторженный знак и способен увлечь за собой многих. 3. Круг – самый доброжелательный из 5 фигур. Способностью сопереживать и сочувствовать. 4. Треугольник – вы лидеры, энергичные и неудержимые личности; 5. Прямоугольник – ваши ведущие качества любознательность, интерес ко всему происходящему, смелость.
- Будем надеяться, что, так или иначе, все эти качества помогут вам сегодня.
| Мобилизуют внимание, настраиваются на урок.
Выбирают понравившуюся геометрическую фигуру (фигуры на столах)
|
«Психогеометрия» |
| 2. | Актуализация знаний | - Ещё в глубокой древности было подмечено, что некоторые многочлены можно умножить короче, быстрее, чем все остальные. Так появились формулы сокращенного умножения, их несколько. Сегодня мы с вами в роли исследователей «откроем» ещё две из этих формул. - Начать наше занятие мне бы хотелось со слов замечательной женщины - великого математика Софьи Васильевны Ковалевской “ У математиков существует свой язык- это формулы”. (эпиграф урока на слайде)
- Давайте поставим цели урока.
«Проверь себя» Тест№1
Математический диктант
Письменно: Найдите квадраты выражений: c; -4: 3m; 5x2y3; -7cy6. Найдите произведение: 3x и 6у; 2m и -3m2; 7a и 5b. 3) Чему равно удвоенное произведение этих выражений? 4) Выполните умножение: (х+6)(х-5).
|
Постановка целей урока. (Узнаем формулы сокращённого умножения, научимся их записывать, читать, проговаривать и пользоваться ими.)
(Ответ: чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить) Самопроверка (Ответ: c2; 16; 9m2; 25x4y6; 49c2y12.) (Ответы: 18xy; -6m3; 35ab.)
(Ответы: 36xy; -12m3; 70ab.)
(Ответ: х2-5х+6х-30 = х2+х-30.)
|
Фронтальная работа
Индивидуальная форма работы |
|
3. | Изучение нового материала | Обьяснение нового материала
Работа по группам: Работаю с таблицами (у каждой группы в таблице свои 3 примера)
Объединитесь в группы; Выберите старшего; Получите задание, оно соответствует номеру группы; Выполните умножение двучленов. Озвучьте (старший группы) и сравните свой результат
- Ребята, посмотрите. Есть ли что-то общее в условиях и ответах предложенных упражнений?
- Итак, мы открыли формулу квадрат суммы двух выражений: (а + b)2 = а2 + 2аb + b2 Правила сокращенного умножения Совместное обсуждение. В чем отличие от результатов первых вычислений
- Итак, мы открыли вторую формулу сокращенного умножения - формулу квадрат разности двух выражений: (а - b)2 = а2 - 2аb + b2.
Обобщение учителя: Равенство (1) – квадрат суммы, Равенство (2) – квадрат разности – называются формулами сокращенного умножения. И применяются для упрощения вычислений. Эти формулы можно читать как слева направо, так и справа налево, при чтении справа налево многочлены а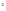 +2аb+b +2аb+b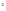 и а и а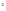 -2аb+b -2аb+b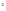 в виде произведения одинаковых множителей (а+b) или (а-b). в виде произведения одинаковых множителей (а+b) или (а-b). Историческая справка - Первые общие утверждения о тождественных преобразованиях встречаются у древнегреческих математиков, начиная с шестого века до н.э. Среди математиков Древней Греции было принято выражать все алгебраические утверждения в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, произведение двух чисел истолковывали как площадь прямоугольника. Отказ от геометрической трактовки наметился у Диофанта Александрийского, жившего в 3 веке. В его работах появляются зачатки буквенной символики и специальных обозначений. Формулы квадрата суммы и разности двух выражений знали еще в Древнем Вавилоне, а древнегреческие математики знали ее геометрическое истолкование, продолжение на слайде Сообщение о Евклиде и доказательство формулы учениками (1 доказывает сумму, обращает внимание на разность) № 347; № 348 - А поможет нам в этом Евклид - ….ученый А при чем здесь он? Да потому что, что он первый вывел доказательство этой формулы геометрическим путем. Перед Вами квадрат, сторона которого равна а.
|
Решают. Анализируют.
Ответы: - Да, во всех случаях результатом умножения служит трехчлен, у которого первый член – квадрат первого слагаемого, второй – удвоенное произведение первого и второго слагаемого, третий – квадрат второго слагаемого. - Новые произведения отличаются от ранее записанных - знаком перед удвоенным произведением
| Групповая работа
|
|
5. | Закрепление | - Чтобы знания можно было эффективно применить, нужно, чтобы они были прочно усвоены. Древняя китайская мудрость гласит: “Я слышу - я забываю, я вижу – я запоминаю, я делаю – я понимаю”
1) Устно найди ошибку (m+n)2 = m2 + mn + n2, (2 + х)2 = 4 + 4х + х2, (1 +р)2 = 12+р2, (2m + 5n)2 = 2m2+20mn + 10n2.
2) Самостоятельная работа в группах. А) Преобразовать выражение в многочлен стандартного вида. (У каждой группы своя карточка)    1 группа 2 группа 1 группа 2 группа
(х-4а)2= (k+2f) 2= (3х+1)2= (d-5g) 2= В) Вычислите 4а2+4ав+в2= 4р2-4ар+а2= 36р2-12рх2+х4= в2+2с2в+с4=
Закрепление материала. Тест№2
|
Фронтальная работа
Групповая работа
Самопроверка
Самопроверка самостоятельная работа |
«Лови ошибку»
«Каждый учит каждого»
Самопроверка Проверочная работа с целью последующей коррекции знаний.
Индивидуальная форма работы
|
|
6. | Рефлексия |
Ян Амос Каменский сказал: «Считай несчастным тот день и час, в который ты не усвоил ничего нового и не прибавил к своим знаниям» -А что прибавили вы? -Чему вы научились на уроке? -Что удалось? -Над чем надо работать?
-Выберите утверждение, которое соответствовало вашему настроению на уроке
|
Проводят рефлексию, анализируют содержание урока.
|
Подведение итогов
|
 +2аb+b
+2аb+b

 1 группа 2 группа
1 группа 2 группа 
















