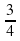Открытый урок обобщения и систематизации знаний по теме «Производная и ее геометрический смысл»
Цели урока:
¨ дидактическая – формирование умений анализировать проблему и планировать способы ее решения; применять знания в новой ситуации, осуществлять исследовательскую деятельность, анализировать, делать выводы;
¨ развивающая – развитие интереса к предмету и наблюдательности, учить видеть связь между математикой, другими науками и окружающей жизнью, развивать грамотную математическую речь;
¨ воспитательная – формирование умения работать самостоятельно и в коллективе; воспитывать волю и настойчивость для достижения конечных результатов.
Задачи для учителя:
- проконтролировать знания правил дифференцирования, основных формул для нахождения производных элементарных функций, уравнения касательной к графику функции;
- проверить навыки по применению своих знаний в ходе решения нестандартных задач;
- развить представления учащихся об использовании знаний по нахождению производной в окружающей их жизни и в других научных областях;
- продолжить работу над развитием логического мышления, умением анализировать, сопоставлять и обобщать полученные знания, проводить исследовательскую работу, результатом которой должен быть мини-проект.
Задачи для учащихся:
1. Знать формулы для вычисления производных элементарных и сложных функций, уравнение касательной.
3. Уметь находить производные функций и уравнение касательной к графику функции.
4. Уметь применять знания на практике в различных науках.
Форма работы: индивидуальная, фронтальная, групповая.
Метод урока: поисково-исследовательский
Тип урока: урок обобщения и систематизации знаний по теме «Производная и ее геометрический смысл» с применением элементов метода проектов и ИКТ.
Ход урока
Организационный момент
Добрый день, друзья! Рада вас видеть. Я желаю вам сегодня на уроке удачи, точных расчетов и вычислений, новых открытий. И ответьте, пожалуйста, на мой первый вопрос: «Какую тему мы изучаем?» («Производная и ее геометрический смысл»)
Сегодня мы с вами продолжим знакомство с производными функций, вспомним и обобщим все те знания, которые вы получили на предыдущих уроках, получим новые знания. Откройте тетради и запишите тему урока:
" Производная и ее геометрический смысл". (слайд 1,2)
Девизом нашего урока по-прежнему остается "Я знаю, что я умею делать. Я знаю, как это сделать", а эпиграфом возьмем замечательные строки поэта А.Поупа:
«Был этот мир глубокой тьмой окутан.
Да будет свет! И вот явился Ньютон».
Догадались, почему? (слайд 3)
Великий английский физик, математик и астроном Исаак Ньютон в конце 12 века ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Для того, чтобы включиться в работу и сконцентрироваться, предлагаю вам небольшую разминку.
Работа устно (слайд 4)
Вопросы:
1. Сформулируйте определение производной функции в точке
2. Сформулируйте правила дифференцирования суммы, произведения и частного
3. Назовите производные элементарных функций
4. В чем заключается механический смысл производной?
5. В чем заключается геометрический смысл производной?
6. Запишите уравнение касательной к графику функции в заданной точке?
Найти производную функции: (слайд 5)
а) y=5x6 -3x4 +2x3-7
б) y= 7sinx –e2x +3x
в) у=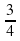
x4 +ln x
Найти значение производной функции y(x) = x2 – 3x в точке с абсциссой x0 = 1
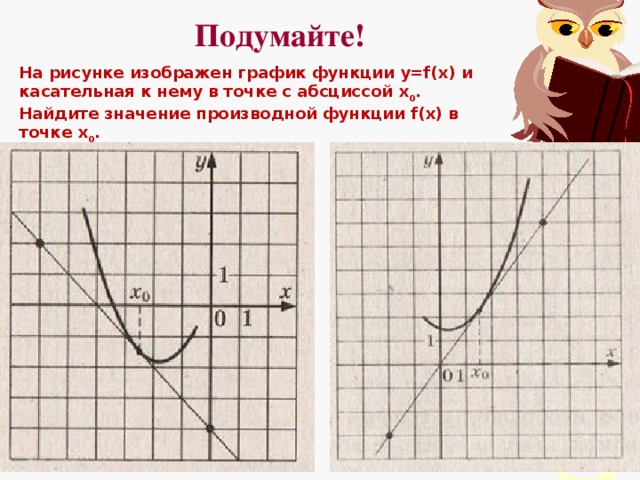
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0. (слайд 6)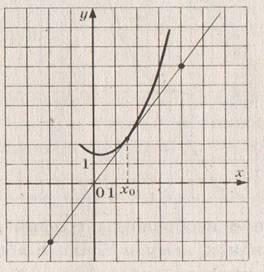
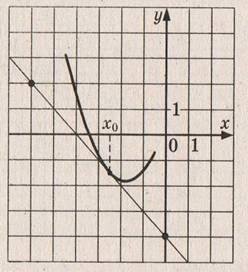
а) tgα=6/6=1, при этом прямая с положительным направлением оси Ох составляет тупой угол, тогда ответ берется со знаком минус
Ответ: -1б) tgα=6/4=1.5, при этом прямая с положительным направлением оси Ох составляет острый угол, тогда ответ берется со знаком плюс.
Ответ: 1,5
Работа у доски (в тетрадях)(слайд 7)
Напишите уравнение касательной к графику функции f(x) = sin 2x - ln(x +1) в точке с абсциссой х0 = 0.
Решение.
y=f(x0)+ f' '(x0)(x-x0), уравнение касательной к графику функции
f( x0) = sin2×0 - ln(0 +1) =0, f' '(x0) = 2 - 1=1
f' '(х) = 2 cos2x - , у = 0 +1(х - 1)
у = х-1 уравнение касательной к графику функции.
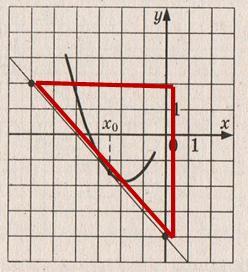
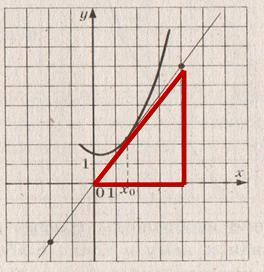
Прямая касается гиперболы у=4/х в точке (1;4). Найти площадь треугольника, ограниченного этой касательной и осями координат.
Решение:
Запишем уравнение касательной к графику функции у=4/х в точке (1;4).
у(1)=4
у`(х)= -4/х2
у`(1)= -4
т.к. y=f(x0)+ f' '(x0)(x-x0), то у=4-4(х-1) и у=8-4х . Прямая у = 8 -4х пересекает оси координат в в точках(0;8) и (2;0), получается прямоугольный треугольник с катетами 2 и8 . S = ٠2٠8 =8(кв.ед).
Производная – одно из фундаментальных понятий математики. Мы изучаем ее в школе.
ПОСТАНОВКА ПРОБЛЕМЫ
Но я уверена, что кто-то из вас подумал: « А зачем изучать её? Пригодятся ли полученные знания по нахождению производных в будущей профессии?»
ВЫДВИЖЕНИЕ ГИПОТЕЗЫ
« Знания по теме «Производная» необходимы в жизни»
ДОКАЗАТЕЛЬСТВО ГИПОТЕЗЫ
Давайте проведем исследование, в результате которого либо подтвердим, либо опровергнем данную гипотезу.
Начнем с прошлого.
Историческая справка
Первую задачу, для решения которой нужно было в древности применить знания по теме «Производная» , называют «Задача Дидоны». Она так названа по имени легендарной основательницы города Карфаген и её первой жрицы. Согласно легенде, вынужденная бежать из своего родного города, Дидона вместе со своими спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей землю для нового поселения. Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитроумная Дидона разрезала воловью шкуру на узкие ремешки и, разложив их, сумела ограничить гораздо большую площадь по сравнению с той, которую можно было покрыть одной воловьей шкурой.
Как видите, решение задач на нахождение наиболее выгодных условий занимали умы людей с древних времен. Но только с появлением дифференциального исчисления был найден метод, позволяющий решать эти задачи по единой схеме, которую мы с вами изучим чуть позже.
Получается, наши предшественники обходились без умения находить производную, но не все же были такими, как Дидона. А вот если бы в то время были школы и изучалась сегодняшняя тема урока, то всем было бы намного легче завоевать большие участки земли.
Настоящее время ( хотя бы сдать хорошо ЕГЭ !)
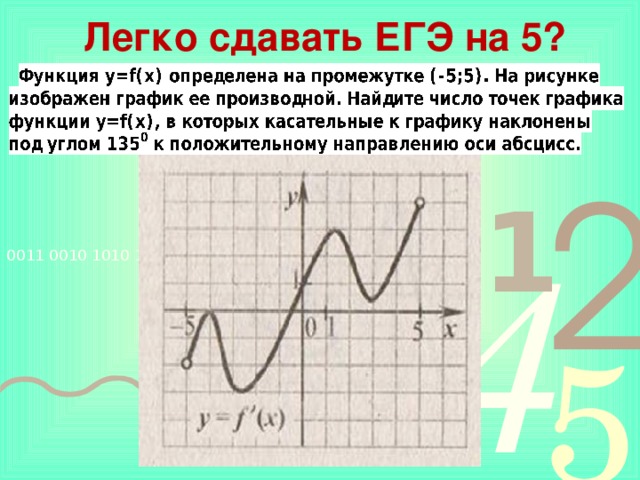
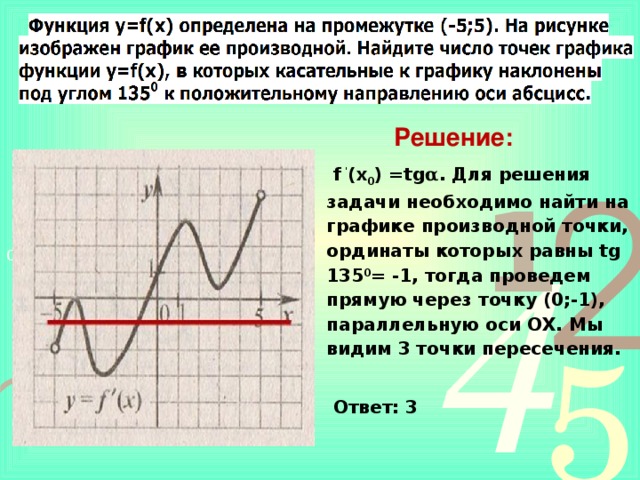
Функция y=f(x) определена на промежутке (-5;5). На рисунке изображен график ее производной. Найдите число точек графика функции y=f(x), в которых касательные к графику наклонены под углом 1350 к положительному направлению оси абсцисс.
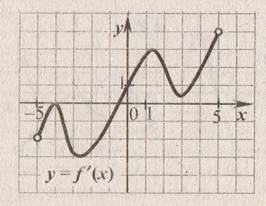
Решение:
f '(х0) =tgα. Для решения задачи необходимо найти на графике производной точки, ординаты которых равны tg 1350= -1. Тогда проведем прямую через точку (0;-1), параллельную оси ОХ. Число точек пересечения равно 3.
Ответ: 3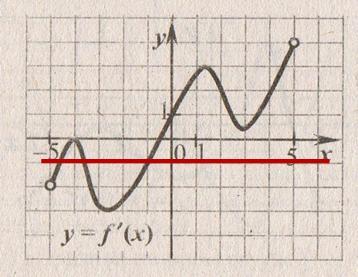
В будущем? В выбранных вами профессиях?
Задача по биологии: По известной зависимости численности популяции x (t) определить относительный прирост в момент времени t. (слайд 9)
Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.
Задача по химии: (слайды 10,11)
Задача по географии: (слайды 12,13)
Задача по экономике: (слайды 14,15)
Вывод: Знания по теме «Производная необходимы, чтобы в будущем быть конкурентноспособной, уважаемой личностью в обществе. (слайд 16)
Домашнее задание: 1 группа подбирает задачи по теме «Производная», связанные с вашей будущей профессией; 2 группа – на основе материала создает либо буклет, либо презентацию. Выбранный вами из класса учащийся будет этот проект защищать.(слайд 17)
Итог урока
- Ребята, что нового вы узнали на уроке?
- Что можно сказать об изменениях, происшедших в вашей учебной деятельности?
Рефлексия
|
|
| Музыка может возвышать или умиротворять душу, Живопись – радовать глаз, Поэзия – пробуждать чувства, Философия – удовлетворять потребности разума, Инженерное дело – совершенствовать материальную сторону жизни людей, А математика способна достичь всех этих целей. Спасибо за урок! (слайд 18) |
