| 3.
4.
5.
6. | Определение цели урока. Цель, которая должна быть достигнута учащимися: - определение цели урока. Цель, которую учитель хочет достичь на данном этапе: - создание условий, позволяющих обучающимся определить цель урока. Задачи: - с помощью проблемной ситуации подвести обучающихся к пониманию необходимости изучения теоремы Пифагора Методы: проблемно-поисковый, работа в парах.
Изучение новой темы. Цель, которая должна быть достигнута учащимися: - изучить формулировку теоремы Пифагора, её доказательство Цель, которую учитель хочет достичь на данном этапе: - создание условий, позволяющих обучающимся изучить формулировку теоремы Пифагора, запомнить её доказательство, познакомиться с исторической справкой. Задачи: - познакомить обучающихся с историей изучения теоремы Пифагора; - сформулировать теорему Пифагора; - оказать помощь обучающимся при доказательстве теоремы. Методы: демонстрация, рассказ, комментирование.
Закрепление учебного материала Цель, которая должна быть достигнута учащимися: -повторить теоретический материал, уметь применять теорему Пифагора к решению задач.
Цель, которую учитель хочет достичь на данном этапе: - создание условий и различных этапов работы для успешной реализации и применения знаний и умений обучающихся; - показать практическое применение изученной теоремы.
Методы: самостоятельная работа, тренировочные упражнения, беседа, фронтальный опрос, наглядные методы.
Рефлексия. Итог урока. Цель: осознание учащимися своих достижений, самооценка результатов деятельности своей и класса. Методы: рефлексивная беседа.
| Создание проблемной ситуации. 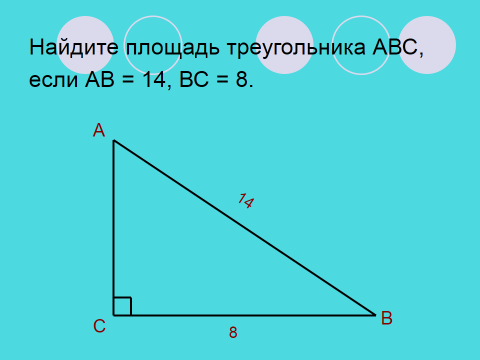 Давайте попробуем решить первую домашнюю задачу, изменив в ней только одно условие. Подумайте над решением вместе со своим соседом по парте (работа в парах). ( Слайд 5) Давайте попробуем решить первую домашнюю задачу, изменив в ней только одно условие. Подумайте над решением вместе со своим соседом по парте (работа в парах). ( Слайд 5)
Обучающиеся приходят к выводу, что основываясь только на тех знаниях, которые у них были до сегодняшнего урока, эту задачу решить нельзя. Делают вывод: чтобы найти катет АС, необходимо знать что-то новое. Исходя из темы урока, предполагают, что это теорема Пифагора, формулируют цель: изучить теорему и научиться применять её к решению задач.
Изучение нового материала разделено на 3 этапа. Историческая справка. (Слайды 6 – 9 ) Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Как всякий отец, Мнесарх мечтал, что сын будет продолжать его дело — ремесло золотых дел мастера. Жизнь рассудила иначе. Будущий великий математик и философ уже в детстве обнаружил большие способности к наукам. Пифагору приписывается изучение свойств целых чисел и пропорций, доказательство теоремы Пифагора и др. Пифагор - это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор - "убеждающий речью".) Своими речами приобрёл 2000 учеников, которые вместе со своими семьями образовали школу-государство, где действовали законы и правила Пифагора. Школа Пифагора, или, как ее еще называют, пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством. Излюбленной геометрической фигурой пифагорейцев была пентаграмма, называемая также пифагорейской звездой. Пифагорейцы пользовались этой фигурой, вычерчивая ее на песке, чтобы приветствовать и узнавать друг друга. Пентаграмма служила им паролем и была символом здоровья и счастья. Несомненно, школа Пифагора сыграла большую роль в усовершенствовании научных методов разрешения математических проблем: в математику твердо вошло положение о необходимости строгих доказательств, что и придало ей значение особой науки. Предание гласит, что когда Пифагор пришёл к теореме, носящей его имя, он принёс богам в жертву 100 быков. В пятисотых годах до нашей эры Пифагор был убит в уличной схватке во время народного восстания. В настоящее время известно около 200 доказательств теоремы Пифагора.  
Формулировки теоремы (Слайд 10) У Евклида эта теорема гласит (перевод): "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол". В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так: "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу". В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол". 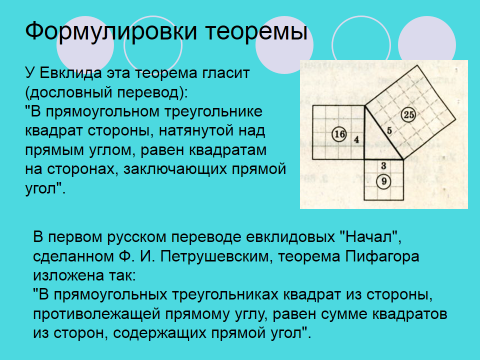 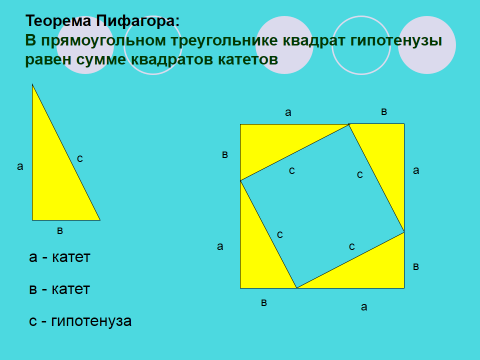
Доказательство теоремы. (Слайды 11,12) Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Достроим прямоугольник до квадрата со стороной a + b.
 Ребята с помощью учителя по чертежу доказывают теорему, затем записывают доказательство в тетради, проводится проверка результатов с помощью компьютерной презентации. Ребята с помощью учителя по чертежу доказывают теорему, затем записывают доказательство в тетради, проводится проверка результатов с помощью компьютерной презентации.
Доказательство: 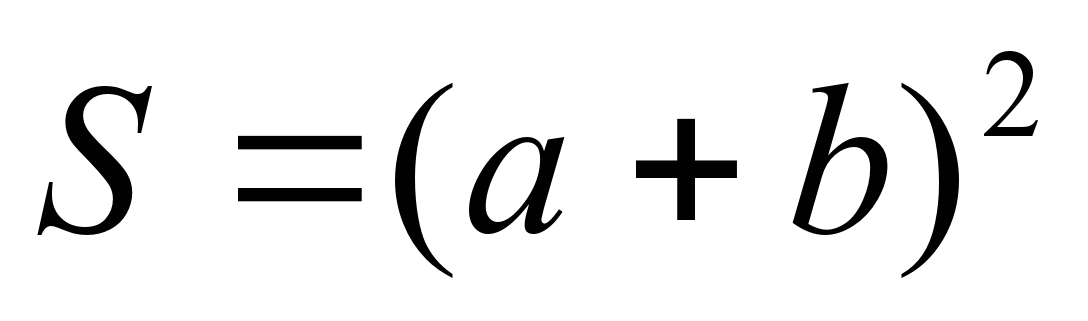 - площадь квадрата - площадь квадрата
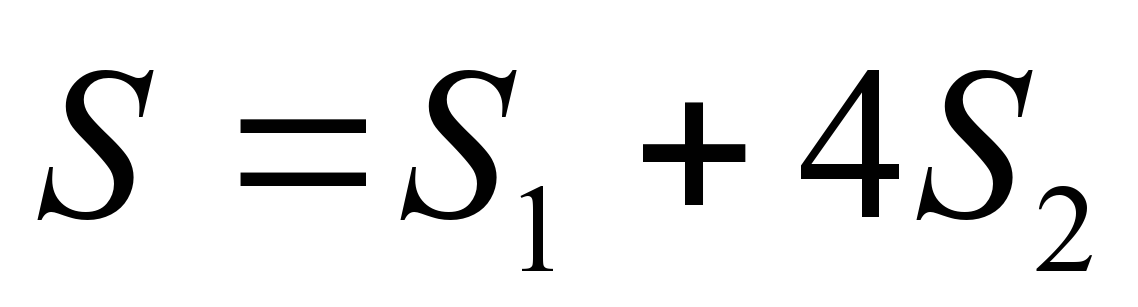
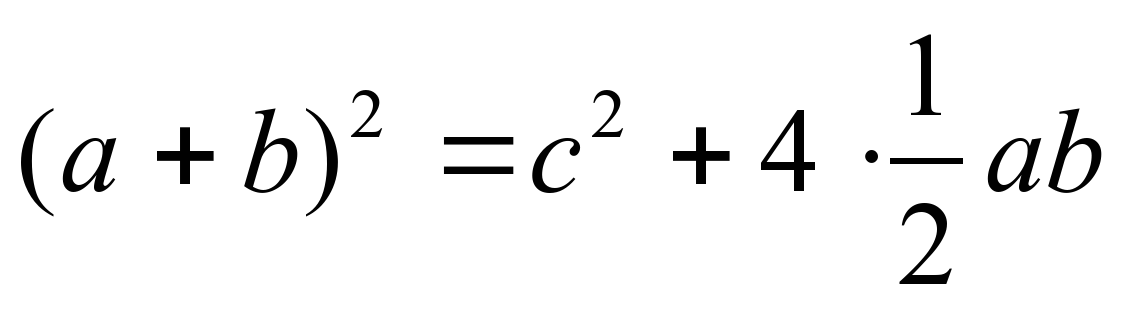
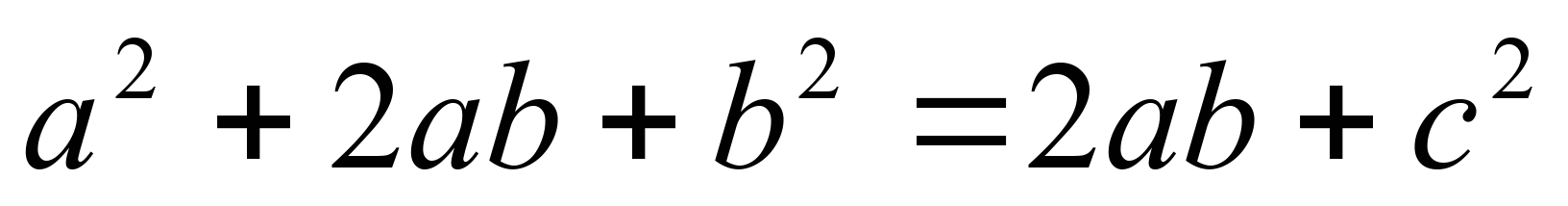
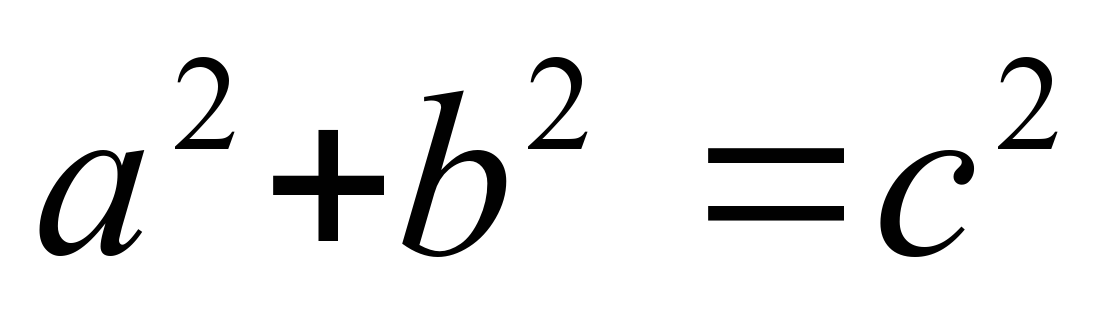 - теорема доказана. - теорема доказана.
Закрепление изученного разделено на два этапа. 1. Первичное закрепление знаний. Работа по учебнику (Применение теоремы Пифагора к решению задач). № 483 (б) – решается у доски и в тетрадях. № 484 (а) – самостоятельная работа с последующей проверкой. После решения задач учитель просит сделать вывод: какие задачи можно решать с помощью теоремы Пифагора? (Слайд 13) Вывод: с помощью теоремы Пифагора можно решать два вида задач: 1) Найти гипотенузу прямоугольного треугольника, если известны катеты. 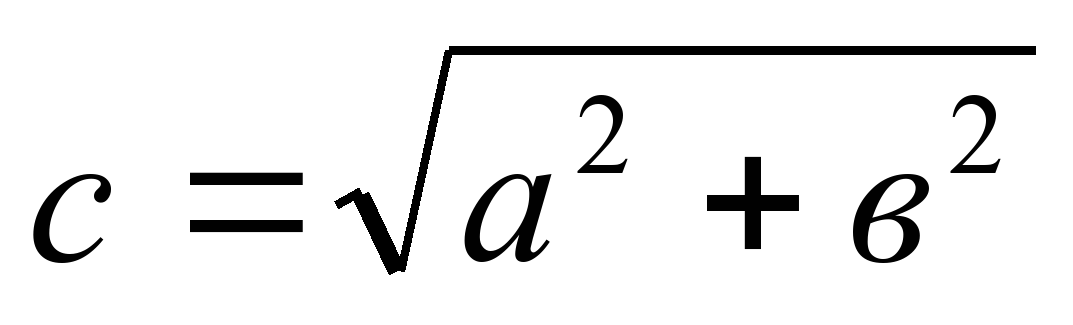
 2) Найти катет, если известна гипотенуза и другой катет. 2) Найти катет, если известна гипотенуза и другой катет.
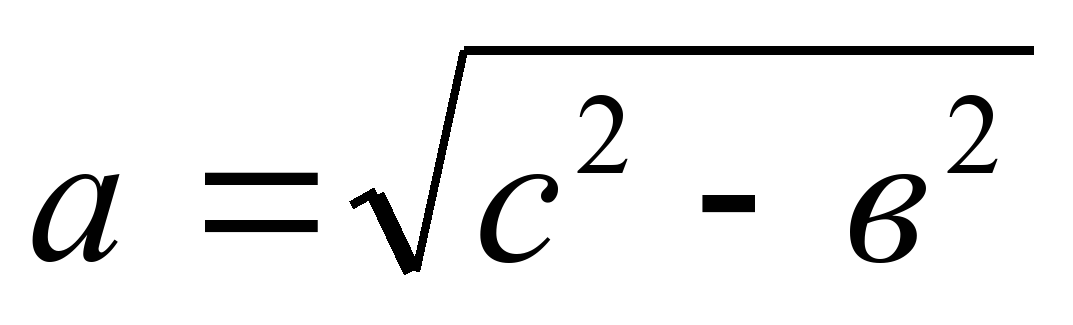
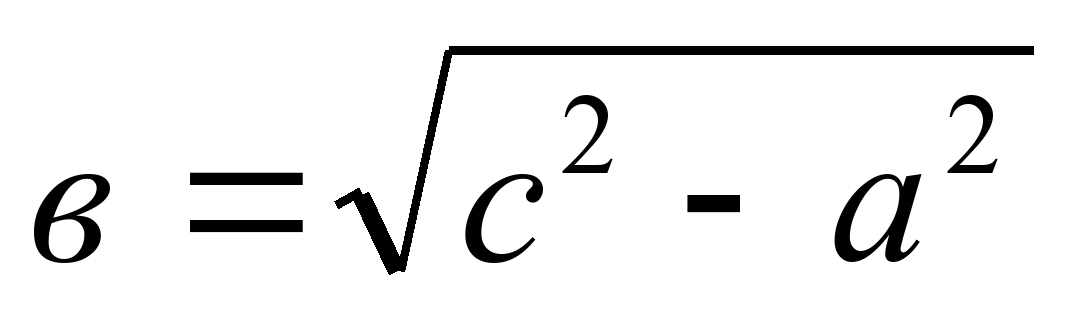 . .
5. Решение задачи практического характера. (Слайд 14) Задача о мобильной связи. В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например радиусе R=200 км, если известно, что радиус Земли равен 6380 км.) Решение: Пусть AB= x, BC=R=200 км, OC= r =6380 км. OB = OA + AB OB = r + x 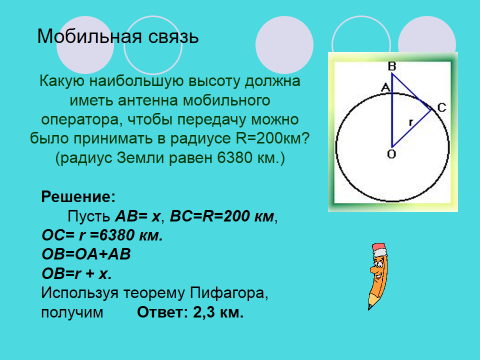 Используя теорему Пифагора, получим ответ. Используя теорему Пифагора, получим ответ.
Ответ: 2,3 км.
Итог урока. Учитель проводит рефлексивную беседу, просит ответить на вопросы. (Слайд 15) Что нового вы узнали сегодня на уроке? Для каких треугольников применяется теорема Пифагора? В чём заключается смысл теоремы Пифагора? 
|

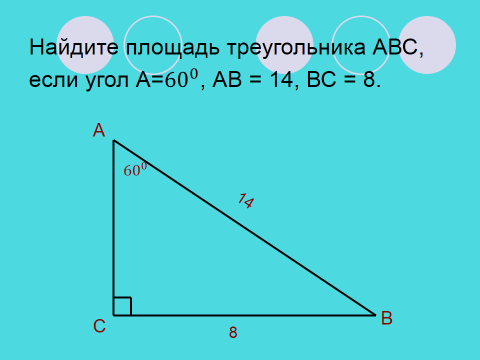

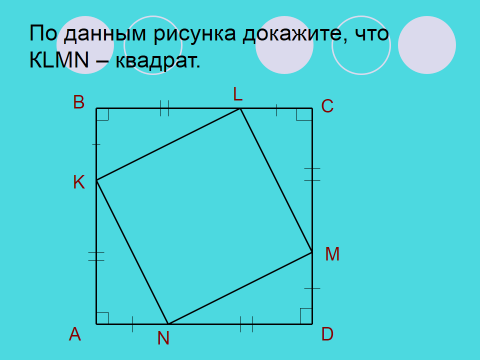
 Давайте попробуем решить первую домашнюю задачу, изменив в ней только одно условие. Подумайте над решением вместе со своим соседом по парте (работа в парах). ( Слайд 5)
Давайте попробуем решить первую домашнюю задачу, изменив в ней только одно условие. Подумайте над решением вместе со своим соседом по парте (работа в парах). ( Слайд 5)





 Ребята с помощью учителя по чертежу доказывают теорему, затем записывают доказательство в тетради, проводится проверка результатов с помощью компьютерной презентации.
Ребята с помощью учителя по чертежу доказывают теорему, затем записывают доказательство в тетради, проводится проверка результатов с помощью компьютерной презентации. 2) Найти катет, если известна гипотенуза и другой катет.
2) Найти катет, если известна гипотенуза и другой катет. Используя теорему Пифагора, получим ответ.
Используя теорему Пифагора, получим ответ. 

















