Конспект урока по геометрии в 9классе
на тему «Длина окружности».
Тема: Длина окружности.
1.Цель урока: Дать представление о длине окружности ;вывести формулу ,выражающую длину окружности через радиус; вести формулу для вычисления длины дуги окружности с градусной мерой угла.
Задачи:
- обучающие: отработать навыки применения полученных формул при решении задач;
-развивающие: активизация мыслительной деятельности учащихся, развитие познавательного интереса к предмету;
-воспитательные: воспитывать аккуратность при работе в тетрадях, формировать навыки самостоятельной деятельности, воспитывать культуру общения, умение работать в коллективе.
Тип урока: комбинированный
Формы работы учащихся: фронтальная работа, индивидуальная,
Необходимое техническое оборудование: компьютер, проектор, набор ЦОРов из Единой коллекции ЦОР и ФЦИОР.
Структура и ход урока
1.Организация учащихся.
Доклад дежурных об отсутствующих.
2 Актуализация знаний учащихся с целью повторения и подведения к восприятию новых знаний.( фронтальная беседа с учащимися): (презентация ПОВТОРЯЕМ ГЕОМЕТРИЮ)
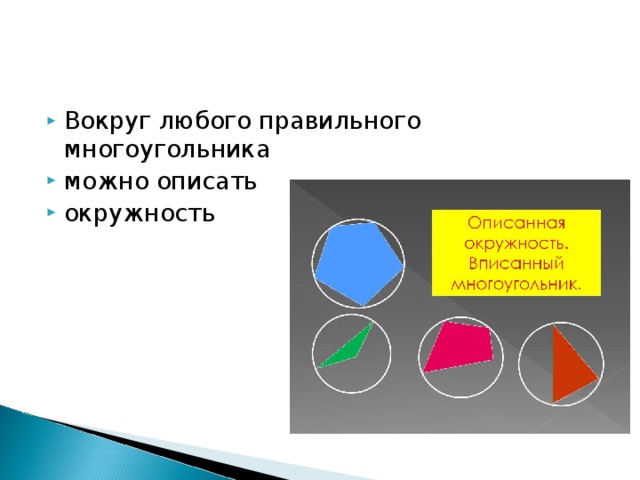
-Какой многоугольник называется правильным?
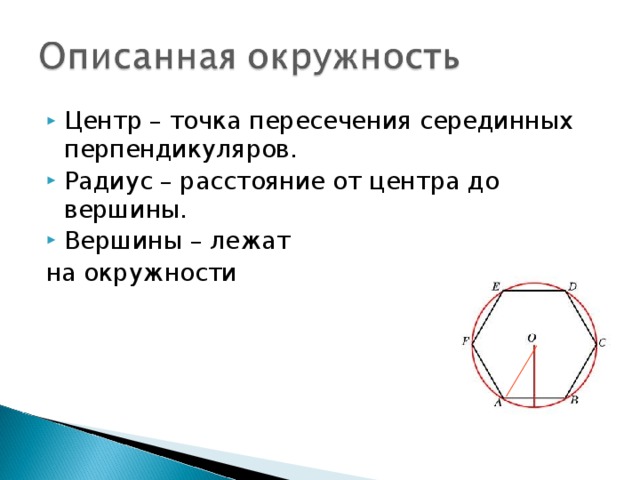
- Какая окружность называется вписанной? Описанной?
-Что называется радиусом окружности?
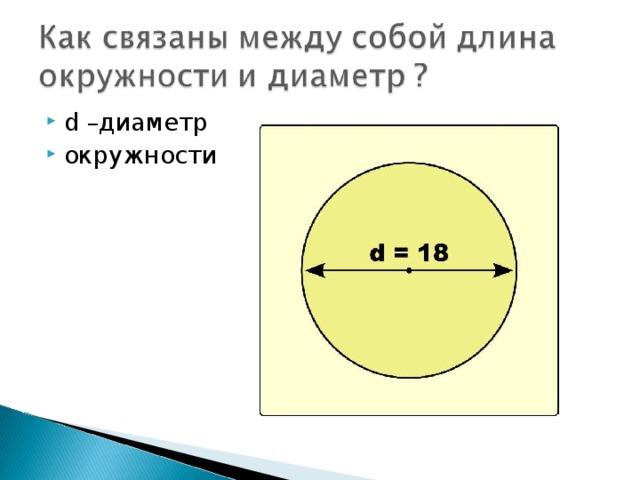
- Что называется диаметром окружности?
- 3.Проверка домашнего задания.
1)Задачи №1098 и №110.
Как связаны радиус окружности и диаметр?(результаты практической работы)
- три предмета: измерить ниткой длину окружности, диаметр найти отношение длины окружности к диаметру.
Вывод из практической работы. Отношение длины окружности к диаметру есть число постоянное и оно было названо π (историческая справка о числе )
На сегодняшнем уроке мы получим формулы для вычисления длины окружности и длины дуги. Итак тема урока: «ДЛИНА ОКРУЖНОСТИ.ДЛИНА ДУГИ»
4. Изучение нового материала.
1. (презентация) « Длина окружности».
1. Длина окружности
Презентация ( прослушивание учащимися ) запись в тетради.
2. Вывод формулы для вычисления длины l дуги с градусной мерой α.
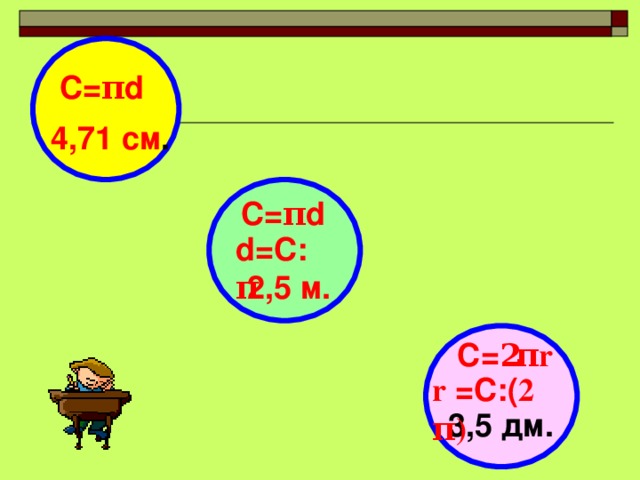
Длина окружности С = 2πR
Длина дуги в 1 градус l = πR /180
Длина дуги в α l = πR /180 * α.
5.Первичное применение новых знаний.(закрепление изученного)
1. Ответить на вопрос?
- как изменится длина окружности, если радиус окружности :
а) увеличить в 3 раза; б) уменьшить в 2 раза?
- Как изменится радиус окружности, если длину окружности : а) увеличить в 2 раза, уменьшить в 3раза?
Решить:
А)Найти длину окружности, если ее радиус равен 12см.(7,5см)
Б) Найти длину дуги окружности радиуса 12см, если градусная мера дуги составляет 30 градусов.(6,28 см)
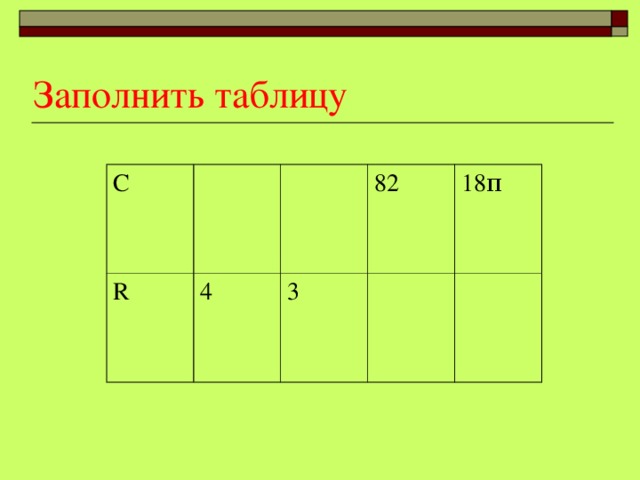
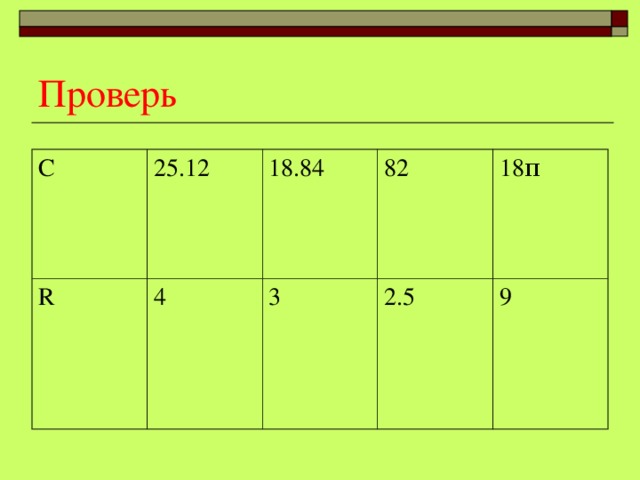
2 Самостоятельно решить задачи ( Презентация « Решить задачи») .
Индивидуальное задание для слабых учащихся (карточки)
6.Обобщение
Что узнали нового?
Связь длины окружности и с радиусом и диаметром.
Формула длины дуги.
7. Задание на дом . п 110
№1109
1108
8.Рефлексия
Просмотр содержимого документа
« КОНСПЕКТ урока по теме ДЛИНА ОКРУЖНОСТИ»
Конспект урока по геометрии в 9классе
на тему «Длина окружности».
Тема: Длина окружности.
Цель урока: Дать представление о длине окружности ;вывести формулу ,выражающую длину окружности через радиус; вести формулу для вычисления длины дуги окружности с градусной мерой угла.
Задачи:
- обучающие: отработать навыки применения полученных формул при решении задач;
-развивающие: активизация мыслительной деятельности учащихся, развитие познавательного интереса к предмету;
-воспитательные: воспитывать аккуратность при работе в тетрадях, формировать навыки самостоятельной деятельности, воспитывать культуру общения, умение работать в коллективе.
Тип урока: комбинированный
Формы работы учащихся: фронтальная работа, индивидуальная,
Необходимое техническое оборудование: компьютер, проектор, набор ЦОРов из Единой коллекции ЦОР и ФЦИОР.
Структура и ход урока
Организация учащихся.
Доклад дежурных об отсутствующих.
2 Актуализация знаний учащихся с целью повторения и подведения к восприятию новых знаний.( фронтальная беседа с учащимися): (презентация ПОВТОРЯЕМ ГЕОМЕТРИЮ)
-Какой многоугольник называется правильным?
- Какая окружность называется вписанной? Описанной?
-Что называется радиусом окружности?
- Что называется диаметром окружности?
- 3.Проверка домашнего задания.
1)Задачи №1098 и №110.
Как связаны радиус окружности и диаметр?(результаты практической работы)
- три предмета: измерить ниткой длину окружности, диаметр найти отношение длины окружности к диаметру.
Вывод из практической работы. Отношение длины окружности к диаметру есть число постоянное и оно было названо π (историческая справка о числе )
На сегодняшнем уроке мы получим формулы для вычисления длины окружности и длины дуги. Итак тема урока: «ДЛИНА ОКРУЖНОСТИ.ДЛИНА ДУГИ»
4. Изучение нового материала.
1. (презентация) « Длина окружности».
Презентация ( прослушивание учащимися ) запись в тетради.
2. Вывод формулы для вычисления длины l дуги с градусной мерой α.
Длина окружности С = 2πR
Длина дуги в 1 градус l = πR /180
Длина дуги в α l = πR /180 * α.
5.Первичное применение новых знаний.(закрепление изученного)
1. Ответить на вопрос?
- как изменится длина окружности, если радиус окружности :
а) увеличить в 3 раза; б) уменьшить в 2 раза?
- Как изменится радиус окружности, если длину окружности : а) увеличить в 2 раза, уменьшить в 3раза?
Решить:
А)Найти длину окружности, если ее радиус равен 12см.(7,5см)
Б) Найти длину дуги окружности радиуса 12см, если градусная мера дуги составляет 30 градусов.(6,28 см)
2 Самостоятельно решить задачи ( Презентация « Решить задачи») .
Индивидуальное задание для слабых учащихся (карточки)
6.Обобщение
Что узнали нового?
Связь длины окружности и с радиусом и диаметром.
Формула длины дуги.
7. Задание на дом . п 110
№1109
1108
8.Рефлексия
Просмотр содержимого документа
«Лист самоконтроля»
Просмотр содержимого презентации
«Решить задачиПрезентация»
Просмотр содержимого презентации
«Тема УРОКА»