Конспект урока математики: "Длина окружности и площадь круга".

Автор Козлова Елена Юрьевна

Учитель математики

Тема урока «Длина окружности и площадь круга»

Учебно-методическое обеспечение: учебник Математика, 6 класс , Н.Я. Виленкин , В.И.Жохов и др.

Цели урока:

Образовательная:

вспомнить понятия окружности и круга; познакомить учащихся с формулами длины окружности и площади круга; учить применять их при решении задач.

Развивающая:

развивать познавательный интерес, творческие способности, выработать самооценку в выборе пути, критерии оценки своей работы, формировать положительный мотив учения, развивать учебно-познавательную активность учащихся, смекалку. Развивать вычислительные навыки и математическую речь.

Воспитательная:

воспитание трудолюбия, взаимопомощи, математической культуры.

Тип урока: комбинированный урок.

Оборудование: мультимедийный проектор; ноутбук; презентация .

Методы обучения: словесный, наглядный, практический, проблемный

Формы работы: индивидуальная, фронтальная, групповая.

Структура урока:

1.Этап «Вызов»

• Мотивационная беседа, с последующей постановкой цели урока .

• Входной контроль – проверка домашнего задания, проверка знаний и умений по пройденному материалу в форме игровых действий, в процессе которых происходит актуализация опорных знаний.

2. Этап «Осмысление»

• Изложение нового материала, в процессе которого раскрывается познавательное содержание; происходит воспроизведение и коррекция учебных знаний.

3. Этап «Рефлексия»

• Первичное закрепление изученного - решение задач познавательного содержания.

4. Этап «Домашнее задание»

• Подведение итогов урока и постановка домашнего задания.

Ход урока

Вызов.

1. Организационный момент.

Прозвенел и смолк звонок,

Всех позвал он на урок.

Актуализация.

В Древней Греции круг и окружность считались венцом совершенства. В русском языке слово круглый тоже может означать высокую степень чего-либо. Вы, наверное, слышали выражения круглый отличник, круглый сирота и даже круглый дурак.

В 5 классе мы познакомились с понятиями окружности и круга.

Прием кластер.

Давайте составим кластер. Каждому ученику заранее раздается бланк Smart Art . Посмотрите на рисунок расположенный в центре и скажите, какие слова или предложения вам приходят на ум в связи с данным рисунком. Потом заслушиваются ответы, составляется общий кластер.

1. Проверка домашнего задания.

1) Вычеркните термины, не имеющие отношения к окружности и кругу.

Прямая; угол; дуга; хорда; треугольник; центр; прямоугольник; радиус; отрезок; диаметр.

Большая часть употребляемых в наше время математических терминов сложилась еще в Древней Греции. Например, «диаметр» от греческого diametros – поперечник.… Еще вавилоняне и древние индийцы считали самым важным элементом окружности радиус. Латинское слово radius и означает «спица колеса», «луч». Термин «радиус» впервые встречается в «Геометрии» (1569 г.) французского ученого П. Рамуса, а затем у Ф. Виета.

2) Разгадайте кроссворд, используя чертежи.

На столе каждого ученика бланки с кроссвордами.

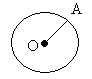
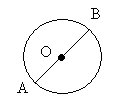
1)OA-… 2)O- … 3)… 4)AB-… 5)…

6) Название инструмента для вычерчивания окружностей.

Прочитайте слово, получившееся в выделенном столбце кроссворда.

Сектор – часть круга, ограниченного двумя радиусами.

3) Итак, закрепим понятия связанные с окружностью и кругом в виде небольшого блиц – опроса.

• 1. Замкнутая линия, все точки которой лежат на одинаковом расстоянии от данной точки плоскости, называется...........................................................

• 2. Окружность можно построить с помощью..............................................

• 3. Часть плоскости, ограниченная окружностью, называется ..................

• 4. Точка внутри круга, от которой равноудалены все точки окружности, называется ..................................................................................................

• 5. Отрезок, соединяющий две любые точки окружности, называется……………………………………………………………….

• 6. Отрезок, соединяющий центр с любой точкой окружности, называется …………………………………………………………………………….

• 7. Отрезок, соединяющий две любые точки окружности и проходящий через центр, называется………………………………………………………….

• 8. Диаметр (больше, меньше) радиуса в …………………………….. раз.

• 9. Часть окружности, ограниченная двумя точками, называется...............

• 10. Диаметр делит круг на два........................................................................

• 11. Часть круга, ограниченная двумя радиусами называется……………….

Осмысление.

1. Объяснение нового материала.

Как вы думаете, что такое длина окружности?

1) Возьмем круглый стакан, поставим на лист бумаги и обведем его карандашом. На бумаге получится окружность. Если «опоясать» стакан ниткой, а потом распрямить ее, то длина нитки будет приближенно равна длине нарисованной на листе окружности.

2)Длина окружности тем больше, чем больше ее диаметр. Длина окружности прямо пропорциональна длине ее диаметра. Поэтому для всех окружностей отношение длины окружности к длине ее диаметра является одним и тем же числом.

Это отношение обозначают греческой буквой .

3) Впервые вычисление числа , обозначающего отношение дли­ны окружности к ее диаметру, на основе теоретических рас­суждений предпринял Архимед (287-212 г.г. до н. э.). Он установил, что . В Китае во второй половине V в. ученый Цзу - Чунчжи получил для приближение 3,1415929... Это прибли­жение дает ошибку лишь в седьмом десятичном знаке.

В своей книге «Об измерении окружности» (1424 г.) ал-Каши нашел для значение с 16 верными знаками. Оно далеко превос­ходило по точности все ранее известные. Пользуясь методом высшей математики, Л. Эйлер вычислил с точностью до 153 десятичных знаков. После опубликования его работы стало общепринятым обозначение (первая буква в греч. слове «пери­ферия» — круг), которое встречается впервые у английского математика У. Джонса.

Точное значение числа вычислить невозможно. По мере развития математики и вычислительной техники появляется возможность установить его с большей точностью. Современное значение числа выглядит так:

В практических расчетах часто пользуются приближенным значением числа с точностью до сотых .

4) Если длину окружности обозначить буквой С, а диаметр – буквой d , то или .

Так как , то формула длины окружности.

5) Устная работа.

Вычислите длину окружности, радиус которой 1 см; 10 см; 1000 см; 1 м; 2 дм.

1. Физкультминутка.

Глазки видят всё вокруг,

Обведу я ими круг.

Глазком видеть всё дано-

Где окно, а где кино.

Влево вправо посмотрю,

Плечиками покручу

Обведу я ими круг,

Погляжу на мир вокруг.

6) Площадь круга.

Существует легенда о финикийской царевне Дидоне, которая, спасаясь от своего брата тирана, доплыла до Африки, где и захотела купить небольшой участок земли. Нумидийский царь согласился продать ей землю, но за огромные деньги и такой крохотный клочок, который она смогла бы окружить ремнем из одной бычьей шкуры. Царевна блестяще справилась с этой задачей, которую в ее честь с тех пор стали называть задачей Дидоны. Как вы думаете, как она это сделала? Она разрезала бычью шкуру так, что получился тонкий кожаный ремешок, которым она и окружила большой кусок земли. Вообще-то это задача математическая. Она формулируется так: «Какую наибольшую площадь можно окружить веревкой заданной длины?»

Возьмем веревочку и свяжем ее в кольцо. Положив полученное кольцо на плоскость, сделаем из него разные фигуры: квадрат, треугольник, окружность и т. д. Площадь, ограниченная окружностью, (КРУГ) - наибольшая среди полученных таким образом площадей.

Круг – плоская фигура, его характеризует площадь.

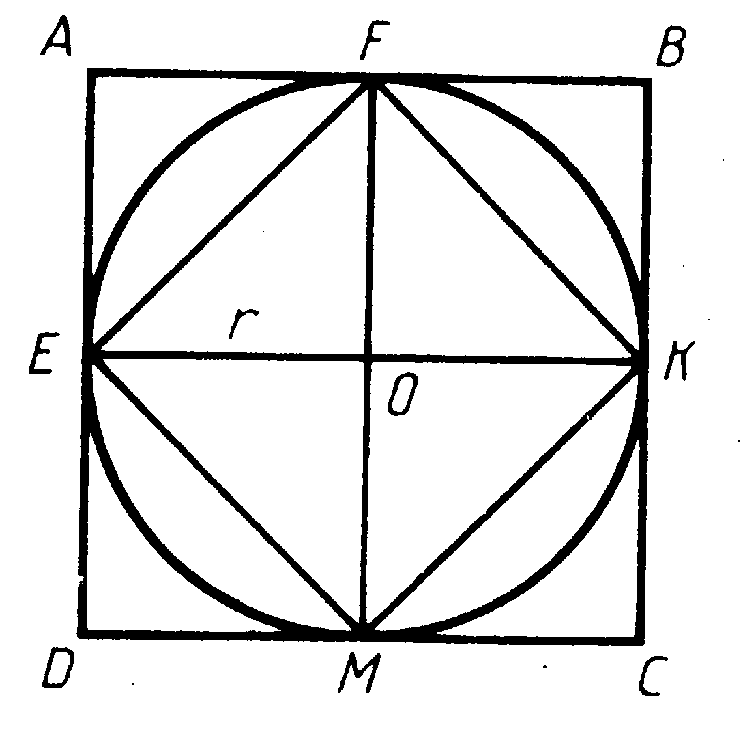
На рисунке изображены круг и два квадрата ADCD и EFKM. радиус круга равен r, поэтому длина стороны квадрата ABCD равна 2r, а его площадь 4r ² . Площадь треугольника EOF вдвое меньше площади квадрата AEOF, поэтому площадь EFKM вдвое меньше площади квадрата ABCD, т.е. равна 2r ². Площадь круга S больше площади квадрата EFKM, но меньше площади квадрата ABCD:

.

Примерно площадь круга равна 3r ². Можно доказать, что

7) Устная работа.

Вычислить площадь круга, диаметр которого равен 2 см; 20 см; 0,2 см.

Рефлексия.

1. Первичное закрепление изученного материала.

Решите задачи.

1) Ныне самым старым деревом является гигантский кипарис, который растет на кладбище с селе Санта-Мария-де-Туле вблизи города Оахака (Южная Мексика). Диаметр ствола этого дерева 16 м. 28 человек, взявшись за руки, еле могут обхватить его. Как считают специалисты, возраст его не меньше 5 000 лет. Вычисли длину обхвата дерева и площадь его поперечного сечения. Число округли до единиц.

2)

У Лукоморья дуб зеленый;

Златая цепь на дубе том:

И днем и ночью кот ученый

Все ходит по цепи кругом…

А.С.Пушкин

Какова была длина цепи, обвитой вокруг дуба один раз, если кот шел со скоростью 0,35 км/ч в течение шести часов и прошел 70 кругов? Найдите диаметр этого дуба и площадь его сечения. Число округлите до целых.

1. Домашнее задание.

1. П. 24, № №867,868,869,883.

2. Написать синквейн на тему: «Окружность и круг».

1. Итог урока.

Окружность как совершенная геометрическая форма всегда привлекала к себе внимание художников и архитекторов.

Назовите архитектурные памятники , которые вы видите на фото, а также имена тех, кто их создал.

В неповторимом архитектурном облике Санкт–Петербурга восторг и удивление вызывает «чугунное кружево» - садовые ограды, перила мостов и набережных, балконные решетки и фонари. Особую воздушность придают воротам окружности, сплетенные в орнамент.

Торжественность и устремленность ввысь зданий достигается использованием арок, представляющих дуги окружностей.

Архитектура Православных церквей как обязательные элементы включает в себя купола, арки, округлые своды, что зрительно увеличивает пространство, создает эффект полета, легкости.

Все это придает особое очарование нашему городу.

На этом наш урок закончен. Вы все были внимательны и активны. Благодарю вас за работу.

Технология развития критического мышления – это технология организации учебного и воспитательного процесса, которая применима к любой программе и любому предмету. Она формирует культуру сотрудничества, культуру работы с информацией, развитие критической позиции как по отношению к окружающему миру, так и по отношению к себе, формирует «человека думающего».
Применяя в своей практике данную технологию, я рассчитываю сделать обучение более эффективным в плане пробуждения интереса к предмету, критического осмысления учениками получаемой в процессе обучения и жизненного опыта информации, осознанной работы с изучаемым материалом, умения обобщать, проводить рефлексию своей деятельности, подводить итоги. В выступлении показаны различные приёмы, используемые на уроках математики на стадиях вызова, осмысления и рефлексии, раскрыты уроки некоторых типов, предлагаемых

Я проводила комбинированный урок с использованием информационно-коммуникативных технологий – сделала презентацию. Также использовала такие методы обучения, как игровая ситуация, методики критического мышления, прием организации индивидуальной и групповой работы учащихся на начальной стадии урока, когда идет актуализация имеющегося у них опыта и знаний. Он позволяет выяснить все, что знают или думают ученики по обсуждаемой теме. Прием «Составление кластера». Смысл этого приема заключается в попытке систематизировать имеющиеся знания по теме. Причиной выбора этого метода является то, что он повышает интерес к занятиям, облегчает восприятие, снимает нервное напряжение и повышает эффективность урока. Все этапы урока соблюдены. Это следующие этапы - вызов, осмысление, рефлексия и домашнее задание и, благодаря форме урока, имеют плавный переход от одного к другому.

В начале урока я, проверяю домашнее задание в игровой форме: «Вычеркнуть ненужный символ», «Разгадать кроссворд», «Блиц опрос», тем самым провожу актуализацию знаний, стараясь вызвать интерес к познанию. Урок сопровождается атмосферой сотрудничества. Я думаю, что такой подход имеет важное воспитательное значение.

1.Этап «Вызов» введение в проблему, актуализация имеющегося опыта и знаний учащихся необходима для определения темы урока самими учащимися. Я использую прием «Составление кластера».

2. Этап «Осмысление». Этот этап можно по-другому назвать смысловой стадией. На большинстве уроков в школе, где изучается новый материал, эта фаза занимает наибольшее время. Одним из условий развития критического мышления является отслеживание своего понимания при работе с изучаемым материалом. Именно данная задача является основной в процессе обучения на фазе осмысления содержания. Поэтому, после вывода , я включаю, устные задания на применение формул. Важным моментом является получение новой информации по теме. Чтобы поддерживать активность учащихся, их интерес и инерцию движения, созданную во время фазы вызова, я включаю в урок рассказы «Из истории математики». В любом случае это будет индивидуальное принятие и отслеживание информации. В этом смысле важное значение имеет качество отобранного материала. По ходу объяснения рассказа с применением интересных фактов и комментариев («Легенда о царевне Дидоне»), я ставлю проблемные вопросы, так необходимые, в режиме технологии развития критического мышления, тем самым стимулирую учащихся к постановне новых вопросов, поиск ответов через контекст той информации, с которой учащиеся работают. На смысловой стадии учащиеся самостоятельно продолжают активно конструировать цели своего учения. Постановка целей в процессе знакомства с новой информацией осуществляется при ее наложении на уже имеющиеся знания. Школьники могут найти ответы на ранее заданные вопросы, решить возникшие на начальном этапе работы затруднения.

3. Этап «Рефлексия». На этом этапе

Рефлексивный анализ проблем, осваиваемый учащимися, является необходимым условием выработки у них приемов самостоятельной постановки задач, гипотез и планов решений, критериев оценки полученных результатов.

Тем самым развивается способность учащихся саморегуляции учебной деятельности и к самообразованию в целом.

В соответствии с рациональной организацией урока, заключительной его частью являлась рефлексия, то есть самооценка. Цель этого этапа – определить, насколько хорошо и точно усвоена эта часть учебного материала, и можно ли двигаться дальше, организовывать усвоение учащимися новой части учебного материала.

4. Этап «Домашнее задание»

Домашнее задание разноуровневое, творческое, дает учащимся право выбора. Первый вариант предполагает решение заданий, второй – носит творческий характер, составить синквейн на тему «Окружность. Круг». Почему именно такое домашнее задание для учащихся было выбрано. Ежедневно учащиеся при подготовке к уроку выполняют различные вычисления, решают примеры, задачи и иногда для формирования положительного мотива учения учащимся предлагается домашнее задание разноуровневое с правом выбора задания.

На изучение технологии критического мышления и апробации методики критического мышления , у меня на каждом уроке, отводилось немного времени, в течении которого на уроках математики учащиеся учились составлять кластер , писать синквейны и эти приемы наиболее успешны в практическом применении.

Сочетание различных форм работы (индивидуальная, фронтальная, групповая) позволило вовлечь учащихся в активный процесс общения. Фронтальная работа предусматривала совместную деятельность учителя и учеников. Для стимулирования мыслительной деятельности учащихся я использовала объяснительно-иллюстративный метод, частично-поисковый метод, исследовательский.

Зрительному восприятию способствовала подобранная наглядность.

На уроке использовала принцип от простого к сложному, принцип доступности.

Используя здоровьесберегающие технологии, я провела физминутку. Физминутка - урока была связана с эмоциональной составляющей урока и плавно подводила учащихся к продолжению изучения нового материала урока. Произошла смена деятельности в предметном смысле.

Умение применять знания в практических ситуациях прослеживалось в решении задач. Дети использовали ранее полученные знания по теме «Окружность и круг». Домашнее задание разноуровневое, творческое, дает учащимся право выбора.

Я считаю, что цель урока достигнута. Выводы, сделанные учащимися, отражают их понимание темы.

Синквейн на тему Окружность

Окружность
числовую, единичную
чертят, соединяют, обозначают
кривую, все точки которой равноудалены от центра
фигура