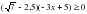Конспект урока по теме «Решение линейных неравенств»- 8 класс
Цели: Систематизировать знания по теме «Линейные неравенства» (подготовка к контрольной работе)
Тип урока :повторительно-обобщающий
1) Образовательные: Воспитательные: воспитывать интерес к чтению, бережное отношение к книге, понимание роли художественной литературы в формировании личности человека.
2) Развивающие: развитие навыков анализа, обобщения, систематизации; развитие речи учащихся.
3) Воспитательные: воспитывать стремление к повышению уровня знаний, умение работать в парах, внимание, самооценку и взаимооценку, умение работать с тестовыми заданиями.
СЛАЙД 0 Приветствие обучающихся, объявление темы урока, постановка целей и задач урока.
Тема урока: « Решение линейных неравенств»
Блиц опрос: (Дети работают в тетрадях, записывают ответы в таблицу).
Таблица дана в приложении 1.
- СЛАЙД 1
Найдите значение выражения -2х+3 при х равном а) ½; б)1,5; в)1; г)-1?
- СЛАЙД 2
Решением какого неравенства является число -2?
А) -2х<3 Б)-2х+3≤0 В ) 2х-3<0
Ответ: В
- СЛАЙД 3 Определите знак числа
Дети используют таблицу квадратов.1)корень из 5 минус2 2 )1минус корень из 3 в)2,8 минус корень из 8
- СЛАЙД 4
Из данных неравенств выберите номера тех неравенств, которые верны при всех значениях переменной. Ответ запишите в виде числа.
1) а2+4>0 2) (а-4)2>0 3) -(а+6)2>0 4)а2+(-а)2>0
Ответ: 124
- СЛАЙД 5
Подведём итог: Дети подсчитывают баллы за блиц опрос (Каждое задание оценивается в 1 балл) Взаимопроверка в парах.
- В следующих заданиях определите, верно ли выполнено преобразование неравенств. Если нет, найдите ошибку.
Выполняя это задание, дети повторяют теоремы о свойствах неравенств. Слайд 6 , Слайд 7
Слайд 8 Слай9
- Сопоставьте графические модели неравенств с аналитической моделью.
Слайд 10 , Слайд 11, Слайд 12
1.Для более подготовленных учащихся предлагаются задания повышенного уровня сложности по группам в соответствии с уровнем подготовленности группы из 2 части ОГЭ 9 класса.
2.Дополнительное задание для учащихся среднего уровня подготовки (1 группа)
При каких значениях переменной х выражение корень квадратный из 5х-2 имеет смысл?
3.Дополнительное задание для учащихся более высокого уровня подготовки (2 группа)
При каких значениях параметра а уравнение 2а-3х=3а+1 имеет положительный корень?
- Задания повышенного уровня проверяются и оцениваются учителем индивидуально по мере выполнения их учащимися.
Самостоятельная работа (по вариантам) СЛАЙД 14
Решит неравенство
1 вариант 2 вариант
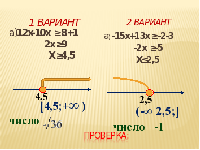
а)12х-1>8+10х б)3(х+4)>2(х+5)-(3-х) а)-15х+3>-2-13х б)2(х-3)<3(х-1)-(х+5)
СЛАЙД 15 Слайд 16
Слайд 17 Проверка (Дети самостоятельно осуществляют проверку и ставят себе баллы в таблицу оценок)
Работа по группам.
1 группа (Учащиеся слабого и среднего уровня)
При каких х дробь (16-3х)/3 < (3х+7)/4 Совместное решение у доски.
2 группа (учащиеся более высокого уровня подготовки)
Слайд 18 , Слайд 19
Слайд 20
Решение задачи на применение неравенств.
При изготовлении бланков фирма берёт по 60 рублей за бланк и ещё 115 руб. за заказ. Магазин продаёт бланки по 80 рублей за бланк.
Какое наименьшее число бланков можно купить,чтобы выгоднее было сделать заказ в фирме,чем купить в магазине?
Подведение итогов урока. Выставление баллов в таблице
(Смотри приложение 1)
Выставление оценок.
Постановка домашнего задания : индивидуальные тесты
(Смотри приложение 2)
Приложение 1
Заполни ответы в таблицу
задание
Заполни клетки таблицы
Оценка в баллах
Оценка
6-7 баллов –«3» 8-9 баллов –«4» 10 и более баллов -«5»
Приложение 2
Домашняя работа по теме: «Решение линейных неравенств»
1 вариант
- Решите неравенство 2х-3>0
1)(-∞;1,5) 2)(-∞;-1,5) 3)(1,5;+∞) 4)[1,5;+)
2.Найдите наибольшее целое число, которое является решением неравенства
-2х + 8 ≥ 3х – 2
1)6 2)-6 3)2 4)-2
3. Найдите Количество целых решений неравенства -3х<1,2, принадлежащих промежутку [-2;2]
1)-5 2)2 3)4 4)3
4.При каких значениях х дробь принимает значения меше 0?
1)х≤2,5 2)х>2,5 3 )х >2,5 4 ) х<-2,5
5.При каких х значение выражения 3(х-4) не меньше значения выражения х+5?
1)х≥9,5 2)х<8,5 3)х≥-8,5 4)х≥8,5
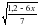
6.Найдите множество решений неравенства
7. При каких значения переменной выражение имеет смысл?
8. Решите неравенство
9* При каких значениях параметра В уравнение 3-В=5+х имеет положительный корень
2 вариант
- Решите неравенство 2х-1<0
1)(-∞;0,5) 2)(-∞;-0,5) 3)0,5;+∞) 4)[0,5;+)
2.Найдите наибольшее целое число, которое является решением неравенства
-3х + 6 ≤ 3х – 6
1)6 2)-6 3)2 4)-2
3. Найдите Количество целых решений неравенства -4х<1,2, принадлежащих промежутку [-1;1]
1)-3 2)2 3)4 4)3
4.При каких значениях х дробь (2х-5)/3 принимает значения больше 0?
1)х≤0,5 2)х>2 3 )х >0,5 4 )х<-2
5.При каких х значение выражения 5(х-4) не больше значения выражения х-2?
1)х≥5,4 2)х≤4,5 3)х≥-4,5 4)х≤5,4
6.Найдите множество решений неравенства 3х/5-(х-2)/4+(х+1)/2<2
7. При каких значения переменной выражение корень квадратный из (2-6х)/7 не имеет смысла?
8. Решите неравенство
9* При каких значениях параметра В уравнение 7-В=2+х имеет положительный корень
 Варианты ответов
Варианты ответов Решением какого неравенства является число -2?
Решением какого неравенства является число -2?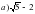 б)1-
б)1-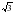 в)2,8-
в)2,8-
 Ответ:
Ответ: 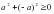
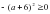
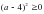
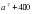 1) 2) 3) 4)
1) 2) 3) 4)
 Подведём итог: Дети подсчитывают баллы за блиц опрос (Каждое задание оценивается в 1 балл) Взаимопроверка в парах.
Подведём итог: Дети подсчитывают баллы за блиц опрос (Каждое задание оценивается в 1 балл) Взаимопроверка в парах. 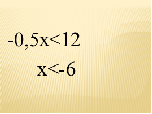
 Слайд 6 Слайд 7
Слайд 6 Слайд 7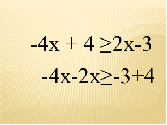

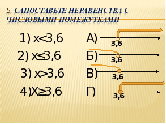 Слайд 11
Слайд 11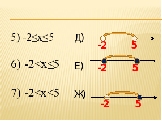

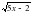 имеет смысл?
имеет смысл?
 Слайд 16
Слайд 16 Слайд 17 Проверка
Слайд 17 Проверка  Совместное решение у доски.
Совместное решение у доски. 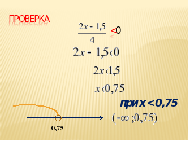


 Постановка домашнего задания
Постановка домашнего задания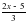 дробь принимает значения меше 0?
дробь принимает значения меше 0?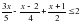
 имеет смысл?
имеет смысл?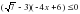
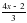 дробь принимает значения больше 0?
дробь принимает значения больше 0?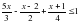
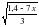 не имеет смысла?
не имеет смысла?