Конспект урока математики, презентация для урока алгебры "Что такое функция?"

Учитель математики: Шарипова Зинура Кадыровна

2015 – 2016 учебный год

Место урока: 7 класс. Алгебра. Первый урок главы “Функции”.

Роль урока:

Первые шаги в формировании фундаментального понятия школьного курса алгебры – понятия “функция”.

Цели урока:

• формирование представлений о функции как математической модели, описывающей реальные процессы

• формирование первоначальных представлений о функции как зависимости одной переменной от другой

• формирование и первичная отработка понятий “функция”, “аргумент функции”, “значение функции”, “независимая переменная”, “зависимая переменная”

• формирование представлений о способах задания функций

• отработка умений решения простейших задач, опираясь на графики и таблицы

• развитие грамотной математической речи

Оборудование и дидактические материалы:

1. Компьютер

2. Мультимедиа-проектор

3. Экран ПК

4. Презентация для показа на компьютере (Приложение1).

Ход урока:

I. Организационный момент.

Тема урока. Цели урока. Слайд1. Слайд 2.

II. Актуализация темы.

Краткая беседа о том, что в окружающем мире абсолютно всё находится в какой-либо зависимости от чего-либо. Примеры. (С опорой на учащихся, дать волю их фантазии, причём возможны самые нелепые примеры с точки зрения математики: например, настроение зависит от погоды). Математика нашла способы описания зависимостей. Слайд 3.

III. Изучение нового материала.

Сообщается, что главным, ключевым словом на уроке является слово “зависимость”. Слайд 4.

1. Работа с учебником. Комментированное чтение п. 10, 1, 2, 3, 4, 5 абзац. Запись в тетрадях примера зависимости площади квадрата от длины его стороны. Слайд 5.

2. Обсуждение ситуации. Ответы на вопросы: значение какой переменной является зависимой, а какой – независимой; какие значения переменной а можно задавать; как найти значение переменной s. Вывод: изменение одной величины в рассмотренном примере приводит к изменению другой.

3. Беседа с учащимися. Приводятся и обсуждаются примеры зависимостей одной величины от другой, более связанные с конкретными науками – математикой, физикой и др. Слайд 6.

4. Сообщается, что в математике, в частности, в алгебре, придумано формальное описание различных зависимостей с помощью формул, причём принято независимую переменную обозначать буквой х, а зависимую – буквой у. Вот что при этом получается. Слайд 7.

5. Запись учащихся в тетрадях. Новые термины. Слайд 8.

6. Закрепление новых терминов, применяя их к ранее рассмотренным примерам зависимостей. Например, назвать величину, играющую роль аргумента или назвать зависимую переменную в какой-либо конкретной зависимости.

7. Работа с табличным способом задания функции. Рассмотрим зависимость, заданную несколько иначе - с помощью таблицы. Слайд 9 . Обсуждение примера. Ответы учащихся на вопросы: какая переменная является независимой, зависимой? Какую переменную следует называть аргументом функции, а какая является значением функции? Какие значения могут принимать значения переменных?

8. Работа с графическим способом задания функции. Рассмотрим зависимость, заданную с помощью графика. Какая величина независимая, зависимая? Какую переменную следует называть аргументом, какую – значением функции? Возможные значения переменных. Слайд 10.

9. Отработка умений работать с графиком: найти значения функции, соответствующие значению аргумента, равному 2, 6, 9, 14, 22, 24; найти самое большое значение функции и соответствующее значение аргумента; в какое время температура была отрицательна; при каких значениях аргумента значения функции принимали положительные значения и др.

10. Знакомство с понятием функции. Во всех примерах рассматривались зависимости одной величины от другой. Определение. Запись определения в тетрадях (в учебнике нет чёткого определения).

Слайд 11.

1. Факты из истории. Слайд 12.

2. Обсуждение с учащимися возможных способов задания функций на основе рассмотренных на уроке примеров. Запись в тетради. Слайд 13.

IV. Закрепление новых понятий

• Задание №1. Совместное обсуждение. Слайд 14.

• Задание №2. Совместное обсуждение. Слайд 15.

V. Домашнее задание. Подробный комментарий. Дополнительное задание. Слайд 16.

Проверка степени понимания и глубины усвоения рассмотренного на уроке материала. Ответы на вопросы на листочках. Слайд 17. Слайд 18.

Сбор листочков на проверку. Отметки выставлять по усмотрению учителя: хорошие отметки выставить всем учащимся, плохие – по согласованию с учащимися.

Обсуждение правильности ответов задания слайда № 18.

VI. Итоги урока. Что должны были усвоить и как усвоили. Что нового открыли для себя на уроке.

Что такое функция?

7 класс

Первый урок по теме «Функции»

Цели урока:

• Ознакомиться с понятием « функция », закрепить его на примерах
• Усвоить новые термины:

зависимая переменная и независимая переменная

( аргумент функции и значение функции ).

• Узнать способы задания функции.

Закрепить их при решении задач

Понятие функции можно считать стержнем, вокруг которого группируется преподавание математики

Никакое другое понятие не отражает

явлений реальной действительности

с такой конкретностью, как понятие

функциональной зависимости

Ключевое слово урока:

зависимость

Первый пример зависимости одной величины от другой (с помощью формулы)

Площадь квадрата зависит от длины его стороны. Если изменить длину стороны квадрата, то изменится и значение площади.

S = a * a

Если а=3, то S =3*3=9(ед кв)

Если а=0,4, то S =0,4*0,4 = 0,16(ед кв)

3

0,4

Другие примеры зависимостей

• Периметр квадрата зависит от длины его стороны: Р = 4 а ( р зависит от а )
• Пройденный путь зависит от времени движения: S = t v ( s зависит от t )
• Пройденный путь зависит от скорости:

S = v t ( s зависит от v )

• Ваши примеры

Описание зависимостей с помощью формул

• У = 4 х

• У = t х

• У = v х

• Р = 4 а ( р зависит от а )

• S = t v ( s зависит от t )

• S = v t ( s зависит от v )

• а (длина стороны)
• Аргумент функции
• Независимая переменная

• S (значение площади)
• Значение функции
• Зависимая переменная

Второй пример зависимости одной величины от другой (табличный):

В таблице показана зависимость количества выпущенных заводом электроплит от порядкового номера месяца, в котором были выпущены электроплиты

х

у

1

2

230

3

270

4

310

300

5

6

360

340

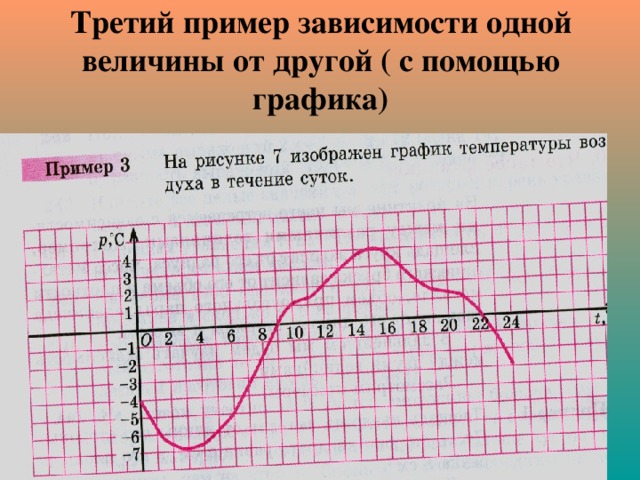
Третий пример зависимости одной величины от другой ( с помощью графика)

Что же такое функция?

Функцией называют такую зависимость

переменной у от переменной х ,

при которой

каждому значению х

соответствует

единственное значение у

Факты из истории.

• Термин «функция» - от латинского functio - совершение, выполнение
• Первоначально понятие функции как выражения сложилось в 17 веке
• В 18 веке основным объектом изучения математики стали зависимости между переменными величинами
• Впервые термин функция ввёл И.Бернулли в 1718 году
• В общем виде определение функции было дано Н.И. Лобачевским в 1934 г.

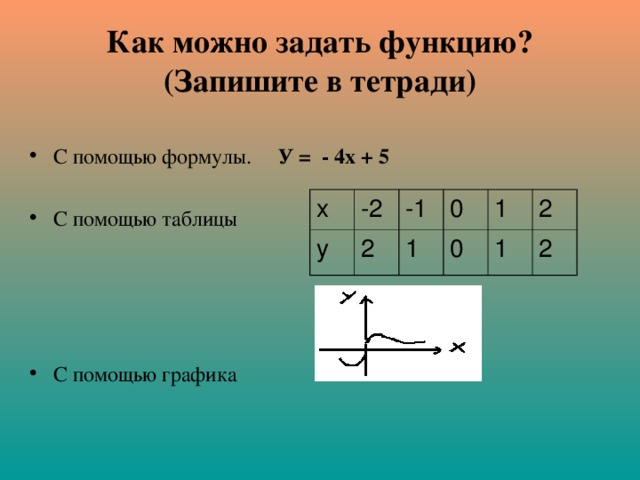
Как можно задать функцию? (Запишите в тетради)

• С помощью формулы. У = - 4х + 5

• С помощью таблицы

• С помощью графика

х

у

-2

2

-1

1

0

0

1

2

1

2

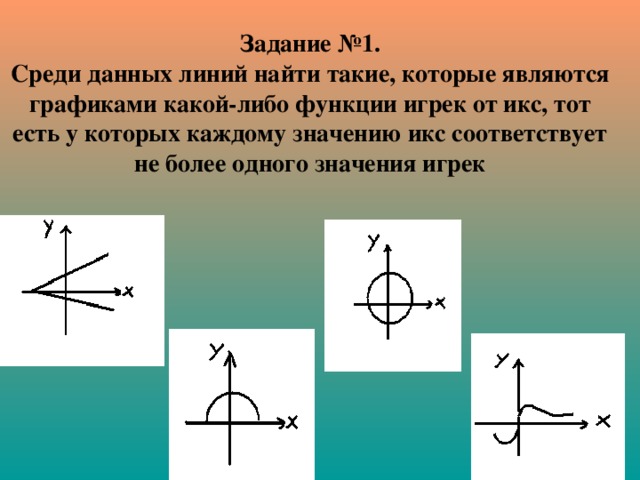
Задание №1. Среди данных линий найти такие, которые являются графиками какой-либо функции игрек от икс, тот есть у которых каждому значению икс соответствует не более одного значения игрек

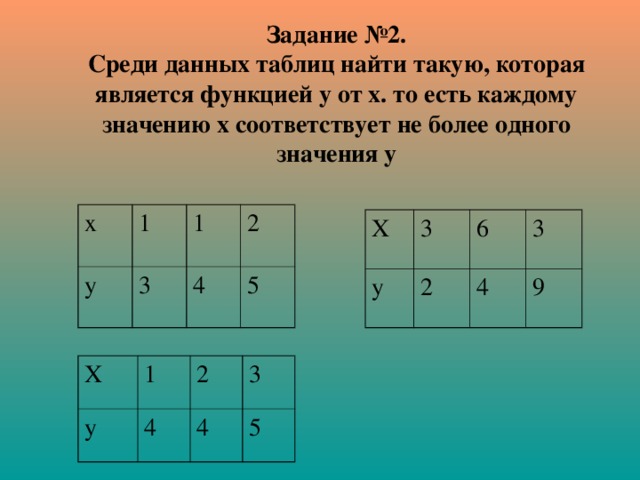
Задание №2. Среди данных таблиц найти такую, которая является функцией у от х. то есть каждому значению х соответствует не более одного значения у

х

1

у

1

3

2

4

5

Х

3

у

6

2

3

4

9

Х

1

у

2

4

3

4

5

Домашнее задание (записать в дневники)

• Читать П 10, стр 39 – 41 ( до последнего определения), выучить определение функции и значения новых терминов
• № 252, № 255,№ 188(а)
• Желающие находят дополнительный материал по теме «История появления понятия «функция»

Дайте ответы на вопросы .

• Как вы поняли, что такое функция?
• Приведите два примера зависимости одной величины от другой
• Какими способами может быть задана функция?
• Как иначе можно назвать независимую переменную ?
• Как иначе можно назвать зависимую переменную?
• Выполни задание на слайде №18.

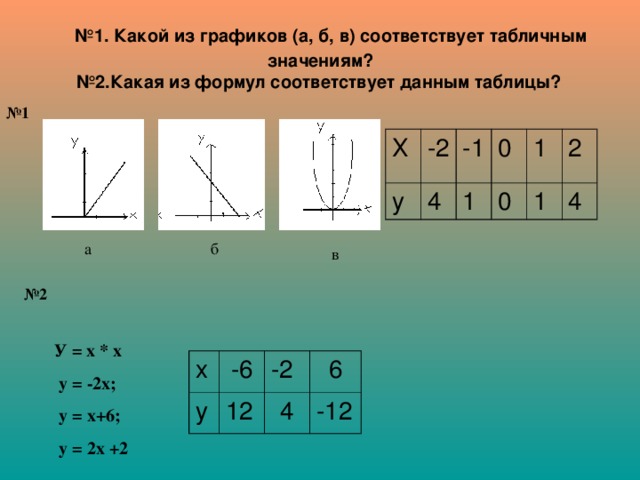
№ 1. Какой из графиков (а, б, в) соответствует табличным значениям? №2.Какая из формул соответствует данным таблицы?

№ 1

Х

у

-2

4

-1

1

0

0

1

1

2

4

а

б

в

№ 2

У = х * x

у = -2х;

у = х+6;

у = 2х +2

х

у

-6

-2

12

6

4

-12