КОНСПЕКТ УРОКА МАТЕМАТИКИ В 7 КЛАССЕ ПО ТЕМЕ
«Взаимное расположение графиков линейных функций»
учебник Ш.А.Алимов и др. Алгебра. 7 класс. М.: Просвещение, 2000.
Цель урока: создать условия для получения учащимися новых знаний через проведение исследования, обработку полученных результатов и умение делать выводы.
Задачи:
- предметные: обосновывать, что графиком линейной функции является прямая;
рассмотреть случаи взаимного расположения прямых – графиков линейных функций;
развивать навыки построения прямых по координатам точек; способствовать представлению о взаимном расположении графиков линейных функций, построения их на основе традиционных и инновационных ресурсов.
-метопредметные
Регулятивные: работают по составленному плану, используют наряду с основными и дополнительные средства построения графиков линейных функций. В диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки.
Познавательные: использовать поиск необходимой информации для выполнения учебных заданий с использованием ЭОР.
Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.
- личностные: проявлять положительное отношение к урокам алгебры, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; дают позитивную оценку и самооценку учебной деятельности; анализируют соответствие результатов требованиям конкретной учебной задачи.
Тип урока урок – изучения нового материала Вид урока Урок – исследование
ХОД УРОКА
I. Организационный момент. Приветствие
II.Актуализация. На прошлом уроке мы с вами познакомились с понятием линейная функция. При изучении нового материала мы всегда опираемся на ранее изученный материал.
Фронтальный опрос + устная работа с целью повторения ранее изученного материала
В ходе подготовки к устной работе приготовьтесь ответить на следующие вопросы:
1) Какая функция называется линейной?
2) Что является графиком линейной функции?
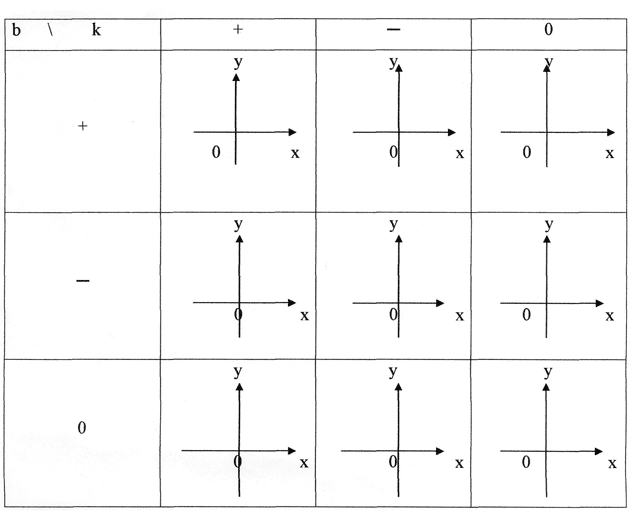
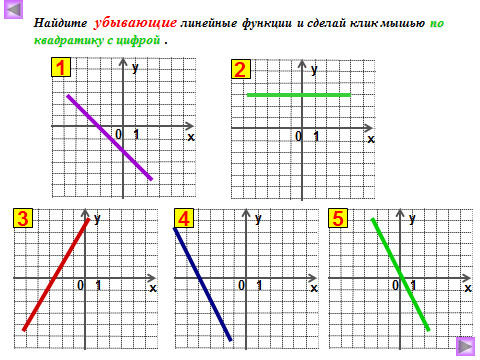
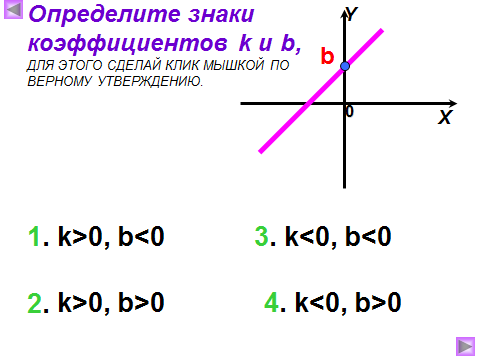
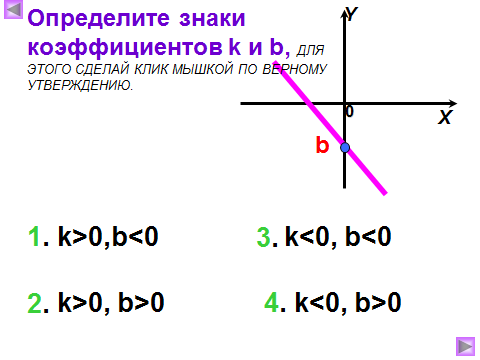
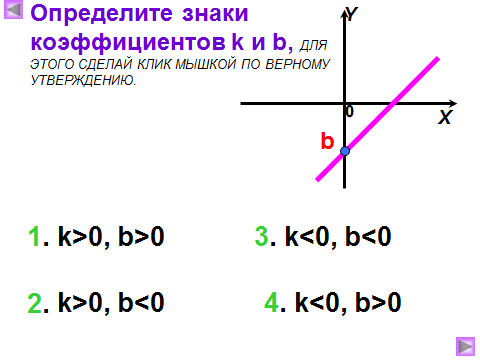
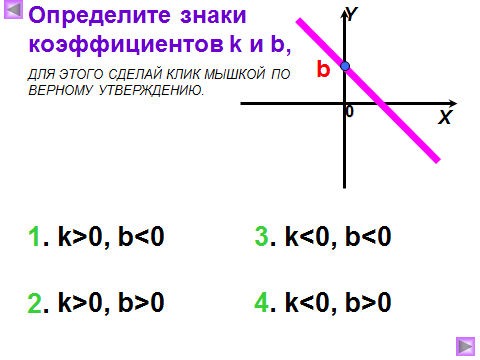
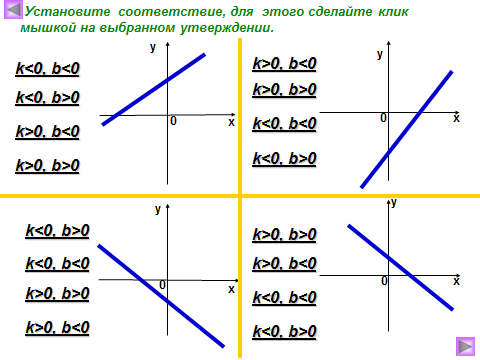
3) Как называют число k? Что оно показывает? Как влияет знак коэффициента k на положение графика в системе координат?
4) Как называется число b? Что показывает число b?
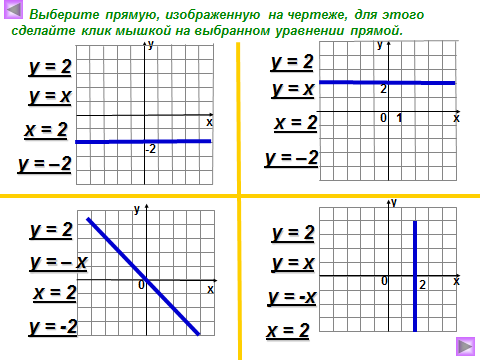
5) Что представляет собой график линейной функции, если угловой коэффициент равен 0?
Работа в парах (см приложение 2)
Отчет каждой группы. Подведение итогов работы групп, исправление ошибок, если они будут.
Проверим, насколько вы были внимательны во время устной работы.
Физ. минутка. (работа со слайдами 13,14,15,16 см презентацию)
Учитель просит детей сильно зажмурить глаза, после чего открывает слайд 13 и просит открыть глаза и найти ошибку. Дети находят ошибку, учитель показывает правильный ответ. Опять просит зажмурить глаза, включает следующий слайд и т.д.
III.Изложение нового материала
1. Цель: Обеспечить целеполагание.
- Мы с вами знаем, что графиком линейной функции является прямая. Каково взаимное расположение прямых на плоскости? /параллельны, пересекаются, совпадают/
- Можно ли наш вывод о взаимном расположении прямых на плоскости применить к графикам линейных функций? На основе предыдущих рассуждений попытайтесь самостоятельно сформулировать тему урока.
(«Взаимное расположение графиков линейных функций»)
- Сформулируйте своими словами цель работы на уроке, что нового должны узнать на уроке, что выяснить, чему научиться?
/ Каково взаимное расположение графиков линейных функций,
от чего зависит взаимное расположение графиков линейных функций. Можно ли без построения графиков определить взаимное расположение графиков линейных функций./
Учитель корректирует ответы учащихся.
2. Лабораторная работа
по теме «Взаимное расположение графиков линейных функций»
Исследование взаимного расположения графиков линейных функций от значений k и b.
Цель работы: выяснить, как зависит взаимное расположение графиков линейных функций от значений k и b.
Группа №1.
Выяснить взаимное расположение графиков функций у = х – 2 и у = х + 1.
Инструкция
1) В одной системе координат постройте графики у = х – 2 и у = х + 1.
2) Запишите, а затем сравните угловые коэффициенты k1 = ____; k2 = ____; k1 k2 (равны или не равны)
3) Запишите, а затем сравните свободные члены b1___; b2 = _____; b1 b2 (равны или не равны)
4) Сделайте вывод о взаимном расположении графиков функций.
Вывод: Из рисунка видно, что прямые, заданные этими функциями ________________
Запишите вывод с помощью математических символов:
Если ______________ , __________________, то эти прямые ____________________.
Вывод:
Из рисунка видно, что прямые, заданные этими функциями параллельны.
Таким образом, если угловые коэффициенты k прямых y = kx + b одинаковы, а значения b различны, то эти прямые параллельны.
Группа № 2.
Выяснить взаимное расположение графиков функций у = – х + 2 и у = 2х + 1.
Инструкция
1) В одной системе координат постройте графики у = – х + 2 и у = 2х + 1.
2) Запишите, а затем сравните угловые коэффициенты k1 = ____; k2 = ____; k1 k2 (равны или не равны)
3) Запишите, а затем сравните свободные члены b1 = ____; b2 = _____; b1 b2 (равны или не равны)
4) Сделайте вывод о взаимном расположении графиков функций.
Вывод: Из рисунка видно, что прямые, заданные этими функциями _________
Запишите вывод с помощью математических символов:
Если ______________ , __________________, то эти прямые ____________________.
Группа № 3.
Выяснить взаимное расположение графиков функций у = 2х – 1 и у = 4/2х - 3/3.
Инструкция
1) В одной системе координат постройте графики у = 2х – 1 и у = 4/2х - 3/3.
2) Запишите, а затем сравните угловые коэффициенты k1 = ____; k2 = ____; k1 k2 (равны или не равны)
3) Запишите, а затем сравните свободные члены b1 = ____; b2 = _____; b1 b2 (равны или не равны)
4) Сделайте вывод о взаимном расположении графиков функций.
Вывод: Из рисунка видно, что видно, что графики двух данных функций _______________
Запишите вывод с помощью математических символов:
Если ______________ , __________________, то эти прямые ____________________.
Вывод: видно, что графики двух данных функций совпадают.
Вывод:
Пусть функции заданы формулами y = k1 x + b1 и y = k2 x + b2
1. Если k1 ≠ k2 , b1 ≠ b2, то эти прямые пересекаются.
2. Если k1 = k2 , b1 ≠ b2, то эти прямые параллельны.
3. Если k1 = k2 , b1 = b2, то эти прямые совпадают.
Отчет каждой группы. Подведение итогов работы групп, исправление ошибок, если они будут. Заполнение памятки.
IV.Формирование умений и навыков
Этап первичного закрепления новых знаний.
Задание № 1. Функции заданы формулами
1) у = -1,5х + 6 2) у = 0,5х + 6 3) у = 0,5х + 4 4)у = 0,5х 5)у = 3 + 1,5х
Выпишите те, из них которые:
1) Параллельны графику функции у = 0,5х + 10 ( 2,3 и 4)
2) Пересекают график функции у = -1,5х (2,3,4 и 5)
Задание 2.
Дана линейная функция у = 2,5х – 4. Задайте формулой какую-нибудь линейную функцию, график которой
1) параллелен графику данной функции;
2) пересекает график данной функции.
Задание 3. Найдите лишнюю функцию, ответ обоснуйте
1) у= - 2х + 0,3; у = -2х + 4; у = 3 - 2х; у = х + 1; у = - 2х; у = - 2?
2) у = х + 3; у = 2(0,5х + 1,5); у = 3 - х; у = 3 + х; у = ?
Задание 4.
1. При каких значениях параметров графики данных функций пересекаются?
у = 2ах +5 и у = 5х – 2. (Ответ: а ≠ 2,5)
2. При каких значениях параметров графики данных функций параллельны?
у = 3ах + 5 и у = 6х – 2. (Ответ: а = 2)
3. При каких значениях параметров графики данных функций совпадают?
у = 2ах + 7 и у = 9х + 7 (Ответ: а = 4,5)
V. Подведение итогов урока, постановка задания на дом.
– Каково взаимное расположение двух прямых на плоскости?
– Условие пересечения графиков двух линейных функций?
– При каком условии графики линейных функций параллельны?
– Условие совпадения графиков линейных функций?
VI. Домашнее задание: п. 32, № 610. Рекомендую при построении графиков разных функций применять цветные пасты. Не забывайте делать выводы, как зависит взаимное расположение графиков линейных функций от значений b и k.
VII. Рефлексия + тест (при наличии времени)
Продолжите фразу:
Сегодня на уроке я повторил…
Сегодня на уроке я узнал….
Сегодня на уроке я научился….
У меня хорошо получилось…
Я хотел бы еще…
Просмотр содержимого документа
«Взаимное расположение графиков линейных функций»
КОНСПЕКТ УРОКА МАТЕМАТИКИ В 7 КЛАССЕ ПО ТЕМЕ
«Взаимное расположение графиков линейных функций»
учебник Ш.А.Алимов и др. Алгебра. 7 класс. М.: Просвещение, 2000.
Урок подготовила и провела Кузнецова С.Д.,
учитель математики МКОУ ООШ № 4, г. Красноуфимск
Цель урока: создать условия для получения учащимися новых знаний через проведение исследования, обработку полученных результатов и умение делать выводы.
Задачи:
- предметные: обосновывать, что графиком линейной функции является прямая;
рассмотреть случаи взаимного расположения прямых – графиков линейных функций;
развивать навыки построения прямых по координатам точек; способствовать представлению о взаимном расположении графиков линейных функций, построения их на основе традиционных и инновационных ресурсов.
-метопредметные
Регулятивные: работают по составленному плану, используют наряду с основными и дополнительные средства построения графиков линейных функций. В диалоге с учителем совершенствуют критерии оценки и пользуются ими в ходе оценки и самооценки.
Познавательные: использовать поиск необходимой информации для выполнения учебных заданий с использованием ЭОР.
Коммуникативные: договариваться и приходить к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.
- личностные: проявлять положительное отношение к урокам алгебры, широкий интерес к новому учебному материалу, способам решения новых учебных задач, доброжелательное отношение к сверстникам; дают позитивную оценку и самооценку учебной деятельности; анализируют соответствие результатов требованиям конкретной учебной задачи.
Тип урока урок – изучения нового материала Вид урока Урок – исследование
ХОД УРОКА
I. Организационный момент. Приветствие (1 – 2 мин)
II.Актуализация. На прошлом уроке мы с вами познакомились с понятием линейная функция. При изучении нового материала мы всегда опираемся на ранее изученный материал.
Фронтальный опрос + устная работа с целью повторения ранее изученного материала
В ходе подготовки к устной работе приготовьтесь ответить на следующие вопросы:
1) Какая функция называется линейной?
2) Что является графиком линейной функции?
3) Как называют число k? Что оно показывает? Как влияет знак коэффициента k на положение графика в системе координат?
4) Как называется число b? Что показывает число b?
5) Что представляет собой график линейной функции, если угловой коэффициент равен 0?
Работа в парах (2 – 3 мин.)
| 1 пара | 
Ответить на вопросы: 1) Какая функция называется линейной? 2) Что является графиком линейной функции? | 2 пара | 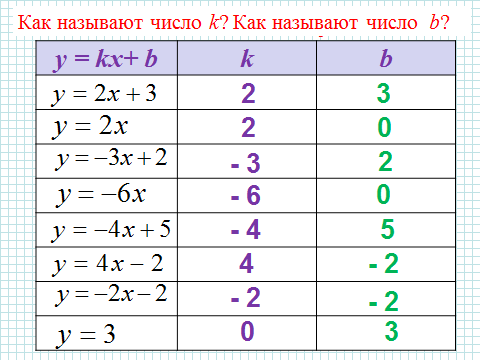
Ответить на вопросы: Как называют число k? Как называется число b? |
| 3 пара | 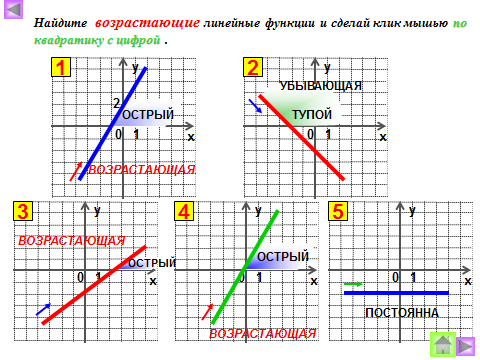 Ответить на вопросы: Ответить на вопросы:
Что показывает число k? Как влияет знак коэффициента k на положение графика в системе координат? | 4 пара | 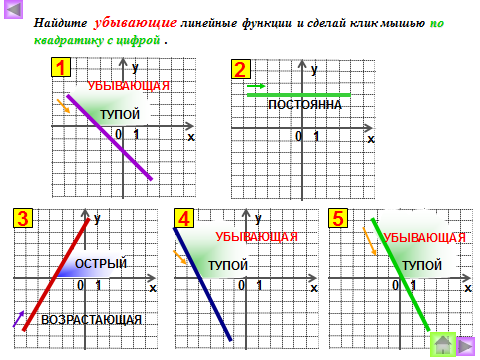 Ответить на вопросы: Ответить на вопросы:
Что показывает число k? Как влияет знак коэффициента k на положение графика в системе координат? |
| 5 пара | 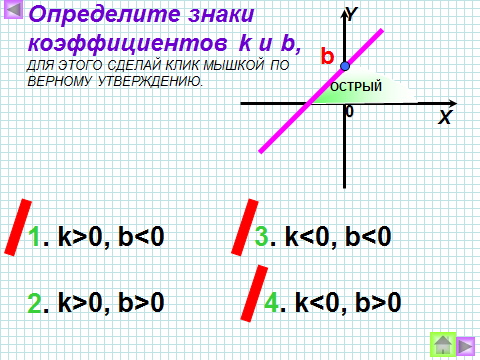 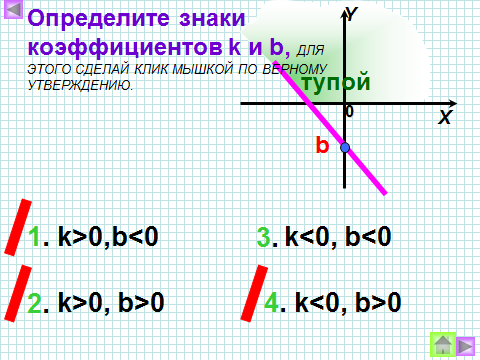 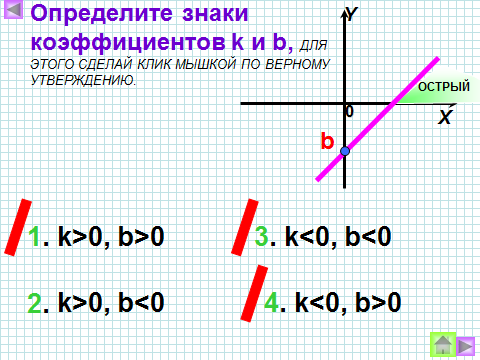 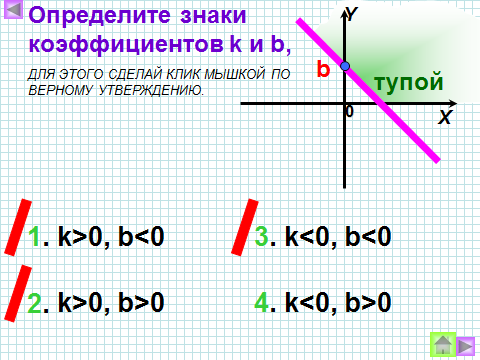
Ответить на вопрос: Как называется число b? Что показывает число b? |
| 6 пара | 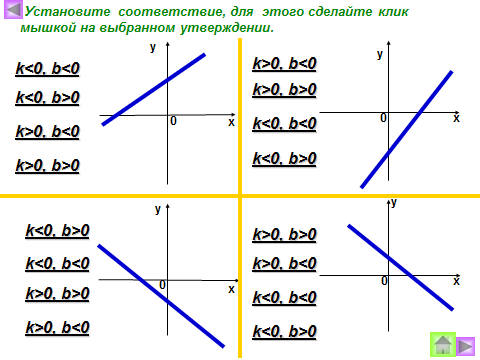
| 7 пара Что представляет собой график линейной функции, если угловой коэффициент равен 0? | 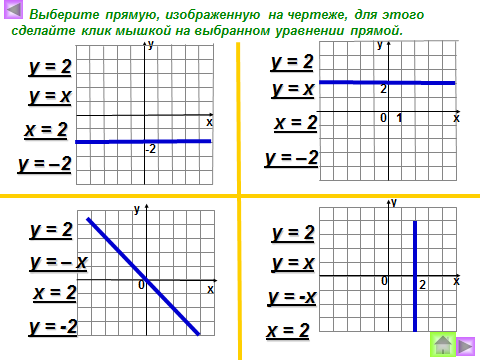
|
Отчет каждой группы. Подведение итогов работы групп, исправление ошибок, если они будут.
Проверим, насколько вы были внимательны во время устной работы.
Физ. минутка. (работа со слайдами 13,14,15,16)
Учитель просит детей сильно зажмурить глаза, после чего открывает слайд 13 и просит открыть глаза и найти ошибку. Дети находят ошибку, учитель показывает правильный ответ. Опять просит зажмурить глаза, включает следующий слайд и т.д.
Изложение нового материала
1. Цель: Обеспечить целеполагание.
- Мы с вами знаем, что графиком линейной функции является прямая. Каково взаимное расположение прямых на плоскости? /параллельны, пересекаются, совпадают/
- Можно ли применить наш вывод к графикам линейных функций? На основе предыдущих рассуждений попытайтесь самостоятельно сформулировать тему урока.
(«Взаимное расположение графиков линейных функций»)
- Сформулируйте своими словами цель работы на уроке, что нового должны узнать на уроке, что выяснить, чему научиться?
/ Каково взаимное расположение графиков линейных функций,
от чего зависит взаимное расположение графиков линейных функций. Можно ли без построения графиков определить взаимное расположение графиков линейных функций./
Учитель корректирует ответы учащихся.
2. Лабораторная работа
по теме «Взаимное расположение графиков линейных функций»
Исследование взаимного расположения графиков линейных функций от значений k и b.
Цель работы: выяснить, как зависит взаимное расположение графиков линейных функций от значений k и b.
| Группа №1. Выяснить взаимное расположение графиков функций у = х – 2 и у = х + 1. Инструкция 1) В одной системе координат постройте графики у = х – 2 и у = х + 1. 2) Запишите, а затем сравните угловые коэффициенты k1 = ____; k2 = ____; k1 k2 (равны или не равны) 3) Запишите, а затем сравните свободные члены b1 = ____; b2 = _____; b1 b2 (равны или не равны) 4) Сделайте вывод о взаимном расположении графиков функций. Вывод: Из рисунка видно, что прямые, заданные этими функциями ________________ Запишите вывод с помощью математических символов: Если ______________ , __________________ , то эти прямые ____________________.
| 
|
Вывод:
Из рисунка видно, что прямые, заданные этими функциями параллельны.
Таким образом, если угловые коэффициенты k прямых y = kx + b одинаковы, а значения b различны, то эти прямые параллельны.
| Группа № 2. Выяснить взаимное расположение графиков функций у = – х + 2 и у = 2х + 1. Инструкция 1) В одной системе координат постройте графики у = – х + 2 и у = 2х + 1. 2) Запишите, а затем сравните угловые коэффициенты k1 = ____; k2 = ____; k1 k2 (равны или не равны) 3) Запишите, а затем сравните свободные члены b1 = ____; b2 = _____; b1 b2 (равны или не равны) 4) Сделайте вывод о взаимном расположении графиков функций. Вывод: Из рисунка видно, что прямые, заданные этими функциями _________ Запишите вывод с помощью математических символов: Если ______________ , __________________ , то эти прямые ____________________.
| 1 |
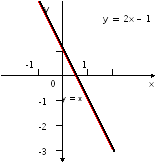
| Группа № 3. Выяснить взаимное расположение графиков функций у = 2х – 1 и у = 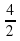 х - х - 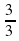 . . Инструкция 1) В одной системе координат постройте графики у = 2х – 1 и у = 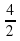 х - х - 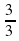 . . 2) Запишите, а затем сравните угловые коэффициенты k1 = ____; k2 = ____; k1 k2 (равны или не равны) 3) Запишите, а затем сравните свободные члены b1 = ____; b2 = _____; b1 b2 (равны или не равны) 4) Сделайте вывод о взаимном расположении графиков функций. Вывод: Из рисунка видно, что видно, что графики двух данных функций _______________ Запишите вывод с помощью математических символов: Если ______________ , __________________ , то эти прямые ____________________.
| 
|
Вывод: видно, что графики двух данных функций совпадают.
Вывод:
Пусть функции заданы формулами y = k1 x + b1 и y = k2 x + b2
1. Если k1 ≠ k2 , b1 ≠ b2 , то эти прямые пересекаются.
2. Если k1 = k2 , b1 ≠ b2 , то эти прямые параллельны.
3. Если k1 = k2 , b1 = b2 , то эти прямые совпадают.
Отчет каждой группы. Подведение итогов работы групп, исправление ошибок, если они будут. Заполнение памятки.
Формирование умений и навыков
Этап первичного закрепления новых знаний.
Задание № 1. Функции заданы формулами
1) у = -1,5х + 6 2) у = 0,5х + 6 3) у = 0,5х + 4 4)у = 0,5х 5)у = 3 + 1,5х
Выпишите те, из них которые:
1) Параллельны графику функции у = 0,5х + 10 ( 2,3 и 4)
2) Пересекают график функции у = -1,5х (2,3,4 и 5)
Задание 2.
Дана линейная функция у = 2,5х – 4. Задайте формулой какую-нибудь линейную функцию, график которой
1) параллелен графику данной функции;
2) пересекает график данной функции.
Задание 3. Найдите лишнюю функцию, ответ обоснуйте
1) у= - 2х + 0,3; у = -2х + 4; у = 3 - 2х; у = 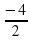 х + 1; у = - 2х; у = - 2?
х + 1; у = - 2х; у = - 2?
2) у = х + 3; у = 2(0,5х + 1,5); у = 3 - х; у = 3 + х; у = 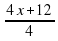 ?
?
Задание 4.
1. При каких значениях параметров графики данных функций пересекаются?
у = 2ах +5 и у = 5х – 2. (Ответ: а ≠ 2,5)
2. При каких значениях параметров графики данных функций параллельны?
у = 3ах + 5 и у = 6х – 2. (Ответ: а = 2)
3. При каких значениях параметров графики данных функций совпадают?
у = 2ах + 7 и у = 9х + 7 (Ответ: а = 4,5)
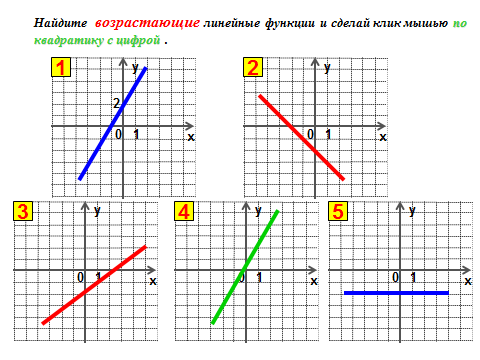
| Задание 5. 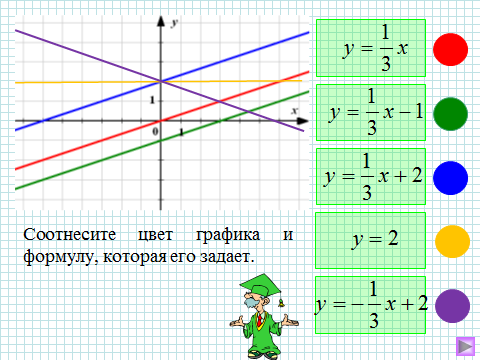
| Задание 6. Что общего в данных функциях? Каково взаимное расположение графиков функций? 
|
V. Подведение итогов урока, постановка задания на дом.
– Каково взаимное расположение двух прямых на плоскости?
– Условие пересечения графиков двух линейных функций?
– При каком условии графики линейных функций параллельны?
– Условие совпадения графиков линейных функций?
VI. Домашнее задание: п. 32, № 610. Рекомендую при построении графиков разных функций применять цветные пасты. Не забывайте делать выводы, как зависит взаимное расположение графиков линейных функций от значений b и k.
VII. Рефлексия + тест (при наличии времени)
Продолжите фразу:
Сегодня на уроке я повторил…
Сегодня на уроке я узнал….
Сегодня на уроке я научился….
У меня хорошо получилось…
Я хотел бы еще…
2
Просмотр содержимого документа
«Приложение 3. Инстукция к лабораторной работе»
Группа №1 Лабораторная работа
по теме «Взаимное расположение графиков линейных функций»
Исследование взаимного расположения графиков линейных функций от значений k и b.
Цель работы: выяснить, как зависит взаимное расположение графиков линейных функций от значений k и b.
Выяснить взаимное расположение графиков функций у = х – 2 и у = х + 1.
Инструкция
1) В одной системе координат постройте графики у = х – 2 и у = х + 1.
2) Запишите, а затем сравните угловые коэффициенты
k1 = ____; k2 = ____; k1 k2 (равны или не равны)
3) Запишите, а затем сравните свободные члены
b1 = ____; b2 = _____; b1 b2 (равны или не равны)
4) Сделайте вывод о взаимном расположении графиков функций.
Вывод: Из рисунка видно, что прямые, заданные этими функциями ________________
Запишите вывод с помощью математических символов:
Если ______________ , __________________ , то эти прямые ____________________.
Группа №1 Лабораторная работа
по теме «Взаимное расположение графиков линейных функций»
Исследование взаимного расположения графиков линейных функций от значений k и b.
Цель работы: выяснить, как зависит взаимное расположение графиков линейных функций от значений k и b.
Выяснить взаимное расположение графиков функций у = х – 2 и у = х + 1.
Инструкция
1) В одной системе координат постройте графики у = х – 2 и у = х + 1.
2) Запишите, а затем сравните угловые коэффициенты
k1 = ____; k2 = ____; k1 k2 (равны или не равны)
3) Запишите, а затем сравните свободные члены
b1 = ____; b2 = _____; b1 b2 (равны или не равны)
4) Сделайте вывод о взаимном расположении графиков функций.
Вывод: Из рисунка видно, что прямые, заданные этими функциями ________________
Запишите вывод с помощью математических символов:
Если ______________ , __________________ , то эти прямые ____________________.
Группа № 2 Лабораторная работа
по теме «Взаимное расположение графиков линейных функций»
Исследование взаимного расположения графиков линейных функций от значений k и b.
Цель работы: выяснить, как зависит взаимное расположение графиков линейных функций от значений k и b.
Выяснить взаимное расположение графиков функций у = – х + 2 и у = 2х + 1.
Инструкция
1) В одной системе координат постройте графики у = – х + 2 и у = 2х + 1.
2) Запишите, а затем сравните угловые коэффициенты
k1 = ____; k2 = ____; k1 k2 (равны или не равны)
3) Запишите, а затем сравните свободные члены
b1 = ____; b2 = _____; b1 b2 (равны или не равны)
4) Сделайте вывод о взаимном расположении графиков функций.
Вывод: Из рисунка видно, что прямые, заданные этими функциями ________________
Запишите вывод с помощью математических символов:
Если ______________ , __________________ , то эти прямые ____________________.
Группа № 2 Лабораторная работа
по теме «Взаимное расположение графиков линейных функций»
Исследование взаимного расположения графиков линейных функций от значений k и b.
Цель работы: выяснить, как зависит взаимное расположение графиков линейных функций от значений k и b.
Выяснить взаимное расположение графиков функций у = – х + 2 и у = 2х + 1.
Инструкция
1) В одной системе координат постройте графики у = – х + 2 и у = 2х + 1.
2) Запишите, а затем сравните угловые коэффициенты
k1 = ____; k2 = ____; k1 k2 (равны или не равны)
3) Запишите, а затем сравните свободные члены
b1 = ____; b2 = _____; b1 b2 (равны или не равны)
4) Сделайте вывод о взаимном расположении графиков функций.
Вывод: Из рисунка видно, что прямые, заданные этими функциями ________________
Запишите вывод с помощью математических символов:
Если ______________ , __________________ , то эти прямые ____________________.
Группа № 3 Лабораторная работа
по теме «Взаимное расположение графиков линейных функций»
Исследование взаимного расположения графиков линейных функций от значений k и b.
Цель работы: выяснить, как зависит взаимное расположение графиков линейных функций от значений k и b.
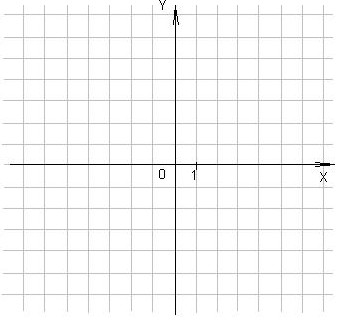
Выяснить взаимное расположение графиков функций у = 2х – 1 и у = 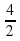 х -
х - 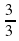 .
.
Инструкция
1)В одной системе координат постройте графики у = 2х – 1 и у = 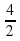 х -
х - 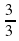 .
.
2) Запишите, а затем сравните угловые коэффициенты
k1 = ____; k2 = ____; k1 k2 (равны или не равны)
3) Запишите, а затем сравните свободные члены
b1 = ____; b2 = _____; b1 b2 (равны или не равны)
4) Сделайте вывод о взаимном расположении графиков функций.
Вывод: Из рисунка видно, что видно, что графики двух данных функций _______________________________
Запишите вывод с помощью математических символов:
Если ______________ , __________________ , то эти прямые ____________________.
Группа № 3 Лабораторная работа
по теме «Взаимное расположение графиков линейных функций»
Исследование взаимного расположения графиков линейных функций от значений k и b.
Цель работы: выяснить, как зависит взаимное расположение графиков линейных функций от значений k и b.
Выяснить взаимное расположение графиков функций у = 2х – 1 и у = 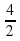 х -
х - 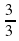 .
.
Инструкция
1)В одной системе координат постройте графики у = 2х – 1 и у = 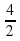 х -
х - 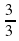 .
.
2) Запишите, а затем сравните угловые коэффициенты
k1 = ____; k2 = ____; k1 k2 (равны или не равны)
3) Запишите, а затем сравните свободные члены
b1 = ____; b2 = _____; b1 b2 (равны или не равны)
4) Сделайте вывод о взаимном расположении графиков функций.
Вывод: Из рисунка видно, что видно, что графики двух данных функций _______________________________
Запишите вывод с помощью математических символов:
Если ______________ , __________________ , то эти прямые ____________________.


 Ответить на вопросы:
Ответить на вопросы: Ответить на вопросы:
Ответить на вопросы:











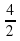 х -
х - 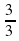 .
.
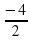 х + 1; у = - 2х; у = - 2?
х + 1; у = - 2х; у = - 2?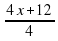 ?
? 

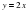
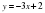
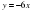
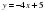
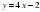
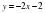
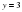
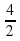 х -
х - 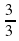 .
.
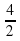 х -
х - 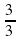 .
.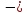 - __________, проходящая через ____________________
- __________, проходящая через ____________________















