Ф. И. О. педагога: Етеревскова _Ольга Геннадьевна_
Предмет: Геометрия__
Класс:_7_
1.Атанасян Л. С., Бутузов В. Ф. и др /Геометрия 7-9. М:Просвещение, 2004г 2. Атанасян Л. С., Бутузов В. Ф. и др./ Изучение геометрии в 7-9 кл. Книга для учителя. М: Просвещение. 2002. 3. Рабинович Е. М./ Задачи и упражнения на готовых чертежах. М: Илекса. 2000г. 4. Серия современная школа /Уроки геометрии с применением информационных технологий.М:Планета.2011г.
| Деятельность учителя | Деятельность обучающихся | Формируемые УУД |
| Регулятивные | Познавательные | Коммуникативные |
| I этап Организационный момент Слайд 1
Проверяет готовность обучающихся к работе на уроке, их рабочее место. Приветствуя учеников, создаёт ситуацию успеха.
-Здравствуйте, ребята! Давайте улыбнёмся друг другу и с хорошим настроением приступим к работе. Проверьте готовность к уроку - на столе у вас должны лежать транспортиры, линейки, ручки, карандаши, а также раздаточный материал.
|
Приветствуют учителя. Включаются в деловой ритм урока.
|
Самоконтроль; самооценка;
|
|
Планирова- ние учебного со- трудничества с учителем и свер- стниками. |
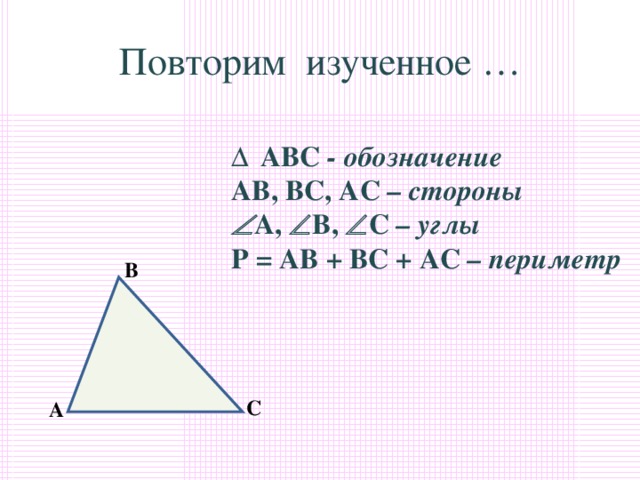
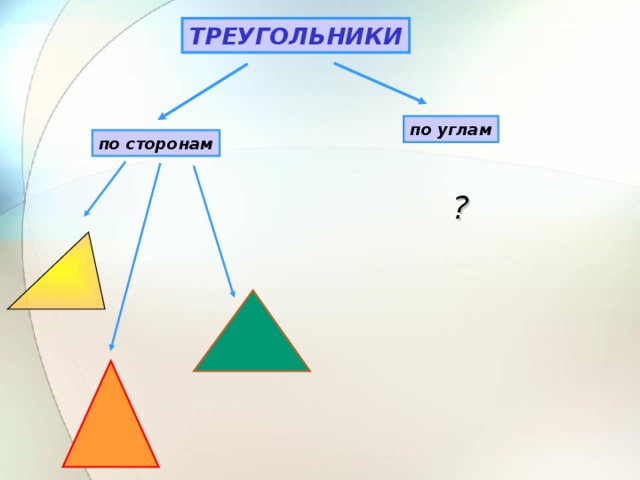
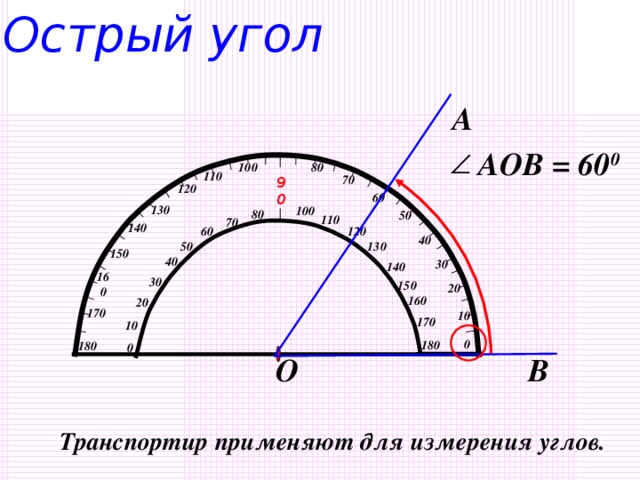
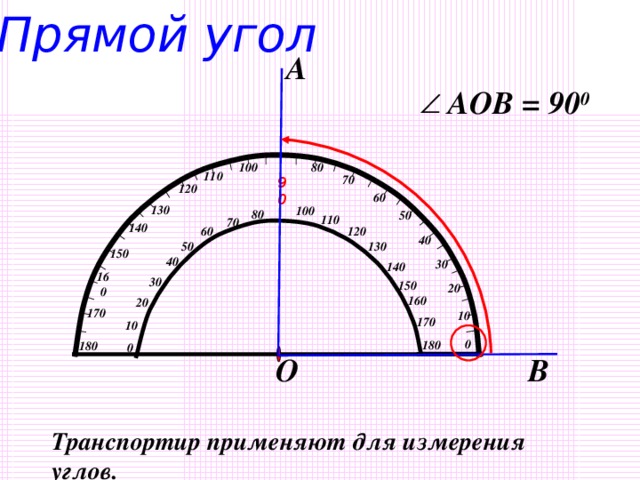
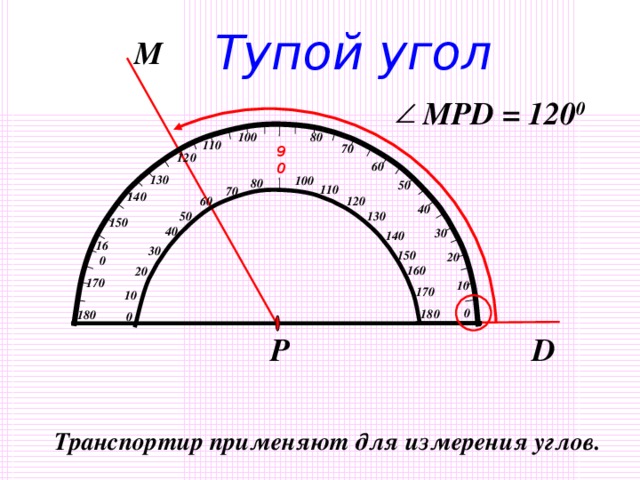
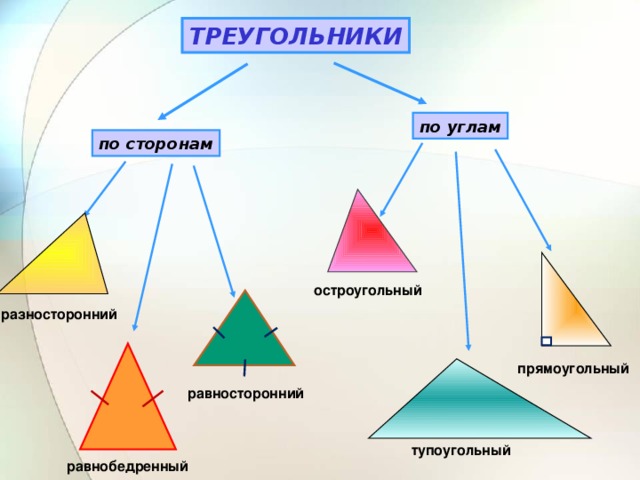
| II. Актуализация опорных знаний Слайд 2 . Задаёт вопросы, комментирует и корректирует ответы, предлагает сформулировать тему и цели урока. -Начать урок я хочу с высказывания известного итальянского физика, математика и астронома Г. Галилея:«Геометрия является самым могущественным средством для тренировки наших умственных способностей и даёт нам возможность правильно мыслить и рассуждать». Пригодится ли вам в жизни умение рассуждать, доказывать, обосновывать свою точку зрения? Итак, мы приступаем к изучению новой главы. Работаем активно, внимательно, в конце урока выполним небольшой тест по новому материалу. Показывает треугольник. -С какой фигурой работаем сегодня на уроке? Сегодняшняя тема урока связана с треугольником. Знакомый нам с детства треугольник таит в себе немало интересного и загадочного. Чтобы узнать новые свойства этой геометрической фигуры, сначала вспомним всё, что вам известно о треуголь- нике.Слайд 3 -Дайте определение треугольника? Обозначение, стороны, углы, что такое периметр? Треугольники бывают разные. Какие виды треугольников вы знаете? В зависимости от длины сторон различают равносторонние, равнобедренные и разносторонние треугольники. Слайд 4 Треугольники классифицируют не только по сторонам, но и по углам. Какими могут быть углы? От чего это зависит ? Каким прибором пользуемся для измерения углов? Возьмите в руки ручку и карандаш и покажите острый угол, прямой угол, тупой угол, развёрнутый угол. Слайд 5-7 - Какой угол называют острым? - Какой угол называют прямым? - Какой угол называют развёрнутым? - Какой угол называют тупым? Начертите в тетради три угла: острый, тупой и прямой. Дополните рисунок до треугольника. - Что для этого надо сделать? (взять по точке на сторонах угла и соединить их) - Какие получились треугольники? (тупоугольный, прямоугольный, остроугольный).Покажите на чертеже все углы треугольников. Их ещё называют внутренними углами.
|
Участвуют в работе по повторению, в беседе с учителем, отвечают на поставленные вопросы, приводят примеры
Высказывают своё мнение
С треугольником.
Устно повторяют основные понятия: треугольник, виды углов, виды треугольников по сторонам. -От градусной меры угла. Показывают углы. 1 ученик выполняет задание у доски, остальные в тетр.
| Выделение и осознание того, что уже пройдено. Постановка цели учебной задачи, синтез | Осознанное и произвольное построение речевого высказывания
| Умение с достаточной полнотой и точностью выражать свои мысли в устной форме в соответствии с задачами.
|
| III Постановка учебной задачи. Задает провокационный вопрос. -В каком треугольнике, по вашему мнению, сумма внутренних углов больше - в остроугольном, прямоугольном или тупоугольном? Как это можно проверить?. Надо измерить углы треугольников, затем найти сумму углов каждого из треугольников, сравнить результаты. Скажите, пожалуйста, кто догадался, какова будет тема урока? - Откройте тетради, запишите число, тему урока: «Сумма углов треугольника». - Как вы думаете, какова цель урока?
| Высказывают свои предположения. Отвечают на вопросы. Надо измерить углы треугольников, затем найти сумму углов треугольников, сравнить результаты. Записывают тему урока. Формулируют цель урока. | Определение и понимание учебной задачи. | Общеучебные: самостоятельное выделение – формулирование познавательной цели; логические: постановка и формулирование проблемы | Определение и формулирование цели на уроке. Высказывание предположений
|
| IV Построение проекта выхода из затруднения. Практическая работа. Задает вопросы,контролирует работу обучающихся, оказывая помощь. -Лучший способ изучить что-либо - это открыть самому. Для достижения поставленной нами цели и получения ответа на проблемный вопрос предлагаю вам выполнить задание - исследование. Работаем в парах. Раздаёт карточки с изображением треугольников. 1 ряд 2 остроугольных треугольника. 2 ряд –2 тупоугольных треугольника. 3 ряд – 2 прямоугольных треугольника. -Замерьте углы транспортиром. Найдите сумму углов. - Какие результаты получились? Сделайте вывод. А почему у вас получились неточные результаты? Создание проблемной ситуации.Случайно ли сумма углов треугольников оказалась равной 180° или этим свойством обладает любой треугольник?. Используя бумажные модели треугольников, продемонстрируйте, как можно использовать сведения о развернутом угле, при доказательстве нашего предположения. 1 практическая работа. Отрезание 2 углов модели треугольника и прикладывание к третьей вершине. Какой вывод можно сделать ? Кто-то из учащихся, возможно, предложит другой вариант. На все предложения следует обратить внимание учащихся. Давайте проверим наше предположение ещё одной практической работой. 2 практическая работа. Путем перегибания соберем углы треугольника в одну точку. Можно ли предложенные способы назвать строго научным? Однако он позволяет убедиться, что сумма углов любого треугольника 180˚. | Отвечают на вопросы учителя Выполняют практическую работу, убеждаются что получается развернутый угол.
Получают карточки. Действуют согласно указаниям Называют резуль- таты измерений. У всех результаты разные, но близкие к 180º Из-за погрешностей в измерении. Делают вывод- образуется развернутый угол. -Способ нельзя назвать строго научным. | Планирование, Прогнозирова -ние | Общеучебные: моделирование, создание способов решения проблем. логические: выдвижение гипотез и их обоснование
| Инициативное сотрудничество в совместном решении проблемы (задачи). Умение договариваться.
|
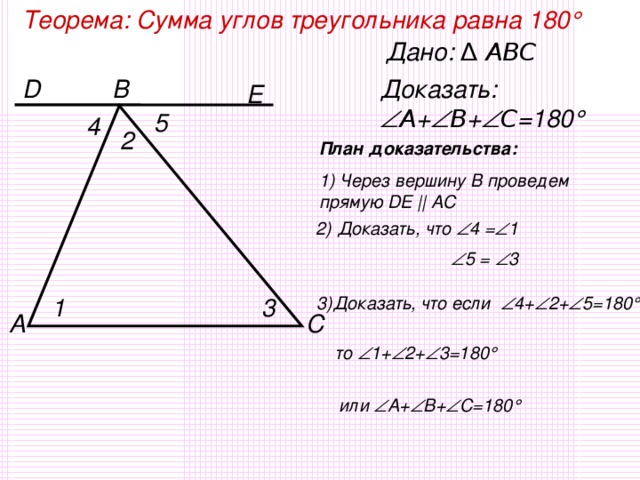
| V Изучение нового материала. Ведёт диалог с обучающимися класса, задает вопросы Предлагает обучающимся выделить условие и заключение теоремы, сделать чертеж и записать в тетрадях - что дано и что требуется доказать. Предлагает составить план доказательства и записать в тетрадях -Что надо сделать с гипотезой, чтобы убедиться, что она справедлива для любого треугольника? Как называется утверждение, справедливость которого надо доказать? Откройте учебник и найдите формулировку теоремы на с 70.
-Ребята, вы знаете, что в геометрии любое утверждение доказывается при помощи уже доказанных ранее фактов. Посмотрите внимательно на заключение теоремы. Нам необходимо доказать, что сумма углов треугольника равна 180°. А в каких, изученных ранее фактах, мы сталкивались с числом 180°? Слайд 8 -Так как смежные углы в сумме образуют развернутый угол, то предлагаю 1) и 2) варианты рассматривать как один факт: Развернутый угол равен 180°. -Кто-нибудь видит на нашем чертеже параллельные прямые? А можно их построить? -Давайте построим прямую а, проходящую через вершину В, параллельно стороне АС Дано: Δ АВС. Доказать: 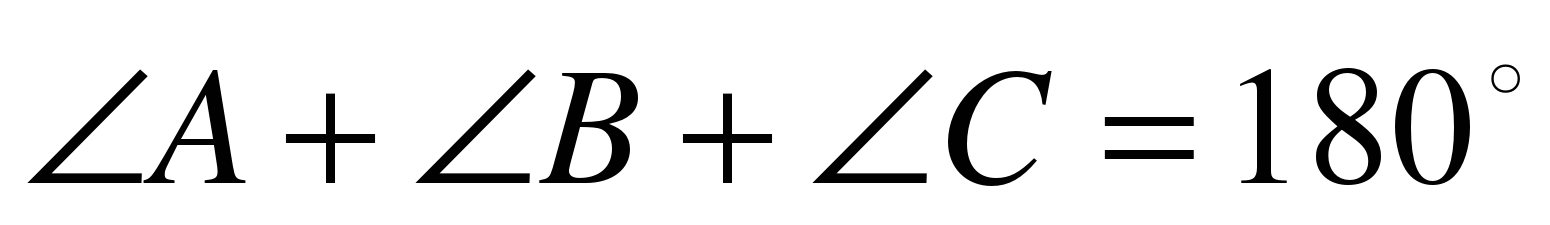 Доказательство: 1.Доп. построение: прямая а ǁ АС; 2.Доказать равенство углов 1 и 4, 3 и 5; 3.Найти сумму углов 2,4,5; (образуют развёрнутый угол) 4.Сделать вывод про сумму углов 1,2,3.Слайд Какое равенство мы получим в результате? -Что и требовалось доказать. После этого на экран выводится портрет Пифагора, как автора первого доказательства теоремы о сумме углов треугольника.
|
Отвечают на вопросы учителя, записывают в тетрадь доказательство теоремы
Надо доказать.
Теорема Читают формулировку теоремы. Возможные варианты ответов учащихся: 1)Развернутый угол равен 180° 2)Сумма смежных углов равна 180°. 3)Если две параллельные прямые пересечены третьей, то сумма односторонних углов равна 180°. 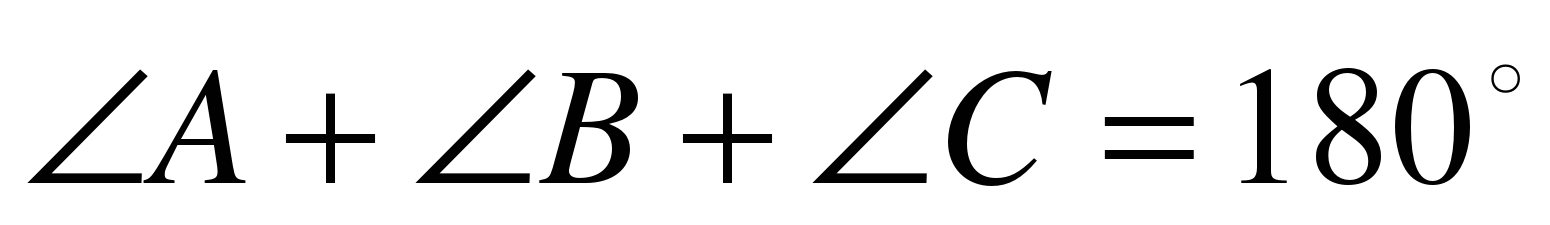
Записывают доказательство теоремы. | Поиск и выделение необходимой информации. Структурирование знаний. Анализ объектов.
| Логические: решение проблемы, построение логической цепи рассуждений, доказательство.
| Умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации
|
| VI Динамическая пауза - Знаете ли вы, что такое «царственная осанка»? Встаньте, попробуем принять царственную позу: спина прямая, мышцы головы без напряжения. Чтобы активизировать мозг, интенсивно массируем межбровную точку: указатель- ным пальцем правой руки делаем 5 круговых движений в одну сторону и в другую. Повторим это 2 – 3 раза. При помощи рук покажите прямой угол, тупой, острый. Поменяйте руки. Теперь покажите острый, прямой, тупой. Параллельные прямые (руки вверх), развёрнутый угол. Садитесь.
|
Из положения стоя, для разгрузки позвоночника, выполняют несколько упражнений, связанных с темой урока. |
|
|
|
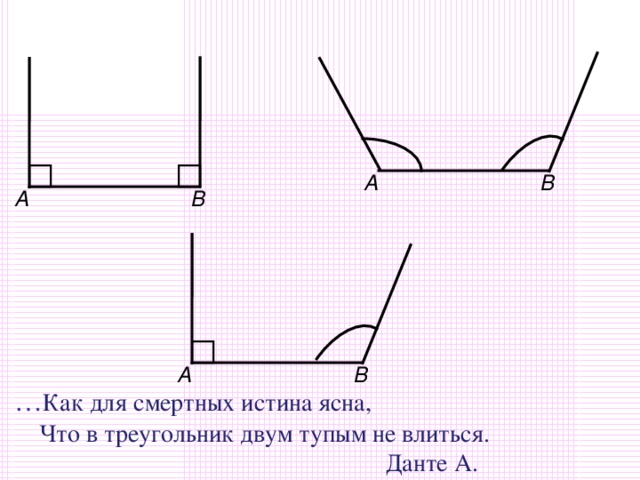
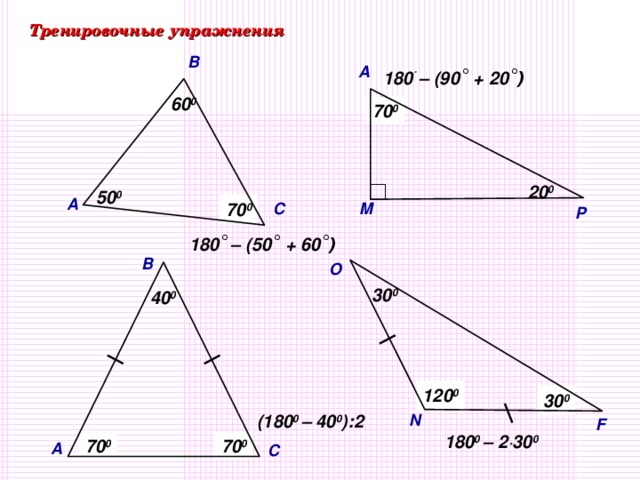
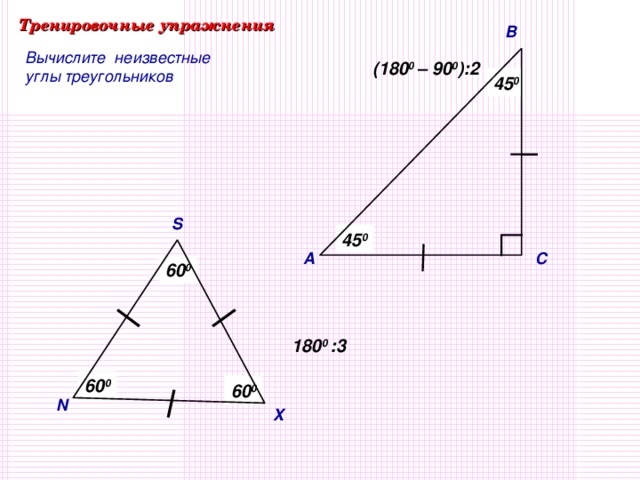
| VII Первичное закрепление нового материала Организует решение задач по готовым чертежам на применение теоремы. Организует самостоятельную работу с учебником. Обращает внимание обучающихся, для чего необходима новая теорема- чтобы находить угол треугольника, если известны два его угла или их сумма. -Вернемся к проблемному вопросу. Так в каком же треугольнике сумма углов больше? Трудно представить, что все треугольники: прямоугольные, остроугольные, тупоугольные, равнобедренные, равносторонние, большие, маленькие – имеют одну и ту же сумму углов. Вопросы. Слайд 9-10 Может ли треугольник иметь: а) два прямых угла б) два тупых углав) один прямой и один тупой угол? Объясните свой ответ, опираясь на изученную теорему. Из данной теоремы можно получить следствия. Сейчас прочитайте самостоятельно п.31 , найдите, что следует из теоремы. В любом треугольнике либо все углы острые, либо два острых угла, а третий тупой или прямой. Слайд 11 Какой треугольник называют остроугольным? Прямоугольным? Тупоугольным? Давайте вернемся к нашей схеме. Слайд 12 По какому признаку разбиты треугольники на группы? Что такое классификация? Перечертите схему в тетрадь. Может треугольник быть одновременно тупоугольным и равнобедренным? Прямоугольным и разносторонним? Для чего мы изучали теорему? Где нам пригодятся знания? Давайте решим несколько тренировочных упражнений на готовых чертежах. Как найти угол треугольника, если известны два его угла? Слайд 13-14 Чему равен угол равностороннего треугольника? Чему равны углы прямоугольного равнобедренного треугольника? Это тоже следствия из теоремы. Сделайте иллюстрации этих следствий в тетради. Ответьте на вопросы: Существует ли треугольник, у которого углы равны: 340, 560, 900 460, 1600, 40 750, 800, 250 1000, 200, 600 1200, 300, 150 Определите вид треугольника, если он существует. |
С места отвечают на вопросы.
Читают текст учебника Записывают следствие из теоремы в тетрадь.
Отвечают на вопросы.
Работают в тетради. Распределение по группам, разрядам, классам.
-Можем находить неизвестные углы треугольника.. Фронтально устно решают задачи с аргументацией каждого действия. Делают иллюстра -ции в тетради.
| Умение формулировать собственную точку зрения, высказывать и аргументировать ее), оформлять свои мысли в устной форме | Логические: выбор оснований и критериев классификации объектов;
| Планирование учебного сотрудничества с учителем и сверстниками, умение слушать и понимать речь других |
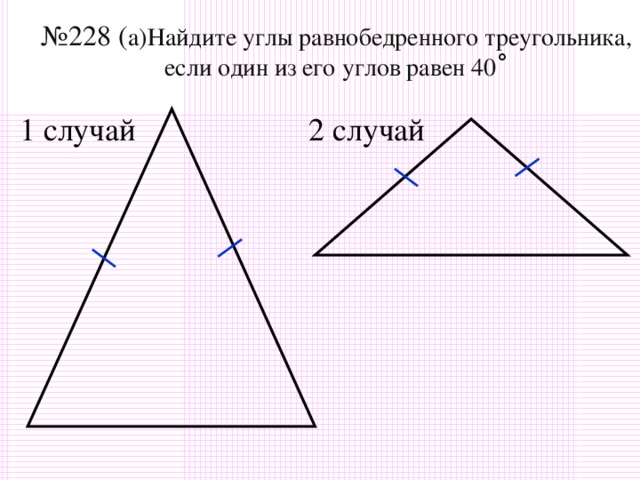
| VIII Организация первичного контроля Организует групповую работу по решению задачи из учебника. Наблюдает за работой детей. Помогает, при необходимости проверяет ответы. Комментирует ход решения. Слайд 15 -Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. (Д. Пойа) Давайте решать задачи. Решите задачу № 228(а) Сколько случаев надо рассмотреть? Кто справился с выполнением данной задачи Проводит первичную проверку знаний обучающихся в формате теста -достижения. -А сейчас вспомним про «царственную осанку», соберёмся с мыслями и приступим к ответам на вопросы теста. Организует взаимопроверку по готовым ответам. Слайд 16 Выставляет оценки. -У кого нет ошибок? Кто выполнил все верно? Какие затруднения возникли?
|
Обсуждают решение в группе, дают ответ, сверяют с образцом решения.
Самостоятельно вписывают в предложенные задания ответ.
| Оценка-осознание уровня и качества усвоения; контроль | Рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности;
| Планирование способов взаимодействия |
| IX Подведение итогов на рефлексивной основе, выставление оценок. Ведёт диалог с обучающимися класса, задает вопросы. Предлагает оценить свою работу на уроке, ответить на вопросы. - Какую цель мы перед собой поставили? - Почему возникла необходимость в доказательстве этого утверждения? - Что мы использовали при доказательстве теоремы? - Мы достигли цели? А теперь оцените свою работу на уроке. 1.Я всё понял на уроке, доволен своей работой. 2.Я понял теорему, но допускал ошибки. 3.Я не разобрался с новым материалом, нужна помощь. -Как вы думаете достаточно одного урока для понимания этой темы? Если нет, то почему? Итак, ребята этот урок пополнил ваши знания о треугольнике, но это еще не предел. На следующих уроках мы продолжим изучение треугольников, и вы узнаете еще много интересного и познавательного об этой геометрической фигуре. X Домашнее задание Дает комментарий к домашнему заданию.- § 30, 31 выучить док-во теоремы № 223(а, б),228 №229 (по желанию)Учитель благодарит обучающихся за внимание и активную работу на уроке. |
Проводят самооценку, рефлексию.
Поднимают руку, если согласны с утверждением. -Нет. - Рассуждают. Записывают домашнее задание в дневник | Умение оценивать учебные действия в соответствии с поставленной задачей. | Саморегуляция для повышения мотивации учебной деятельности | Умение осознанно и произвольно строить речевое высказывание в устной форме. |
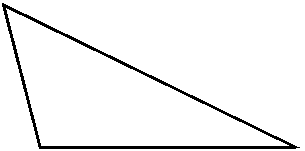 В
В 
 В
В
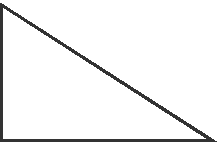 айдите сумму внутренних углов каждого треугольника.
айдите сумму внутренних углов каждого треугольника.