Урок геометрии в 7 классе
« Треугольник есть фигура,
которая не может разложиться в другой вид
более простой фигуры (между тем как, наоборот,
четырехугольник разлагается на треугольники)
и поэтому есть первый фундамент
всякой вещи, имеющей границу и фигуру»
Дж. Бруно
Тема: Сумма углов треугольника
Цели:
Формировать умение доказывать теорему о сумме углов треугольника, решать простейшие задачи по данной теме.
Развивать универсальные логические действия: сравнение, анализ, выдвижение гипотез, их обоснование, установление причинно-следственных связей, построение логических цепочек рассуждений, проведение доказательств; умение ставить цель и планировать её; умение осуществлять культурную коммуникацию с учителем и со сверстниками, работая в группе и в паре. Развивать навыки контроля и самоконтроля, прививать навыки по сохранению и укреплению своего здоровья.
Воспитывать целеустремленность, способность преодолевать трудности при решении учебной задачи.
Технологии, применяемые на уроке:
Элементы технологии развития критического мышления.
Технология учебной дискуссии.
Технология проблемного обучения.
Здоровьесберегающие технологии.
Информационно - коммуникативные технологии.
Оборудование:
Мультимедийный проектор.
Чертежные инструменты.
Формы работы с учащимися:
Фронтальная.
Работа в парах.
Самостоятельная работа.
Тип урока: Формирование новых знаний.
Ход урока:
Орг. Момент.
- Здравствуйте, ребята!
-Садитесь.
-Девизом сегодня на уроке будут слова
« Вдохновение нужно в геометрии
не меньше, чем в поэзии »
А.С.Пушкин
Поэтому я уверена, что сегодня на уроке не будет наблюдателей, а все будут активны.-Сначала мы вместе восхитимся глубокими знаниями – повторим все что нам известно о треугольниках, параллельных прямых
Затем постараемся пополнить знания о треугольниках, потренируем мозги. И, наконец, посмотрим, пополнилась ли наша копилка знаний.
Актуализация знаний учащихся (игровые технологии, ИКТ, технология уровневой дифференциации).
Да, путь познания не гладок,
Но знаем мы со школьных лет,
Загадок больше, чем отгадок,
И поискам предела нет.
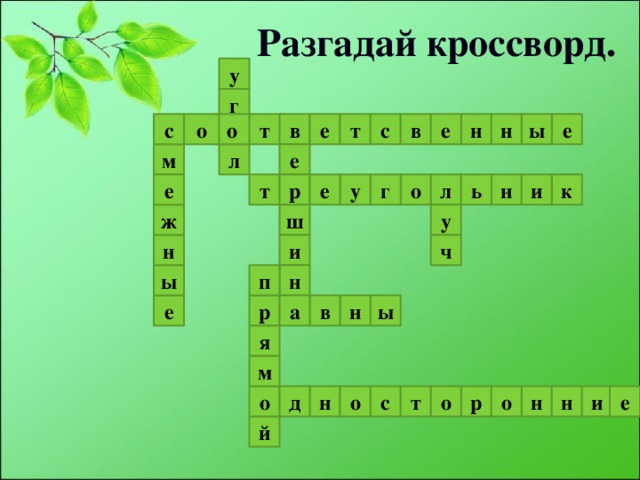
В форме небольшой викторины по рядам класса проводится игра «Разгадай кроссворд». Ведет игру учащийся).
Слайд № 4 презентации

Вопросы к кроссворду:
По горизонтали:
1. Если эти углы равны, то прямые параллельны.
2. Геометрическая фигура из двух лучей выходящих из одной точки….
3. Углы, сумма которых равна 180°
4. Если прямые параллельны. То накрест лежащие углы …
По вертикали:
1. Геометрическая фигура, которая состоит двух лучей, исходящих из одной точки.
2. Угол равный 90° …
3. Часть прямой, имеющая начало, но не имеющая конца…
4. Точка, из которой выходят стороны треугольника…
5. Углы, сумма которых равна 180°
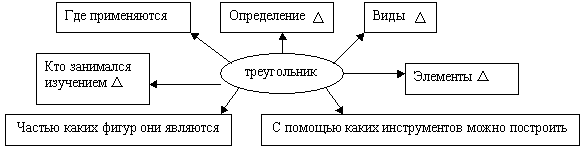
Обобщим наши знания: расскажем все, что мы знаем о треугольнике Слайд № 5 презентации
Эмоциональное включение учащихся в урок. Слайд № 4 презентации
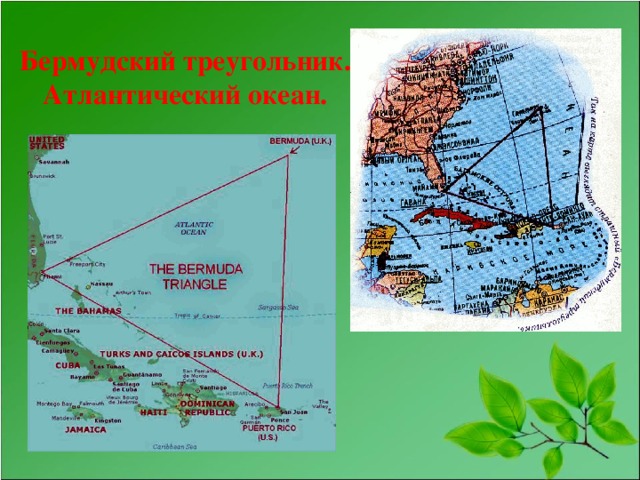
В Атлантическом океане есть место, по форме напоминающее геометрическую фигуру, о которой мы сегодня будем говорить. Это место, расположенное между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида и называется “бермудским треугольником”. А ещё его называют “дьявольский треугольник”, “треугольник проклятых”. Загадочность его заключается в том, что в нём бесследно исчезают корабли и самолёты. Природа “бермудского треугольника” остаётся тайной и по сей день. Ещё один общеизвестный треугольник – это «невозможный треугольник». Который увековечен в виде скульптуры в д. Опховен, Бельгия. И треугольник Пенроуза в городе Перт, Австралия.
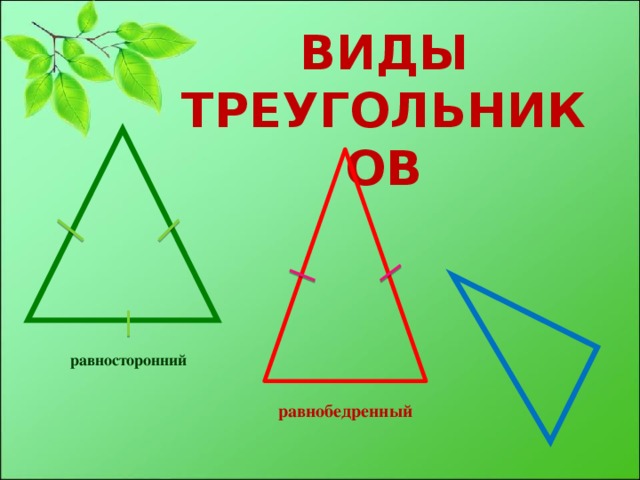
Но мы с Вами поговорим о ВОЗМОЖНЫХ треугольниках. Вспомним виды треугольни ков.
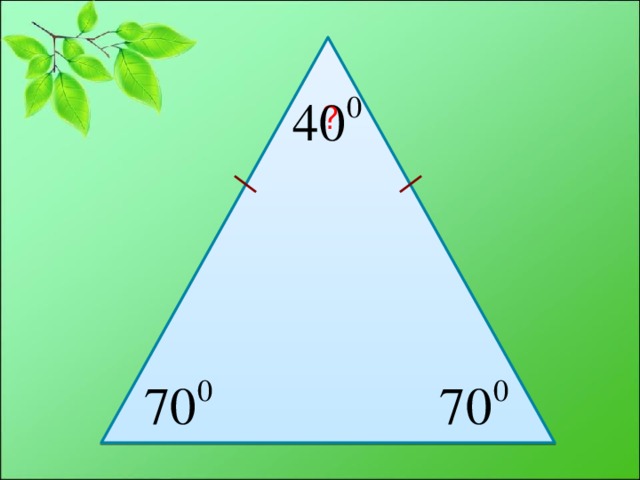
1. Какие треугольники мы знаем по отношению их сторон (равносторонние, равнобедрен ные, разносторонние). Слайд № 9 презентации
2. перечислим известные нам углы.
- Что называют углом?
Как называется угол, градусная мера которого 90, 180?
- Какой угол называется острым, тупым? Слайд №10 презентации
3.Изучение нового материала (проблемное обучение, частично-поисковый метод).
Объектом нашего внимания сегодня на уроке будут углы треугольника. Треугольники различаются и по углам. Постройте 1 ряд - острый, 2 ряд - тупой и3 ряд - прямой углы.- Достройте их до треугольника. - Попробуйте дать название этим треугольникам по их углам
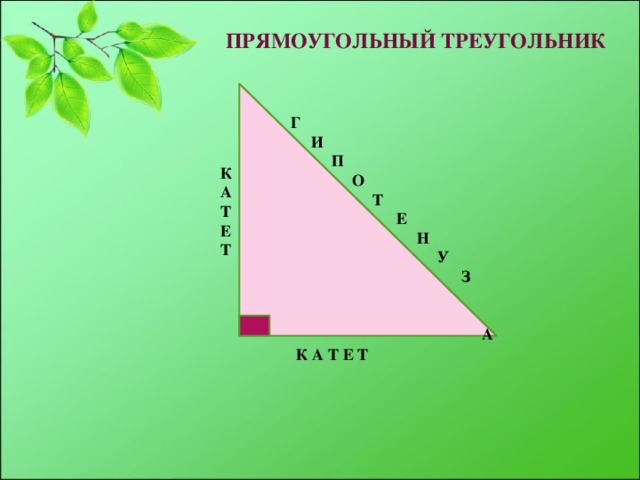
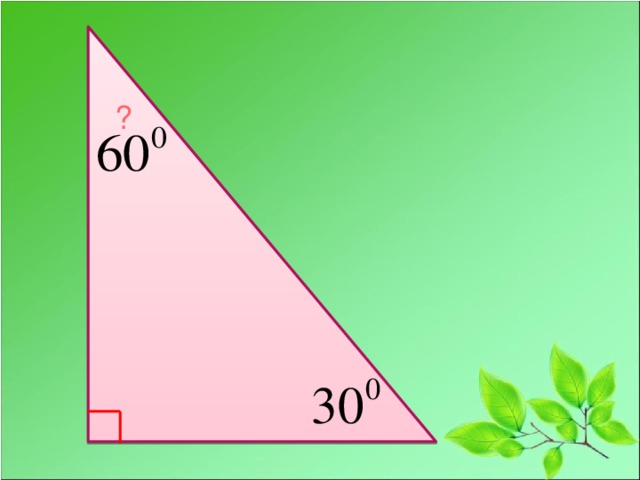
Прямоугольный треугольник. Его стороны имеют особое название
Слайд №11-12презентации.
Проблемная ситуация.
Из моделей углов построить треугольник ( на партах модели тупого, острого и пря-мого угла).
Учащимся предлагается практическая задача: с помощью транспортира построить произвольный равносторонний треугольник. Равносторонний →равнобедрен ный→два угла равны→все углы равны. Возникает проблема: нужно знать сумму внутренних углов треугольника. Слайд №13презентации.
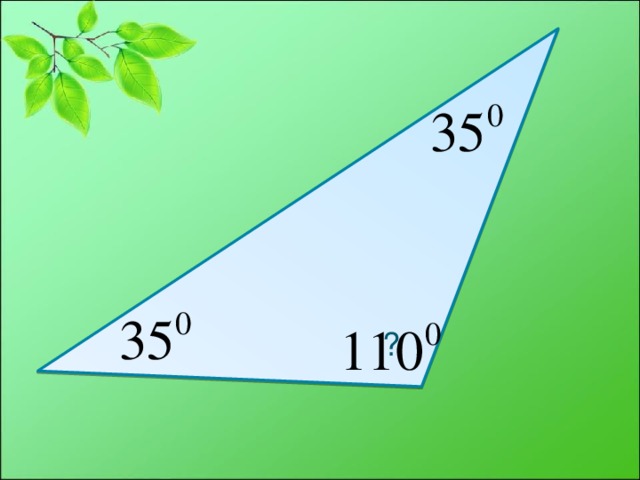
Итак, о треугольнике мы знаем уже достаточно много. А как вы думаете, чему равна сумма углов любого треугольника? Слайд №14презентации (Заслушать ответы). Давайте проверим, верны ли ваши предположения с помощью практической работы.
Практическая работа (способствует актуализации знаний и навыков самопознания). (Работа в парах.) Слайд №15-17 презентации.
- Ребята, очень часто ученые экспериментальным путем устанавливают важные факты. Это происходит в разных областях науки, например, в физике, в химии, и в геометрии тоже.
-Я вам тоже предлагаю побыть сегодня в роли исследователей. Работать будут у нас исследовательские лаборатории (работа в парах). (игровые технологии, уровневая дифференциация, ИКТ).
Итак, приступим к исследованиям (каждой паре раздаются планы работы – приложение, по три треугольника – остроугольный, тупоугольный, прямоугольный)
У каждого из вас есть на парте по одному треугольнику разных цветов. 1 ряд измерьте каждый угол треугольника с помощью транспортира, найдите сумму углов (на партах треугольники разных цветов – тупоугольные, прямоугольные и остроугольные)
Я предлагаю найти сумму углов треугольника двумя другими способами: возьмите треугольники, которые лежат у вас на парте. Они желтого или розового цвета. Обозначьте углы треугольника числами 1, 2, 3.
Учащиеся с желтыми треугольниками: оторвите два угла треугольника и приложите их к сторонам третьего угла так, чтобы все вершины были в одной точке. Замечаем, что все углы треугольника в сумме образуют развернутый угол.
Учащиеся с розовыми треугольниками: сложите углы во внутрь треугольника. Заметим, что перегибать треугольник надо по прямой параллельной к стороне, того угла который мы будем сгибать первым, а данный угол должен касаться данной стороны. Замечаем, что все углы треугольника в сумме образуют развернутый угол.
- Чему равна градусная мера развернутого угла?
- К какому выводу мы пришли?
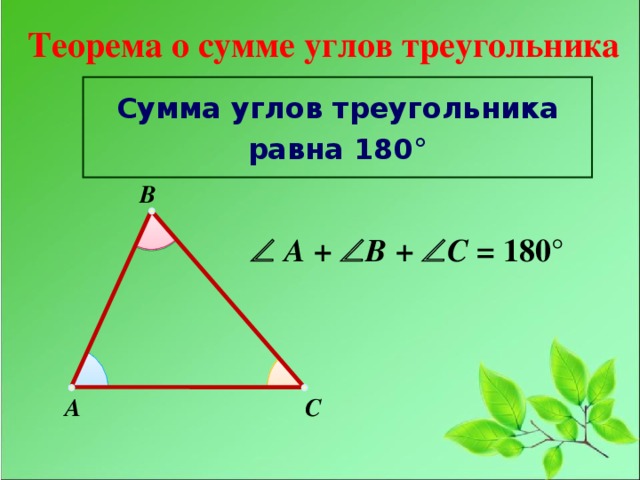
- Сумма углов треугольника равна 180 градусов.
Выполнив практическую работу, мы установили, что сумма углов треугольника равна 180 градусов.
В математике практическая работа дает возможность лишь сделать какое-то утверждение, но его нужно доказать. Утверждение, справедливость которого устанавливается путем доказательства, называется теоремой.
Какую теорему нам нужно доказать?
Сумма углов треугольника равна 180 градусов.
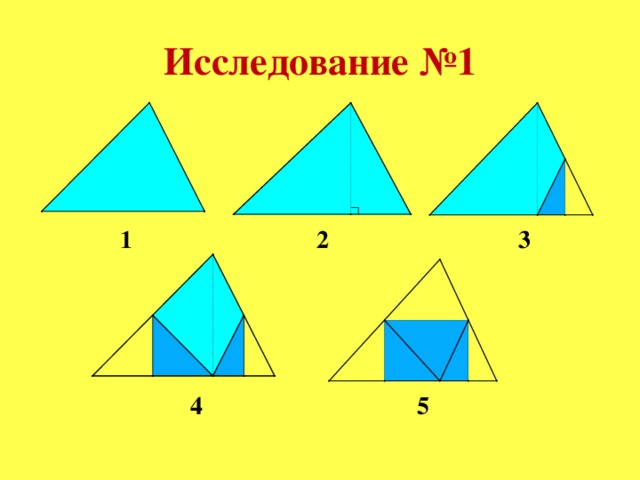
Исследование 1. Слайд № 15 презентации
План.
1. С помощью транспортира измерить углы треугольника.
2. Результат записать в таблицу.
3. Найти сумму углов.
4. Сообщить результат.
(Результат записывают в таблицы – приложение)
Перед работой обращает внимание на технику безопасности при работе с ножницами.
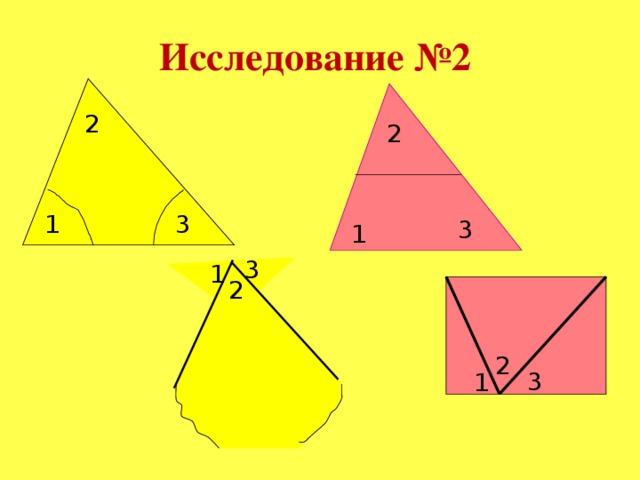
Исследование 2. Слайд № 16 презентации
План.
1. Отрезать ножницами все углы
2. Собрать их в одной точке
3.Ответить на вопрос: Что образовали углы?
4. Сделать вывод.
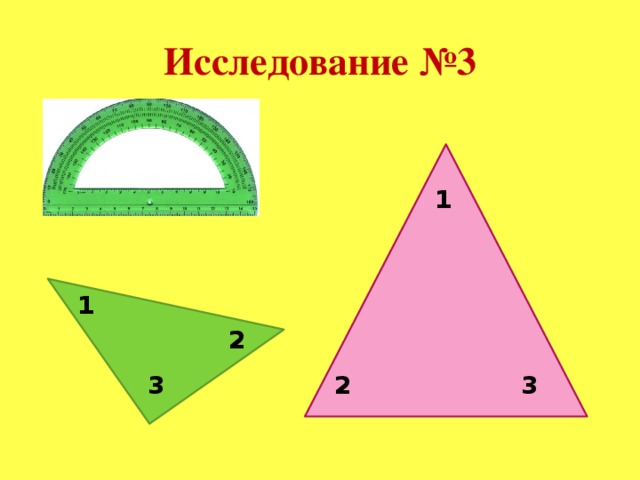
Исследование 3. Слайд №17 презентации
План.
1. Отогнуть один угол треугольника так, чтобы он касался противоположной стороны и линия сгиба была параллельна этой стороне.
2. Второй угол треугольника отогнуть так, чтобы он соприкасался с первым углом.
3. Аналогично отогнуть третий угол треугольника.
4. Сделать вывод.
Физминутка (здоровьесберегающие, игровые технологии).
Встаньте, поднимите руки вверх, потянитесь к звездам;
покажите развернутый угол,
прямой угол,
тупой угол,
острый угол.
-Молодцы! Садитесь
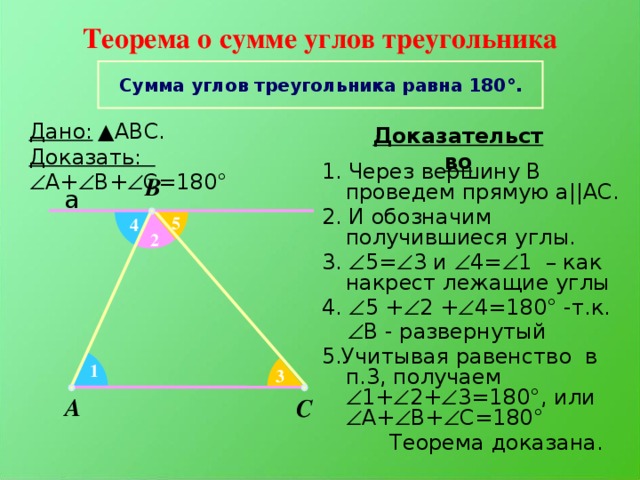
Доказательство теоремы Слайд №23-24 презентации
Историческая справка. Слайд №25 презентации
4. Первичное закрепление изученного
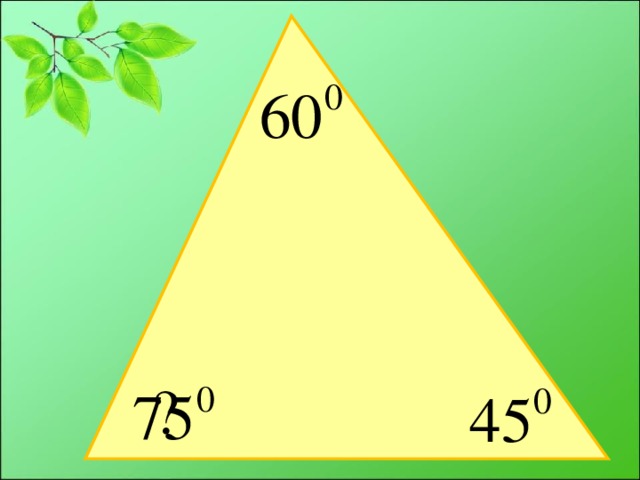
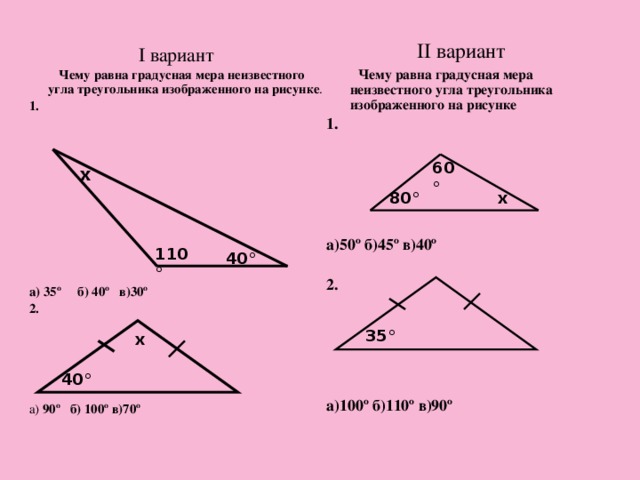
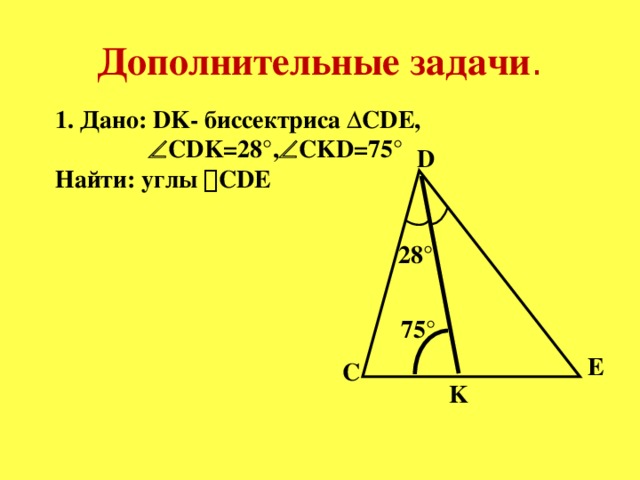
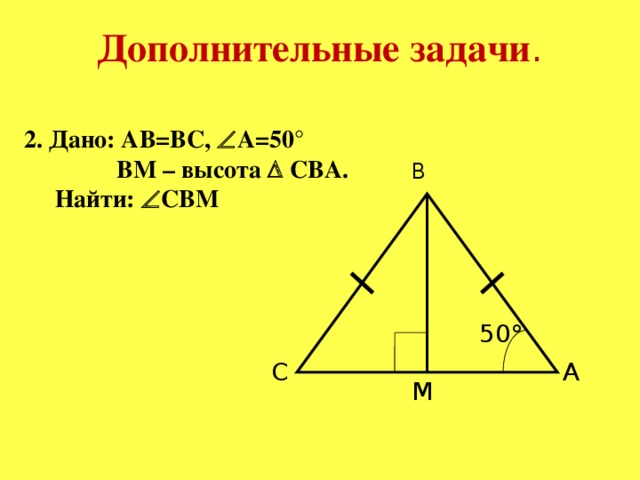
Решение задач по готовым чертежам Слайд № 26-30 презентации
5. Усвоение знаний. Решение задачи. Слайд № 31 презентации
6.Самостоятельная работа с взаимопроверкой Слайд № 32-33 презентации
7. Домашнее задание. Дифференцированное. Слайд № 34 презентации Сегодня на уроке мы показали различные способы доказательства одной теоремы – теоремы о сумме углов треугольника. При решении задач мы использовали и следствия из этой теоремы, а также повторили многие вопросы предшествующих тем: свойства смежных углов треугольника, признаки равенства треугольников, определение и свойства равнобедренного треугольника, свойства углов, образованных параллельными прямыми и секущей и другие факты. А на следующем уроке мы рассмотрим соотношения между сторонами и углами треугольника. Вы еще раз сегодня убедились в том, что предмет геометрии тесно связан с другими предметами.
Я благодарю всех учащихся, которые активно работали на уроке, все ответы будут оценены соответственно, также все учащиеся получат оценки по результатам тестирования.
Дома вам предстоит решить задачи, аналогичные тем, что были разобраны сегодня на уроке:
Карточки
ВАРИАНТ 1.
В треугольнике СДЕ с углом Е, равным 320, проведена биссектриса СК, 0. Найдите
В равнобедренном треугольнике MNP с основанием МР и углом N, равным 640, проведена высота МН. Найдите
ВАРИАНТ 2.
В треугольнике СДЕ проведена биссектриса СК, 0,0. Найдите
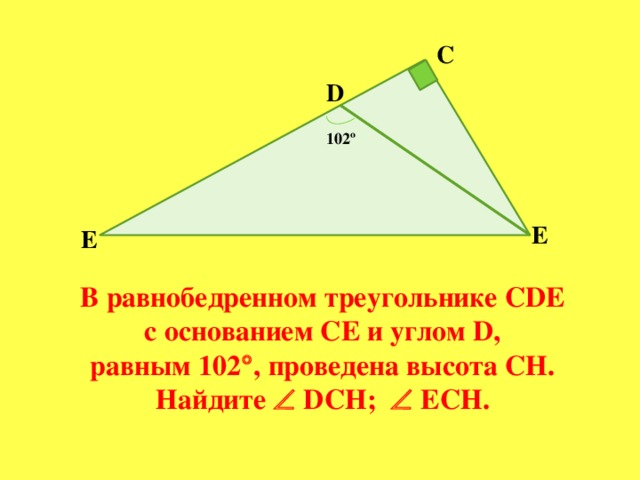
В равнобедренном треугольнике СДЕ с основанием СЕ и углом Д, равным 1020, проведена высота СН. Найдите
6. Итог урока. Рефлексия: Слайд № 41-42 презентации
Продолжите фразу:
“Сегодня на уроке я узнал…”
“Сегодня на уроке я научился…”
“Сегодня на уроке я познакомился…”
“Сегодня на уроке я повторил…”
“Сегодня на уроке я закрепил…”
Дополнительный материал.
Сказка: жили были три угла. И жили они в домике-треугольнике. В их доме температура всегда была ровно 180 градусов-это очень жарко, но градусы эти были не по Цельсию, а геометрические, которые они делили между собой, но не всегда поровну, зато обязательно всегда сумма была 180. И когда каждый из них спорил, кто главнее и больше, форма их дома- треугольника- менялась. Один из углов мог растянуться аж на 100 градусов, а иногда и больше. И тогда два других угла становились едва заметными. И эти два угла начинали драться, кто ж из них больше. Один мог быть 70, а другой тогда только 10. Или же они делились поровну по 40, например, градусов. Тогда их дом назывался равнобедренный)).Внутри кораблика из газеты он всегда прячется! Такой дом-треугольник очень устойчивый. Но только один из углов мог становиться прямым и быть 90 градусов, то есть занимать ровно половину всего их общего дома-треугольника! Тогда треугольник назывался прямоугольным, и если рядышком вдруг оказывался точь-в точь такой же треугольник-сосед , то вместе они могли стать тем самым равнобедренным. Прямоугольний треугольник при желании становился одновременно и равнобедренным, если другие углы делились по 45 градусов. А еще домик-треугольник мог быть правильным, когда все углы хорошо себя вели и не ссорились, они делили градусы поровну по 60 каждому. Тогда и все стороны домика быть равными и этот домик становился прямо-таки волшебным в стране, которая звалась Математика. Правильный треугольник всегда еще и равнобедренный, но никогда не прямоугольный! Но самое страшное, что может случиться с треугольником- это когда один угол-жадина захочет забрать все градусы себе! все 180! И тогда два других угла просто лопнут и исчезнут как мыльные пузыри! а домик растает и превратится в прямую линию! И не будет больше ни углов, ни домика. Поэтому никогда не надо жадничать, этому даже математика учит.)