Цели урока:
1. рассмотреть свойства прямоугольных треугольников;
2.научить решать задачи на применение свойств прямоугольных треугольников;
3.сформировать умение рассуждать по аналогии;
4.продолжить работу по развитию речи и мышления учащихся.
Оборудование: компьютеры, раздаточный материал (карточки с готовыми чертежами).
Ход урока:
1.Организационны момент:
а) сообщить классу тему урока и сформулировать его цели;
б) подготовка программ, необходимых для проведения занятия.
2.Актуализация знаний учащихся.
1)вспомнить определение прямоугольного треугольника;
2)Чему равна сумма всех углов в треугольнике;
3)Решить задачи по готовым чертежам.
Задачи представлены в виде презентации.
На этом этапе урока отрабатывается умение пользоваться программой Power Point.
Весь класс разбит на три группы (по 3 человека).
Всем учащимся раздаются готовые карточки с готовыми чертежами (приложение №1). После того, как будут решены все задачи, к доске выходят по одному представителю от группы, для защиты своего решения. Кроме того, внутри группы дается оценка каждому, кто принимал участие в решении задач и выставляется на листах с решением.
Цель решения данных задач – подготовить учащихся к изучению и доказательству свойств прямоугольных треугольников.
3.Объяснение нового материала.
1)Рассмотреть свойство10.
Использование этого свойства можно показать на примере решения задачи №265. Один учащийся решает у доски и комментирует все свои действия.
2) Доказательство свойств 20 и 30 следует провести учителю самому с записью условия и заключения прямого и обратного утверждений на доске в виде таблицы. Эту таблицу учащиеся должны воспроизвести в своих тетрадях.
4.Закрепление материала.
1) работа с программой Power Point;
Учащимся предлагается пройти тест (выбрав один из двух предложенных ответов). Тесты оформлены в виде презентации; предлагается закончить начатую фразу (проверяется на данном этапе, насколько уч-ся запомнили формулировки только что изученных свойств прямоугольных треугольников).
2)Решение задач по готовым чертежам.(Приложение №2, взаимопроверка)
Каждому учащемуся раздается лист с задачами. На этом листе учащиеся выполняют все расчеты, а затем обмениваются листами друг с другом и полученные ответы.
5.Физминутка.
3).Решение задачи из учебника №257 (один ученик работает у доски, остальные в тетрадях).
4)Самостоятельно решить задачи №259 и если останется время №260.
6.Подводится итог урока.
7.Домашнее задание (инструктаж).
1). 34, вопросы10,11.
2).№255,№256,№258.
Просмотр содержимого документа
«Рюмина С.А. геометрия 7 класс . Прямоугольные треугольники.»
Разработал:
Рюмина Светлана Анатольевна,
Учитель математики МКОУ сош №21 г.Бакал, первая категория.
Используемый учебник: Геометрия . 7 – 9: учебник для общеобразовательных учреждений / Л.С. Атанасян, В. Ф. Бутусов, С.Б.Кадомцев и др. - М. : Просвещение, 2012.
Оборудование для урока: АРМ учителя.
Тема урока: Прямоугольные треугольники.
Цели урока:
1. рассмотреть свойства прямоугольных треугольников;
2.научить решать задачи на применение свойств прямоугольных треугольников;
3.сформировать умение рассуждать по аналогии;
4.продолжить работу по развитию речи и мышления учащихся.
Оборудование: компьютеры, раздаточный материал (карточки с готовыми чертежами).
Ход урока:
1.Организационны момент:
а) сообщить классу тему урока и сформулировать его цели;
б) подготовка программ, необходимых для проведения занятия.
2.Актуализация знаний учащихся.
1)вспомнить определение прямоугольного треугольника;
2)Чему равна сумма всех углов в треугольнике;
3)Решить задачи по готовым чертежам.
Задачи представлены в виде презентации.
На этом этапе урока отрабатывается умение пользоваться программой Power Point.
Весь класс разбит на три группы (по 3 человека).
Всем учащимся раздаются готовые карточки с готовыми чертежами (приложение №1). После того, как будут решены все задачи, к доске выходят по одному представителю от группы, для защиты своего решения. Кроме того, внутри группы дается оценка каждому, кто принимал участие в решении задач и выставляется на листах с решением.
Цель решения данных задач – подготовить учащихся к изучению и доказательству свойств прямоугольных треугольников.
3.Объяснение нового материала.
1)Рассмотреть свойство10.
Использование этого свойства можно показать на примере решения задачи №265. Один учащийся решает у доски и комментирует все свои действия.
2) Доказательство свойств 20 и 30 следует провести учителю самому с записью условия и заключения прямого и обратного утверждений на доске в виде таблицы. Эту таблицу учащиеся должны воспроизвести в своих тетрадях.
|
| Теорема | Обратная теорема |
| Дано |
|
|
| Докажите |
|
|
| Доказательство |
|
|
4.Закрепление материала.
1) работа с программой Power Point;
Учащимся предлагается пройти тест (выбрав один из двух предложенных ответов). Тесты оформлены в виде презентации; предлагается закончить начатую фразу (проверяется на данном этапе, насколько уч-ся запомнили формулировки только что изученных свойств прямоугольных треугольников).
2)Решение задач по готовым чертежам.(Приложение №2, взаимопроверка)
Каждому учащемуся раздается лист с задачами. На этом листе учащиеся выполняют все расчеты, а затем обмениваются листами друг с другом и полученные ответы.
5.Физминутка.
3).Решение задачи из учебника №257 (один ученик работает у доски, остальные в тетрадях).
4)Самостоятельно решить задачи №259 и если останется время №260.
6.Подводится итог урока.
7.Домашнее задание (инструктаж).
1). 34, вопросы10,11.
2).№255,№256,№258.
Приложение №2.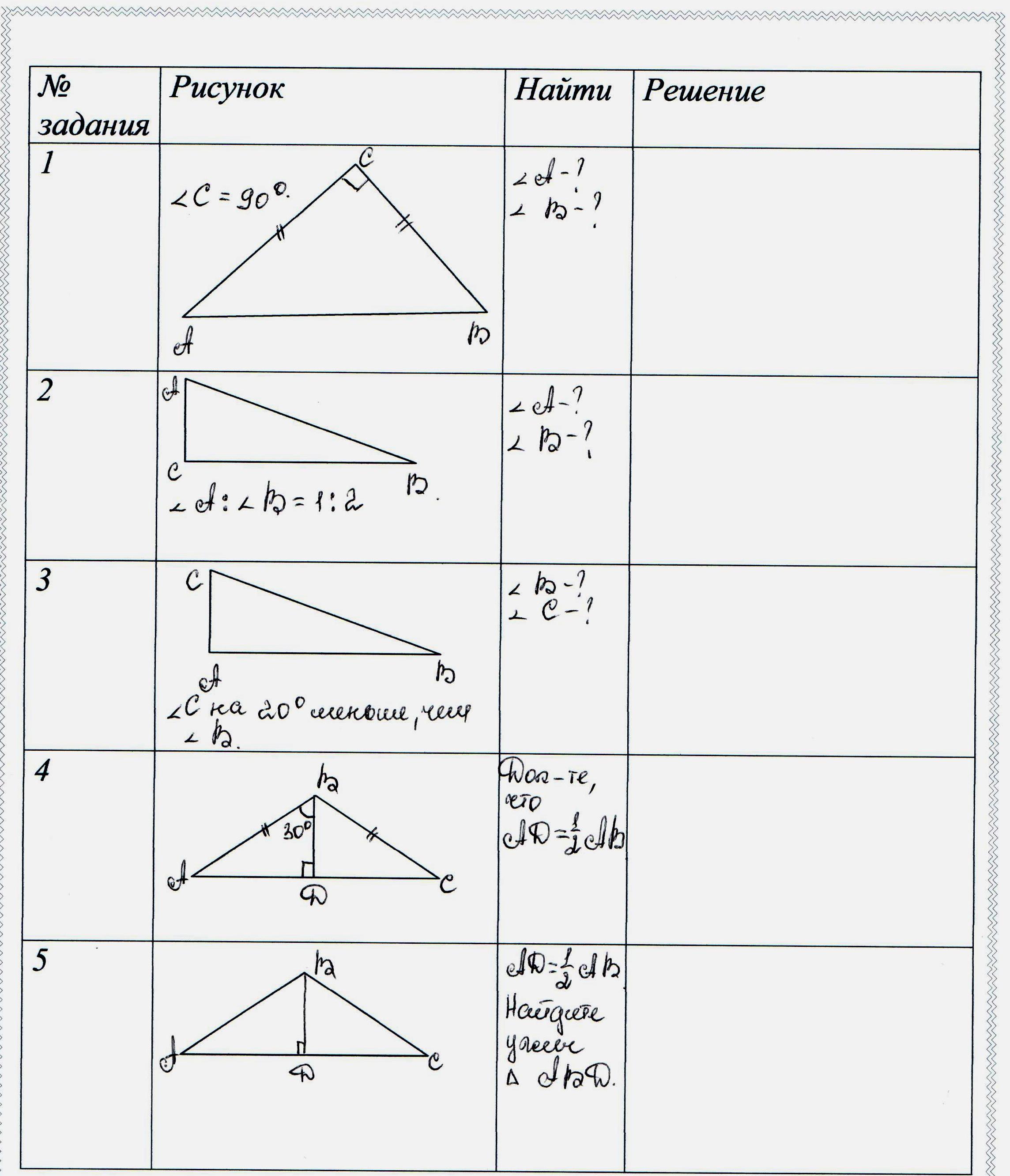
Приложение №1.
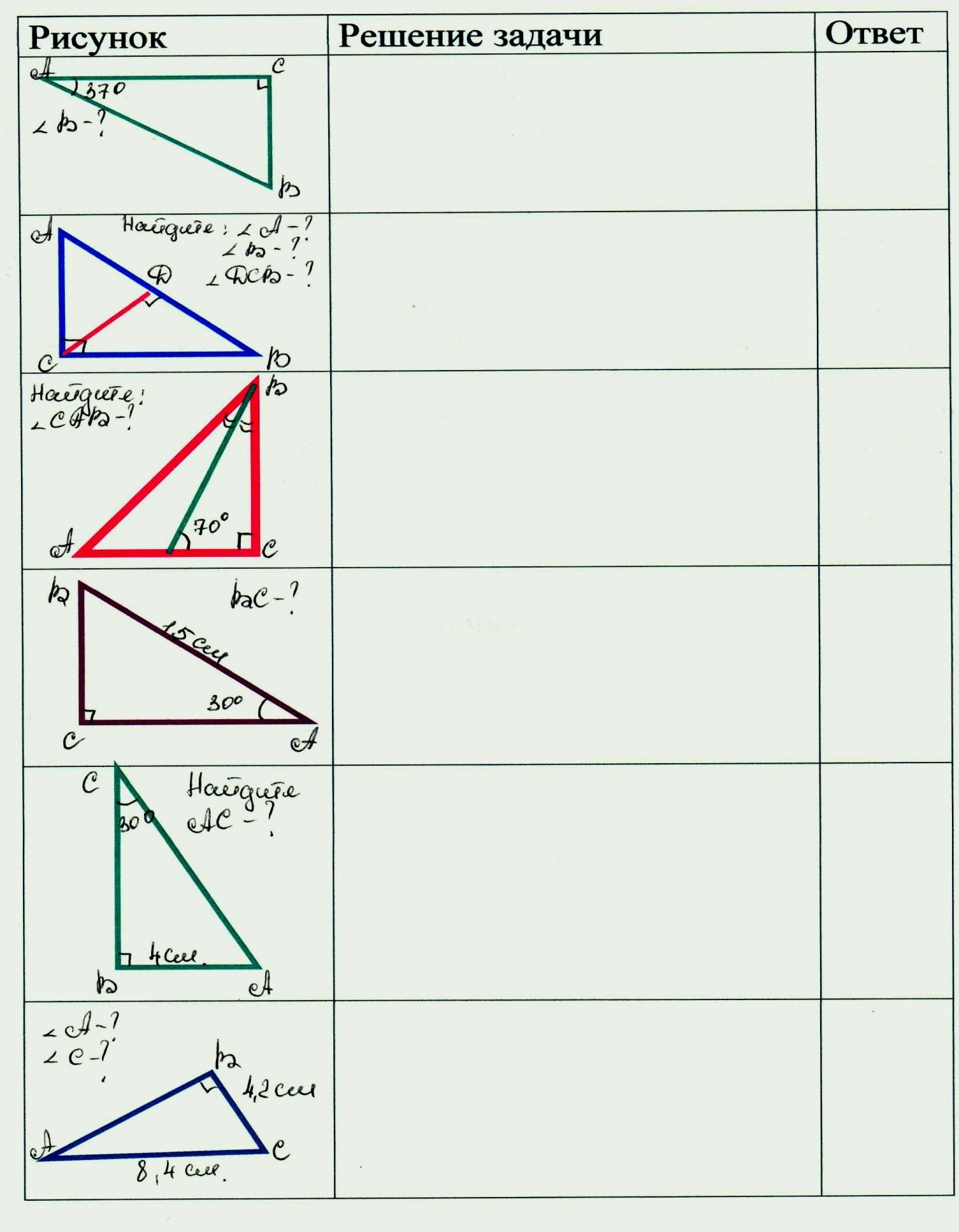
Просмотр содержимого презентации
«Геометрия прямоугольные треугольники»

Учитель математики:
Рюмина С.А.
МКОУ сош№21.

План:
1. Свойства прямоугольных треугольников.
2. Признаки равенства прямоугольных треугольников.
3. Теоремы.
4. Устная работа.
5 . Тренажер по геометрии
6. Теорема Пифагора.
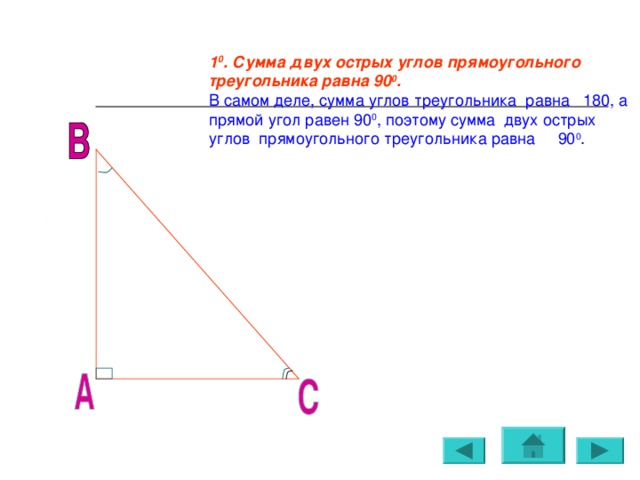
1 0 . Сумма двух острых углов прямоугольного треугольника равна 90 0 .
В самом деле, сумма углов треугольника равна 180, а прямой угол равен 90 0 , поэтому сумма двух острых углов прямоугольного треугольника равна 90 0 .
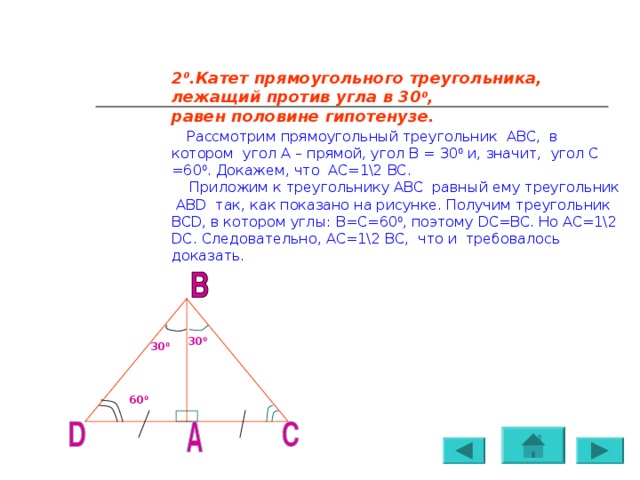
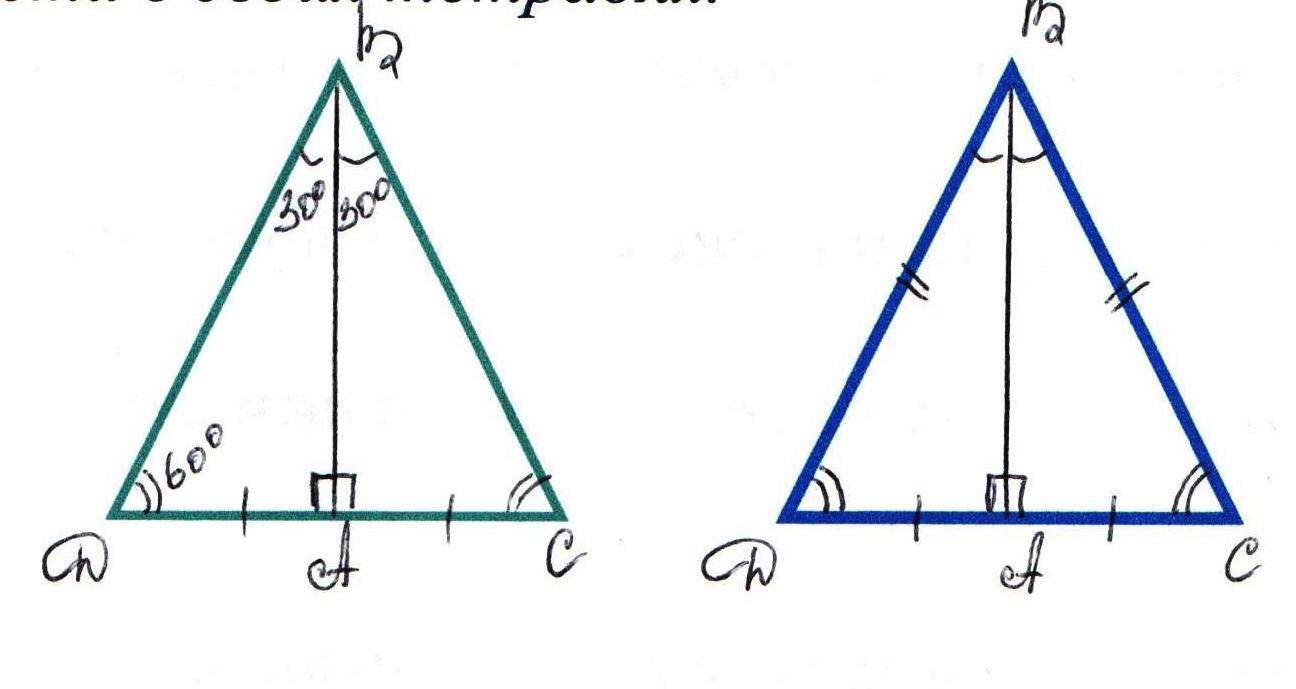
2 0 .Катет прямоугольного треугольника, лежащий против угла в 30 0 ,
равен половине гипотенузе.
Рассмотрим прямоугольный треугольник АВС, в котором угол А – прямой, угол В = 30 0 и, значит, угол С =60 0 . Докажем, что АС=1\2 ВС.
Приложим к треугольнику АВС равный ему треугольник АВ D так, как показано на рисунке. Получим треугольник BCD , в котором углы: В=С=60 0 , поэтому DC=BC . Но АС=1\2 DC . Следовательно, АС=1\2 ВС, что и требовалось доказать.
30 0
30 0
60 0
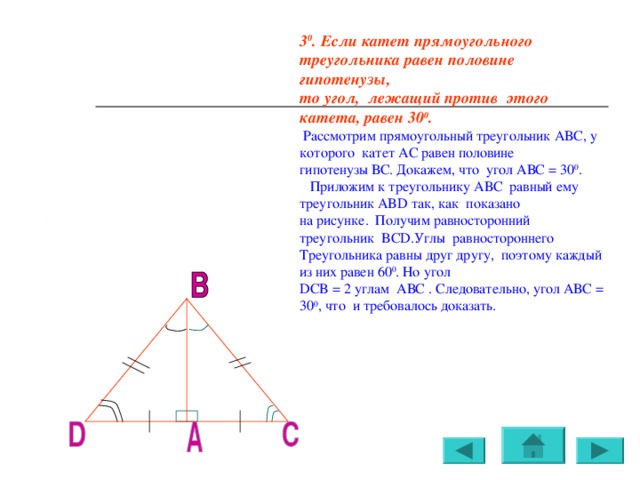
3 0 . Если катет прямоугольного треугольника равен половине гипотенузы,
то угол, лежащий против этого катета, равен 30 0 .
Рассмотрим прямоугольный треугольник АВС, у которого катет АС равен половине
гипотенузы ВС. Докажем, что угол АВС = 30 0 .
Приложим к треугольнику АВС равный ему треугольник ABD так, как показано
на рисунке. Получим равносторонний треугольник BCD .Углы равностороннего
Треугольника равны друг другу, поэтому каждый из них равен 60 0 . Но угол
DCB = 2 углам АВС . Следовательно, угол АВС = 30 0 , что и требовалось доказать.

Признаки равенства прямоугольных треугольников.
- Так как в прямоугольном треугольнике угол между двумя катетами прямой, а любые два прямых угла равны, то из первого признака равенства треугольников следует: если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны . Далее из второго признака равенства треугольников следует: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого, то такие треугольники равны.
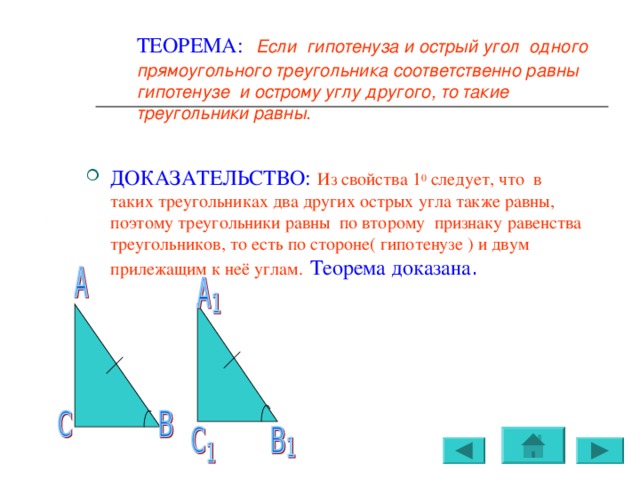
ТЕОРЕМА: Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- ДОКАЗАТЕЛЬСТВО: Из свойства 1 0 следует, что в таких треугольниках два других острых угла также равны, поэтому треугольники равны по второму признаку равенства треугольников, то есть по стороне( гипотенузе ) и двум прилежащим к неё углам. Теорема доказана .

ТЕОРЕМА: Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
- ДОКАЗАТЕЛЬСТВО: Рассмотрим треугольник АВС и А 1 В 1 С 1, у которых углы С и С 1 – прямые, АВ=А 1 В 1 ,ВС=В 1 С 1 . Докажем, что треугольники АВС=А 1 В 1 С 1 .Так как угол С = углу С 1 , то треугольник АВС можно наложить на треугольник А 1 В 1 С 1 так, что вершина С сместится с вершиной С 1 , а стороны СА и СВ наложатся соответственно на лучи С 1 А 1 и С 1 В 1 . Поскольку СВ=С 1 В 1 , то вершина В совместится с вершиной В 1 . Но такие вершины А и А 1 также совместятся. В самом деле, если предположить, что точка А совместится с некоторой другой точкой А 2 луча С 1 А 1 , то получим равнобедренный треугольник А 1 В 1 А 2 , в котором углы при основании А 1 А 2 не равны. Но это невозможно, поэтому вершины А и А1 совместятся. Следовательно, полностью совместятся треугольники АВС и А1В1С1 и, значит, они равны. Теорема доказана.

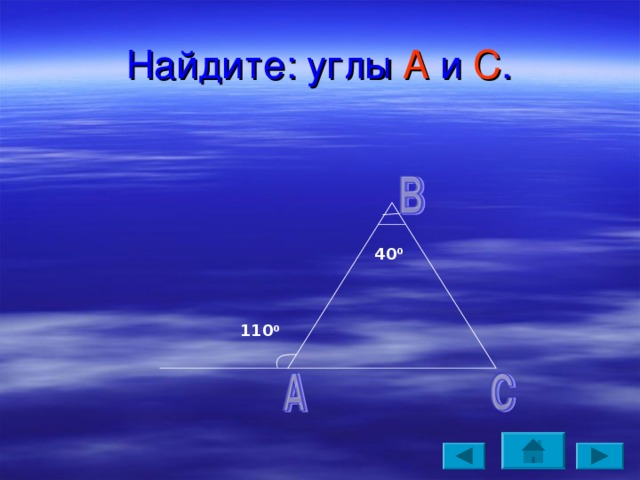
Найдите: углы А и С .
40 0
110 0

Найти: углы В и А
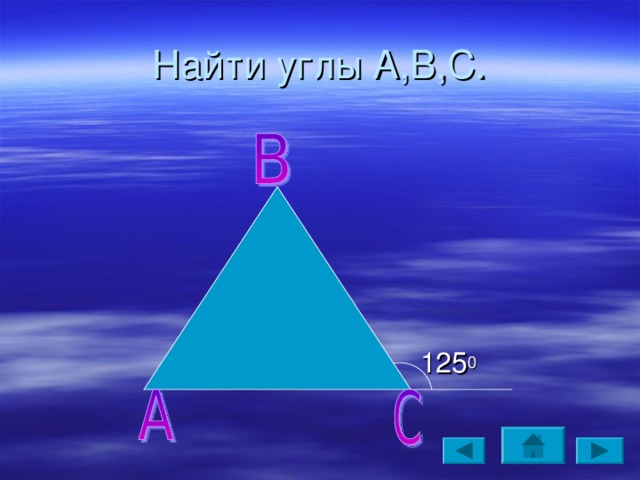
Найти углы А,В,С.
125 0
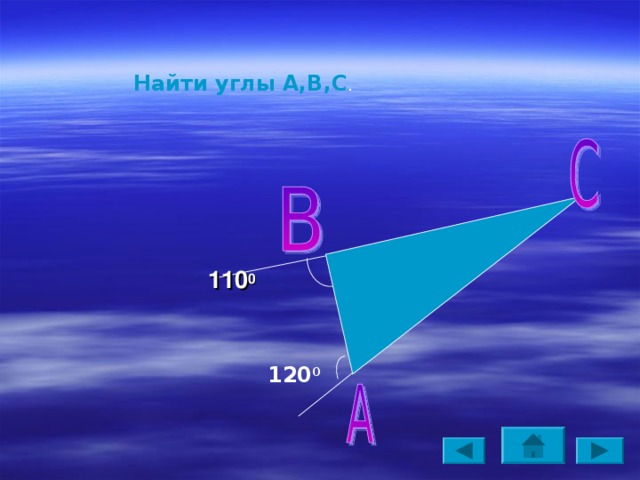
Найти углы А,В,С .
110 0
120 0

Найти углы А,В,С.
85 0
40 0
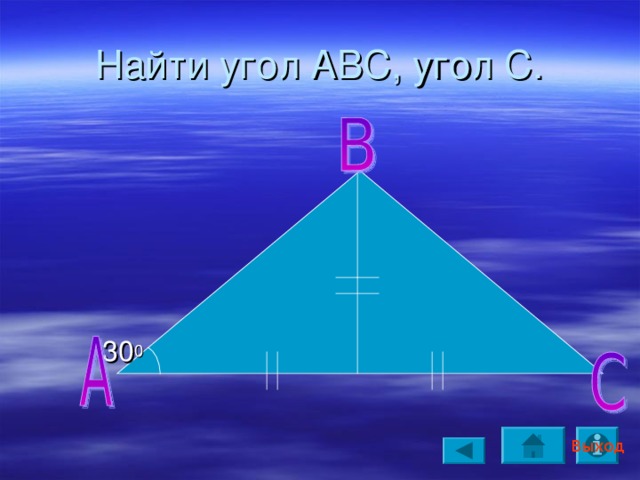
Найти угол АВС, угол С.
30 0
Выход


Нажми сюда, для выполнения теста .
















Нажми сюда, что бы выйти из программы.




















Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. (Пифагоровы штаны во все стороны равны)
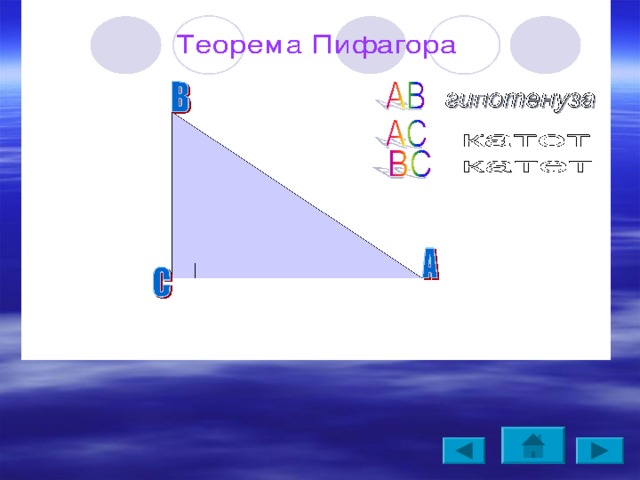
Теорема Пифагора
Площадь квадрата, построенного на гипотенузера, равна сумме площадей квадратов, построенных на катетах. (Пифагоровы штаны во все стороны равны)
Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
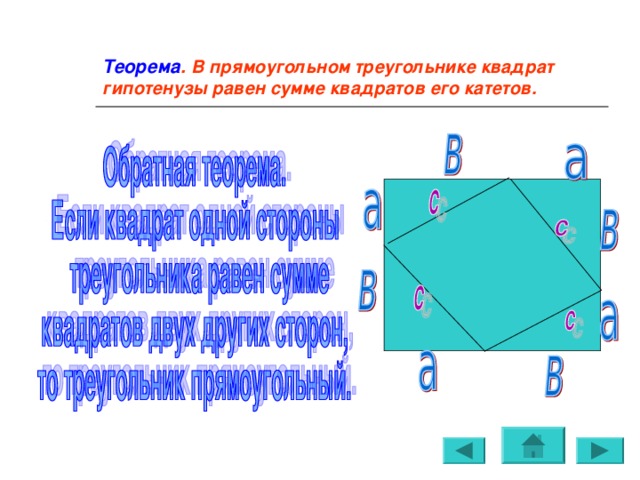
Теорема Пифагора

Площадь квадрата, построенного на гипотенузера, равна сумме площадей квадратов, построенных на катетах. (Пифагоровы штаны во все стороны равны)
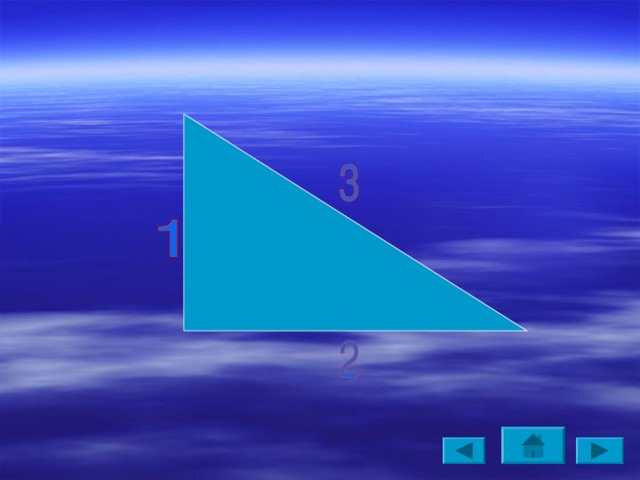
Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.

Теорема . В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.

Составьте по рисунку верное равенство, используя теорему Пифагора.


Арифметика. Леонтий Филиппович Магницкий . Случися некому человеку к стене лествецу прибрати, стены же тоя высота есть 117 стоп, и обрете лествецу долготою 125 стоп и ведоти хощет, колико стоп сея лествецы нижний конец от стены отстояти имать.
Просмотр содержимого презентации
«Тест по геометрии.»



































































































