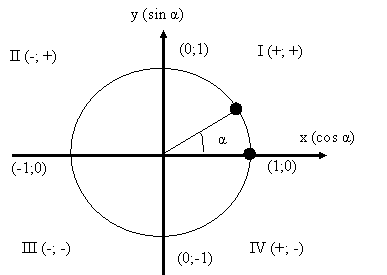Конспект урока " Формулы приведения" предназначен для учащихся 9 класса. В ходе урока закрепляется предыдущая тема: свойства тригонометрических функций, опеделение принадлежности угла четвертям единичной окружности, определение знака функции. Учащиеся работают с индивидуальным пособием " Числовой круг". Осуществляется обратная связь. Объясняется новый материал. Закрепление материала строится строго по алгоритму:1). определяем меняется функция на кофункцию или нет; 2). по исходной функции определяем знак.Работая над развитием грамотной матматической речи, проводим комментированную работу по цепочке.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Конспект урока алгебры " Формулы приведения"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Конспект урока алгебры " Формулы приведения" »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1790 руб.
2560 руб.
1970 руб.
2820 руб.
1760 руб.
2510 руб.
1970 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства