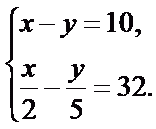Предмет: Алгебра Класс: 7
Базовый учебник Алгебра 7 класс, А. Г. Мордкович.: Мнемозина
Учитель: Репина А. Б.
Тема урока: Системы линейных уравнений с двумя переменными. как математические модели реальных ситуаций.
Цели урока:
- Познакомить учащихся с применением систем линейных уравнений при решении задач.
- Сформировать умение использовать системы уравнений при решении задач.
- Формирование умения переносить знания в новую ситуацию;
- Воспитать ответственность, самостоятельность, аккуратность при оформлении заданий.
Тип урока: изучение нового материала
План урока:
- Организационный момент
- Актуализация опорных знаний
- Изучение нового материала
- Закрепление. Формирование практических навыков при решении задач
- Самостоятельная работа. Самопроверка.
- Домашнее задание.
- Итог. Рефлексия.
Необходимое оборудование: компьютер, проектор.
План - конспект УРОКА
№
Этап урока
Деятельность учителя
Деятельность ученика
Формируемые УУД
Вводно-мотивационная часть урока(5 мин)
1
Организационный момент.
Цель – включить обучающихся в учебную деятельность, определить содержательные рамки урока, создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность.
- Ребята, сегодня на урок я хотела бы начать словами А. Эйнштейна: "Мне приходится делить своё время между политикой и уравнениями. Однако уравнения, по моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно."
- Как вы думаете, чем мы будем заниматься на уроке?
-Хорошо. -Где же применяются системы уравнений?
Итак, мы начнем рассматривать задачи, решить которые можно с помощью систем уравнений с двумя переменными. Сформулируйте цели урока.(научиться решать задачи с помощью систем уравнений)
- Чтобы продолжить работу, запишите в тетради тему урока. (на доске открывается тема урока)
Приветствует учителя, проверяют подготовку рабочих мест.
Отвечают на вопросы учителя, высказывают свои предположения.
Личностные: самоопределение, смыслообразование.
Регулятивные: планирование, целеполагание, волевая саморегуляция.
Познавательные: анализ, сравнение, самостоятельное выделение и формулирование познавательной деятельности, цели.
Коммуникативные: планирование учебного сотрудничества, выражение своих мыслей, аргументация своего мнения.
2
Актуализация знаний.
Цель – актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала:
Итак, составьте уравнение с двумя переменными по следующим условиям:
На верхней полке х книг, а на нижней у книг. Составьте уравнение с двумя переменными по следующему условию:
а) всего на полках 56 книг;
б) на верхней полке на 18 книг больше, чем на нижней;
в) на верхней полке на 27 книг меньше, чем на нижней;
г) после того, как с верхней полки сняли 6 книг, а на нижнюю поставили 8 книг, на полках стало книг поровну;
д) после того как с верхней полки переставили на нижнюю 10 книг, на полках стало книг поровну.
Выполняют задание.
Основная часть урока (операционная) (25 мин)
Изучение нового материала.
Цель – организовать коммуникативное взаимодействие для построения нового способа действия (алгоритма), устраняющего причину выявленного затруднения.
Задача 1. Высвечивается на экране. По тропинке вдоль кустов Шло одиннадцать хвостов. Сосчитать я также смог, что шагало 30 ног. Это вместе шли куда-то петухи и поросята. А теперь вопрос
таков: Сколько было петухов? И узнать я был бы рад сколько было поросят?
- Проблема: Как решить эту задачу?
- Что мы примем за х, что за у?
- Хорошо!
- прочитайте первое предложение задачи.
-какое уравнение с двумя переменными мы с вами можем составить.
- Читаем второе предложение и думаем: какое уравнение с двумя переменными мы с вами можем составить
- составим систему уравнений
- каким способом будем решать?
Пусть 1 ряд решает данную систему уравнений способом подстановки
2 ряд - способом сложения;
3 ряд - графически
Ответ: 7 петухов и 4 поросенка
Читают текст задачи.
Обсуждают.
Пусть поросят было х, тогда у было петухов.
х + у =11
4х + 2у = 30
Личностные: самоопределение, смыслообразование.
Регулятивные:волеваясаморегуляция в ситуации затруднения.
Познавательные: анализ, синтез, обобщение, аналогия, самостоятельное выделение и формулирование познавательной цели, поиск и выделение необходимой информации, проблема выбора эффективного способа решения, создание способа решения проблемы.
Коммуникативные: выражение своих мыслей, аргументирование своего мнения, учебное сотрудничество со сверстниками.
Закрепление. Формирование практических навыков решения задач.
Цель – организовать усвоение детьми нового способа действия решения заданий с их проговариванием во внешней речи.
- Выполним задания у доски и в тетрадях с пошаговым комментарием.
№ 14.7
- Прочитайте условие задачи. Перескажите.
- Составим модель задачи на доске и в тетради.
- Решим задачу с комментированием (по алгоритму).
Пусть х- первое число, у -второе число.
Утроенная разность этих чисел на 6 больше их суммы, т. е
3(х - у) - 6 = х + у.
Удвоенная разность этих чисел на 9 больше их суммы, т. е
2(х - у) -9 = х + у.
Составим и решим систему уравнений
Ответ: у = -6; х = 27
Мы рассмотрели 2 задачи, что общего вы увидели при решении этих задач?
Работа с учебником.
Один ученик составляет первое уравнение, второй ученик составляет второе уравнение. Третий -решает систему.
Этапы решения задач
1. Составление математической модели (система уравнений).
2. Работа с составленной моделью.
3. Ответ на вопрос задачи.
Личностные: осознание ответственности за общее дело
Познавательные:выполнение действий по алгоритму, построение логической цепи рассуждений, анализ, обобщение, подведение под понятие.
Коммуникативные: выражение своих мыслей, использование речевых средств для решения коммуникативных задач.
Самостоятельная работа. Самопроверка.
Цель – организовать самостоятельное выполнение учащимися типовых заданий на новый способ действия
Ребята, сейчас каждый проверит сам себя, насколько он сам научился решать задачи с помощью уравнения
Задача №2. Высвечивается на экране.
Фильтр от сигареты разлагается на 10 лет дольше, чем консервная банка. С созданием материалов, разлагающихся под воздействием света можно уменьшить период разложения фильтра в 2 раза, а консервной банки в 5 раз, тогда разница между периодами разложения будет 32 года. Найдите период разложения каждого предмета.
Самостоятельная работа в парах с промежуточной проверкой.
Математическая модель
- Как вы поняли из условия задачи, что на разложение различных веществ требуется определенное время, иногда несравнимо большее, чем человеческая жизнь. Проверьте свое решение, рассмотрите таблицу и выскажите свое соображение, что можно сделать с подобным мусором.
(результаты высвечиваются в таблице с другими данными на экране)
Периоды разложения некоторых веществ
Материал
Время разложения
Консервная банка
90 лет
Фильтр от сигареты
100 лет
Полиэтиленовый пакет
200 лет
Пластмасса
500 лет
Стекло
1000 лет
- Оцените себя.
Осуществляют самопроверку.
Проверяют свои ответы, исправляют допущенные ошибки. Осуществляют самооценку.
Регулятивные: контроль, коррекция, самооценка
Познавательные: анализ, синтез, аналогия, выполнение действий по алгоритму.
Домашнее задание.
Цель – обсудить и записать домашнее задание.
Домашнее задание.
- Запишите задание: Прочитать п.14 учебника.
Задача: Можно ли разменять купюру в 1000 рублей купюрами в 10 рублей и 50 рублей. если для размена можно использовать 26 купюр?
Записывают домашнее задание.
Итог урока (рефлексивно-оценочная) (5 мин)
Цель – организовать оценивание учащимися собственной деятельности на уроке.
- Удалось ли вам решить проблему урока?
- Какие знания, полученные ранее, позволили открыть новое?
- Проанализируйте свою работу.
- Что понравилось? Что, по-вашему, не удалось?
Называют основные позиции нового материала и как они их усвоили.
Познавательные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Коммуникативные: аргументация своего мнения