Конспект урока по теме "Обыкновенные и десятичные дроби"

Обыкновенные и десятичные дроби

Машичева Г.Н.

Урок обобщения и систематизации.

1. То, что ученик должен знать:

-алгоритмы сложения, вычитания, умножения и деления обыкновенных дробей и смешанных чисел,

-алгоритмы сложения, вычитания, умножения и деления десятичных дробей,

- нахождения неизвестного компонента при решении простейших уравнений,

-правила нахождения скорости движения объекта, времени и расстояния.

2) То, что ученик мог забыть (и надо повторить):

-применение переместительного и сочетательного свойств сложения и умножения,

-применение распределительного свойства умножения относительно сложения и вычитания применительно к буквенным выражениям,

- понятие взаимно обратных чисел,

1. Повторить и закрепить умения складывать и вычитать, умножать и делить обыкновенные дроби и смешанные числа.

2. Повторить и закрепить умения складывать, вычитать, умножать и делить десятичные дроби.

3. Повторить и закрепить умения решения простейших уравнений.

4. Повторить и закрепить умения решать задачи (в 2 действия, на движение).

5. Повторить и закрепить умение применять переместительное и сочетательное свойства сложения и умножения.

6) Повторить и закрепить умение применять распределительное свойство умножения для упрощения буквенных выражений.

7) Повторить и закрепить умения находить значение буквенного выражения при заданном значении переменной.

1. Организационный момент и устный счет (10 мин).

2. Актуализация знаний (3 мин).

3. Выполнение письменных заданий обобщающего и систематизирующего характера (23 мин).

4. Самостоятельная работа (8 мин).

5. Постановка домашнего задания (1 мин).

Читая замечательный роман английского писателя Даниеля Дефо «Приключения Робинзона Крузо», поколения ребят восхищаются мужеством героя романа, мечтают попасть на такой же необитаемый остров, испытать собственные силы, проверить характер. И мало кто знает, что этот роман основан на реальной истории и этот удивительный остров действительно существует. Один из группы островов архипелага Хуан Фернандес, расположенного в Тихом океане, назван в честь героя романа островом Робинзона Крузо. И сегодня мы с вами постараемся совершить заочное путешествие и достичь берегов необычного острова Робинзона, закрепить и обобщить знания по теме «Обыкновенные и десятичные дроби».

Запишите в тетради тему урока: Обыкновенные и десятичные дроби.

_{     }

? ? ?

_{     }

_{     }

? ? ?

Вам интересно узнать имя реального прототипа Робинзона Крузо? Тогда давайте устно решим примеры и расшифруем его имя. [Задания предъявляются по одному. Учитель организует работу со всем классом – дети считают друг за другом, по собственному желанию, а кто-то по вызову учителя. Учитель обращает внимание учащихся на то, что считают, показывая на эту запись указкой и делает записи на доске, записывая ответы в пробелах.]

Перед вами столбики примеров. Ответ первого примера является началом примера, который мы будем решать вторым. Вам необходимо, выполнить вычисления всех примеров столбика и назвать окончательный результат.

_{ }

?

Выполним первый пример, 1/3 плюс 1/5 . Какой будет результат?

8/15

Ответ первого примера, число 8/15, является начало второго, то есть слагаемым в примере 8/15 плюс 7/15. Чему будет равна сумма?

1

Объясните, как получили этот результат?

8/15 плюс 7/15 получим 15/15 или 1.

_{ }

1

Число 1 – окончательный результат. Запишем этот результат вместо знака вопроса.[Учитель стирает знак вопроса и записывает число 1.]

Откроем окошко соответствующее числу 1. [Учитель открывает окошки с буквой Е.]

_{ }

?

Вычислим, . Какой будет результат?

¼

Чему равен первый множитель во втором примере?

Запомним это число.

1/4

Что делаем дальше?

Находим произведение ¼ умножить на 8. Получим, 2.

_{ }

2

Окончательный ответ 2. Куда запишем этот результат? [Учитель стирает знак вопроса и записывает число 2. После этого появляется окончательная запись на доске.]

Вместо знака вопроса.

Откроем соответствующее окошко. [Учитель открывает окошко с буквой R.]

_{ }

?

Следующий столбик примеров.

Выполним первый пример. Какой будет результат?

3/5

Что делаем дальше?

Находим разность чисел 3/5 и 1/15.Получим, 8/15.

_{ }

8/15

Куда запишем окончательный результат? [Учитель стирает знак вопроса и записывает число 8/15. После этого появляется окончательная запись на доске.]

[Учитель открывает окошко с буквой S.]

Окончательный результат запишем вместо знака вопроса.

Откроем соответствующее окошко. [Учитель открывает окошко с буквой S.]

_{ }

_{ }

?

Попробуйте, не называя промежуточного ответа, ответа первого примера, назвать окончательный результат. [Если учащиеся затрудняются дать ответ, то учитель строит диалог дальше]

5/6

Выполним первый пример. Какой будет результат?

1/6

Что делаем дальше?

Находим сумму чисел 1/6 и 2/3. Получим, 5/6.

_{ }

_{ }

5/6

Куда запишем окончательный результат? [Учитель стирает знак вопроса и записывает число 5/6. После этого появляется окончательная запись на доске.]

[Учитель открывает окошки с КI.]

Окончательный результат запишем вместо знака вопроса.

Откроем соответствующие окошки. [Учитель открывает окошки с буквой К.]

_{ }

_{ }

?

Следующий столбик примеров.

Попробуйте, не называя промежуточного ответа, ответа первого примера, назвать окончательный результат. [Если учащиеся затрудняются дать ответ, то учитель строит диалог дальше]

1 1/7

Выполним первый пример. Какой будет результат?

2

Что делаем дальше?

Находим разность чисел 2 и 6/7. Разность равна 1 1/7.

_{ }

_{ }

1 1/7

Куда запишем окончательный результат? [Учитель стирает знак вопроса и записывает число 1 1/7. После этого появляется окончательная запись на доске.]

[Учитель открывает окошко с буквой L.]

Окончательный результат запишем вместо знака вопроса.

Откроем окошко. [Учитель открывает окошко с буквой L.]

_{ }

_{ }

?

Попробуйте, не называя промежуточного ответа, ответа первого примера, назвать окончательный результат. [Если учащиеся затрудняются дать ответ, то учитель строит диалог дальше]

15/56

Выполним первый пример. Какой будет результат?

1/8

_{ }

_{ }

15/56

Что делаем дальше?

Находим сумму чисел 1/8 и 1/7. Сумма равна 15/56.

Откроем окошко. [Учитель открывает окошко с буквой I.]

Александр Селкирк был матросом на судах английского военного флота.27-летний боцман судна «Сэнк пор» отправился к берегам Южной Америки. В мае 1704 г. корабль, повреждённый штормом, стал на якорь возле острова Мас-а-Тьера (ныне –Робинзона), где произошёл раздор между капитаном и Селкирком, в результате последнего высадили на безлюдный остров с небольшим запасом пороха и пуль. В мае 1704 г., из-за ссоры с капитаном, Селкирка высадили на безлюдный остров (ныне –остров Робинзона).

«Если меня что-то спасло, - говорил Селкирк позже,- так это труд». Прислушаемся к его мудрым словам и продолжим трудиться.

4+1/9+8/9 1/10*7/11*10

2/7+(1/14+5/7) 4/5*(5*1/2)

Продолжаем работать устно. Выполните вычисления в наиболее удобном порядке.

4+1/9+8/9

Какие числа в этом выражении удобно сложить? [Учитель обращает внимание учащихся на то, какой пример выполнять, показывая на эту запись указкой.]

1/9 и 8/9.

Почему?

Это дроби с одинаковыми знаменателями.

Верно. Перед нами выражение, содержащие только действия сложения, значит, складывать числа мы можем в любом порядке. Это позволяют нам делать переместительное и сочетательное свойства сложения.

[После ответа учеников на доске появляется буквенная запись этого свойства.]

Переместительное свойство

a+b=b+a

Давайте вспомним, эти свойства сложения. Сформулируйте переместительное свойство сложения.

[Учитель выдерживает паузу в несколько секунд, если учащиеся не могут вспомнить, то просит их посмотреть в копилку]

Если вам необходима помощь, чтобы ответить на вопрос, то посмотрите в копилку. [ Если учитель не получает правильного ответа, то сам дает верный ответ.]

От перестановки мест слагаемых сумма не изменяется.

Сочетательное свойство

a+(b+c)=(a+b)+c= a+b+c.

[Записи этих свойств остаются на доске до окончания выполнения этого задания.]

Сочетательное свойство сложения позволяет при наличии скобки изменить порядок сложения чисел [После слов учителя на доске появляется выражение =(a+b)+c .]

или просто скобки опустить. [После слов учителя на доске появляется выражение = a+b+c.]

4+1/9+8/9

Вернемся к нашему заданию и продолжим выполнять вычисления. [Учитель обращает внимание учащихся на то, какой пример выполнять, показывая на эту запись указкой.]

Сложим 1/9 и 8/9.

Сколько получится?

Получится 1.

Что осталось сделать?

Сложить 1 и 4.

4+1/9+8/9=5

Что получится в результате? [Учитель записывает на доске число 5.]

Получится 5.

2/7+(1/14+5/7)= 2/7+1/14+5/7[После ответа учеников на доске появляется запись без скобок.]

Следующее выражение. Здесь также только действие сложение, но есть скобки. Что мы можем сделать?

Мы можем опустить скобки.

[После ответа учеников числа 2/7 и 5/7или выделить другим цветом или подчеркнуть.]

Верно, сочетательное свойство сложения позволяет нам опустить скобки. Какие два числа удобно сложить первыми?

2/7 и 5/7

Почему?

Это дроби с одинаковыми знаменателями.

Сколько получится?

Получится 1.

Менять слагаемые местами нам позволяет переместительное свойство, но мы новое выражение не записываем, так как слагаемых мало, и мы можем представить себе это выражение «в уме».

Что осталось сделать?

Сложить 1 и 1/14.

2/7+(1/14+5/7)= 2/7+1/14+5/7=1 1/14

Что получится в результате? [Учитель записывает на доске число 1 1/14.]

Получится 1 1/14.

1/10*7/11*10[После ответа учеников числа 1/10 и 10 или выделить другим цветом или подчеркнуть.]

Следующее выражение. [Учитель обращает внимание учащихся на то, какое пример выполнять, показывая на эту запись указкой.]

Какие числа в этом выражении удобно перемножить?

1/10 и 10

Чему равно произведение этих чисел?

1

Верно. Перед нами выражение, содержащие только действия умножения, значит, умножать числа мы можем в любом порядке. Это позволяют нам делать переместительное и сочетательное свойства умножения.

[После ответа учеников на доске появляется буквенная запись этого свойства.]

Переместительное свойство

а*b=b*a

Давайте вспомним, эти свойства умножения. Сформулируйте переместительное свойство умножения.

[Учитель выдерживает паузу в несколько секунд, если учащиеся не могут вспомнить, то просит их посмотреть в копилку]

Если вам необходима помощь, чтобы ответить на вопрос, то посмотрите в копилку. [ Если учитель не получает правильного ответа, то сам дает верный ответ.]

От перестановки мест сомножителей произведение не изменяется.

Сочетательное свойство

а*(b*c)=(a*b)*c= a*b*c.

[Записи этих свойств остаются на доске до окончания выполнения этого задания.]

Сочетательное свойство умножения позволяет при наличии скобки изменить порядок умножения чисел [После слов учителя на доске появляется выражение =(a*b)*c .]или просто скобки опустить. [После слов учителя на доске появляется выражение =a*b*c .]

1/10*7/11*10

Итак, мы умножили числа 1/10 и 10, получилось 1. [Учитель обращает внимание учащихся на то, какой пример выполнять, показывая на эту запись указкой.]

Что осталось сделать?

Перемножить 1 и 7/11.

1/10*7/11*10=7/11

Что получится в результате? [Учитель записывает на доске число 7/11.]

Получится 7/11.

4/5*(5*1/2) =4/5*5*1/2[После ответа учеников на доске появляется запись без скобок.]

И последнее выражение. Здесь также только действие умножения, но есть скобки. Что можно сделать?

Можно опустить скобки.

Верно, сочетательное свойство умножения позволяет нам опустить скобки и перемножить вначале удобные числа. Что делаем теперь?

Умножим 4/5 на 5, получим 4.

Что осталось сделать?

Умножить 4 на ½.

4/5*(5*1/2) =4/5*5*1/2=2

Что получится в результате? [Учитель записывает на доске число 2.]

2.

Вы слышите голос стихии, голос моря? Оно сурово и не прощает ошибок. Оно шлет испытания, которые выдерживают только смелые и знающие моряки. Давайте проверим, готовы ли мы отправиться в столь отчаянное плаванье к острову Робинзона, на котором Селкирк провёл почти 5 лет, и выполним следующее задание.

Среди записанных чисел выберите:

- обыкновенные дроби;

- натуральные числа;

-смешанные числа;

- десятичные дроби:

3/7; 0,7; 1 4/7; 7.

[Учитель организует обсуждение со всем классом, вызывая учащихся и учитывая их желание ответить, делает записи на доске.]

Обыкновенные дроби: 3/7.

Выберите обыкновенные дроби.

3/7

Натуральные числа: 7.

Среди записанных чисел выберите натуральные.

7.

Смешанные числа: 1 4/7.

Выберите смешанные числа.

1 4/7.

Десятичные дроби: 0,7.

Выберите десятичные дроби.

0,7.

[Учитель организует обсуждение со всем классом, вызывая учащихся и учитывая их желание ответить, делает записи на доске, остальные выполняют в тетради, записи в тетради появляются такие же, как на доске.]

Давайте вспомним, какие числа называются взаимно обратными числами?

[Учитель выдерживает паузу в несколько секунд, если учащиеся не могут вспомнить, то просит их посмотреть в копилку]

Если вам необходима помощь, чтобы ответить на вопрос, то посмотрите в копилку. [ Если учитель не получает правильного ответа, то сам дает верный ответ.]

Два числа, произведение которых равно 1, называют взаимно обратными.

Назовите число, обратное числу 3/7.

7/3

Выделите целую часть.

2 1/3

Взаимно обратные числа: 3/7 и 2 1/3;

Значит, число 2 1/3 обратно числу 3/7.

Взаимно обратные числа: 3/7 и 2 1/3;

Взаимно обратные числа: 3/7 и 2 1/3; 7 и 1/7;

Назовите число, обратное числу 7.

1/7

Взаимно обратные числа: 3/7 и 2 1/3; 7 и 1/7;

Объясните, как вы его нашли.

Чтобы записать число, обратное к числу 7, надо записать дробь, в числителе которой 1, а в знаменателе данное число 7.

Взаимно обратные числа: 3/7 и 2 1/3;; 7 и 1/7; 1 4/7 и 7/11;

Назовите число, обратное числу 1 4/7. [Если учитель не получает правильного ответа, то строит диалог следующим образом.]

7/11

Взаимно обратные числа: 3/7 и 2 1/3;; 7 и 1/7; 1 4/7 и 7/11;

Рассмотрим число 1 4/7. С чего надо начать, чтобы найти число, обратное данному?

Представить смешанное число в виде неправильной дроби. Получим 11/7.

Что будем делать дальше?

Найдем число, обратное дроби 11/7. Это число 7/11.

Назовите число, обратное числу 0,7. [Если учитель не получает правильного ответа, то строит диалог следующим образом.]

1 3/7

Рассмотрим число 0,7. С чего надо начать, чтобы найти число, обратное данному?

Представить его в виде обыкновенной дроби 7/10.

Взаимно обратные числа: 3/7 и 2 1/3; 7 и 1/7; 1 4/7 и 7/11; 0,7 и 1 3/7;

Что будем делать дальше?

Найдем число, обратное дроби 7/10. Это число 10/7. Выделим целую часть. Получим, 1 3/7.

Взаимно обратные числа: 3/7 и 2 1/3; 7 и 1/7; 1 4/7 и 7/11; 0,7 и 1 3/7;

Вы отлично справились с заданием, а теперь, юные искатели приключений, в путь! Он будет не прост, но я надеюсь, что вы знаете, что в опасных странствиях дороже золота ценятся знания, умения и дружба.

Вычислите:

(2 1/16-2 ¾ ÷11)*1 3/29.

2 1 3

(2 1/16-2 ¾ ÷11)*1 3/29.

Вычислите.

[Учитель вызывает одного ученика к доске, остальные выполняют в тетради, записи в тетради появляются такие же, как на доске.]

Что делаем в первую очередь?

Расставим порядок действий.

Первое действие деление. Второе – вычитание. Третье – умножение.

2 1 3

(2 1/16-2 ¾ ÷11)*1 3/29.

1) 2 ¾ ÷11

Какое действие выполним первым?

Разделим 2 ¾ на 11.

1) 2 ¾ ÷11

2 ¾ ÷11= 11/4÷11

Чтобы разделить смешанное число на натуральное число, с чего надо начать?

Представить смешанное число в виде неправильной дроби: 2 ¾=11/4.

2 ¾ ÷11= 11/4÷11

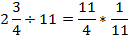Что теперь надо сделать?

Умножить 11/4 на число обратное 11, то есть 1/11.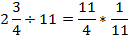

1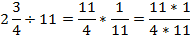

1

Какой следующий шаг?

Сократим на 11 полученную дробь.

1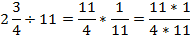

1

1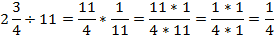

1

Что получим?

1/4

1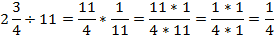

1

2) 2 1/16-1/4

Какое действие выполняем вторым?

Из числа 2 1/16 вычтем результат первого действия, дробь 1/4.

2) 2 1/16-1/4

Прокомментируйте, как это сделать.

Приводим дробную часть смешанного числа 2 1/16 и дробь 1/4 к наименьшему общему знаменателю. Общий знаменатель 16. Дополнительный множитель для дроби 1/4 равен 4. Получим, 2 1/16 минус 4/16.

1+1

1+1 1/16

Что делаем теперь?

Превратим дробную часть уменьшаемого в неправильную дробь, уменьшив на единицу целую часть. Получим, 1 17/16 минус 4/16.

1+1

1+1 1/16

Что получаем в результате второго действия?

Результат второго действия 1 13/16.

3) 1 13/16*1 3/29

Какое действие выполним третьим?

Результат второго действия, число 1 13/16, умножим на число 1 3/29.

3) 1 13/16*1 3/29

1 2

1 1

Самостоятельно выполните умножение. [Вычисление выполняется на закрытой доске. Затем решение открывается, и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

Какой получили результат?

2

1 2

1 1

2 1 3

(2 1/16-2 ¾ ÷11)*1 3/29=2.

Верно. Значение числового выражения равно 2. Запишем его в исходный пример.

2 1 3

(2 1/16-2 ¾ ÷11)*1 3/29=2.

Упростите выражения:

а) 2,308+а+0,09;

б) с+25,068+4,04;

в) в*79,6*0,01;

г) 42,7*х*0,08.

Первые дни нашего плавания прошли наредкость удачно, но внезапно разбушевалась стихия, несколько дней свирепствовали юго- западные ветра и океан швырял нас из стороны в сторону и так потрепал корабли, что требуется срочный ремонт. Нам необходимо выполнить расчеты, найти течь и заделать ее. Приступаем к выполнению задания: Упростите выражения.

Обратите внимание на выражения. Они содержат только действия сложения или умножения. Значит, можно применить свойства сложения и умножения. Они позволят нам менять слагаемые или множители местами, объединять числа по-разному. [Учитель вызывает одного за другим учеников к доске, остальные выполняют в тетради, записи в тетради появляются такие же, как на доске.]

а) 2,308+а+0,09

Упростим выражение. [Учитель обращает внимание учащихся на то, какой пример выполнять, показывая на эту запись указкой.]

Выражение содержит три слагаемых. Какие слагаемые мы можем сложить?

2,308 и 0,09

а) 2,308+а+0,09

2,308

+0,090

2,398

Сложите. Что получим? [Ученик выполняет вычисления на закрытой доске. Решение открывается и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

2,398

2,308

+0,090

2,398

Что делаем дальше?

Прибавим а.

а) 2,308+а+0,09=2,398+а.

Какое выражение получим?

2,398+а.

а) 2,308+а+0,09=2,398+а.

б) с+25,068+4,04=29,108+с

25,068

+ 4,040

29,108

Следующее выражение упростите самостоятельно. [Решение открывается и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

Какое выражение получим?

29,108+с

б) с+25,068+4,04=29,108+с

25,068

+ 4,040

29,108

в) в*79,6*0,01

Следующее выражение. Выражение содержит три множителя. Какие мы можем перемножить?

79,6 и 0,01

в) в*79,6*0,01

79,6

0,01

0,796

Выполните умножение. Что получим? [Решение открывается и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

0,796

79,6

0,01

0,796

в) в*79,6*0,01=0,796*в

Какое выражение получим?

0,796*в

в) в*79,6*0,01=0,796*в

в) в*79,6*0,01=0,796*в=0,796в

Знак умножения между числом и в можно опустить.

в) в*79,6*0,01=0,796*в=0,796в

г) 42,7*х*0,08=3,416*х=3,416х.

42,7

0,08

3,416

Следующее выражение упростите самостоятельно. [Решение открывается и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

Какое выражение получим?

3,416х

г) 42,7*х*0,08=3,416*х=3,416х.

42,7

0,08

3,416

Верно.

Мы потратили много сил на ремон кораблей, но теперь мы можем продолжить наше плаванье. Незаметно мы приближаемся к острову Робинзона, да вот беда, на горизонте внезапно появляются пиратские корабли, а это значит-неизбежна перестрелка.

Упростите выражение и найдите его значение:

а) k+k+k при k=2,3;

б) 4,2p-p+3,6 при p=0,2;

в) 8,8c +0,1+1,2с при с=0,19. [Выделенное зеленым выражение предъявляется, если останется время для его выполнения.]

Готовы к бою?

Упростим выражение. [Учитель вызывает одного за другим учеников к доске, остальные выполняют в тетради, записи в тетради появляются такие же, как на доске.]

а) k+k+k=1к+1к+1к

Как представить k в виде произведения числа и буквы?

1 умножить на к.

а) k+k+k=1к+1к+1к

Что будем делать, чтобы упростить выражение?

Найдем сумму чисел 1; 1 и 1 и умножим на общую буквенную часть к.

k+k+k=1к+1к+1к=3к

Что получим?

3к

k+k+k=1к+1к+1к=3к

Если к=2,3, то 3к=3*2,3=

Мы упростили выражение. Как найти его значение при к=2,3?

Заменим букву к ее значением 2,3.

Если к=2,3, то 3к=3*2,3=

Какое числовое выражение получили?

3 умножить на 2,3.

Если к=2,3, то 3к=3*2,3=6,9

Найдем значение получившегося числового выражения. Что получим?

6,9

Если к=2,3, то 3к=3*2,3=6,9

Наши расчеты оказались точны, залп бортовых орудий и один из кораблей пиратов потоплен.

б) 4,2p-p+0,36

На прицеле следующий корабль пиратов. Наши вычисления должны быть точны, промахнуться нельзя. Сначала упростим выражение.

б) 4,2p-p+0,36

4,2p-p+0,36 =

Подчеркните выражения с одинаковой буквенной частью.

Подчеркнем 4,2р и р.

4,2p-p+0,36 =

Как представим р?

1 умножить на р.

Выражения 4,2р и 1р содержат одинаковую буквенную часть, значит, мы можем найти их разность.

Как это сделать?

Найдем разность чисел 4,2 и 1 и умножим ее на р.

4,2p-p+0,36 =3,2р

Что получим?

3,2р

4,2p-p+0,36 =3,2р

Что делаем дальше?

Прибавим 0,36.

4,2p-p+0,36 =3,2р +0,36

Какое выражение получим?

3,2р+0,36

4,2p-p+0,36 =3,2р +0,36

Посмотрите на выражение, которое мы получили. Можно ли его упростить?

Нет.

Если р=0,2, то 3,2р+0,36=3,2*0,2+0,36=

Мы упростили выражение. Что делаем дальше?

Подставим вместо р число 0,2.

Если р=0,2, то 3,2р+0,36=3,2*0,2+0,36=

Какое числовое выражение получили?

3,2*0,2+0,36

Если р=0,2, то

1 2

3,2р+0,36=3,2*0,2+0,36=1

1) 3,2*0,2=0,64

2) 0,64

+0,36

1,00

Самостоятельно найдите значение получившегося числового выражения. [Ученик работает на закрытой доске, затем решение открывается и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

Какой получили результат?

1

Если р=0,2, то

1 2

3,2р+0,36=3,2*0,2+0,36=1

1) 3,2*0,2=0,64

3,2

0,2

0,64

2) 0,64

+0,36

1,00

И еще одно точное поражение вражеского корабля.

в) 8,8c +0,1+1,2с.

Следующее задание. Что сделаем в первую очередь?

Упростим выражение.

в) 8,8c +0,1+1,2с.

8,8c +0,1+1,2с.

1

8,8

+ 1,2

10,0

Что для этого надо сделать?

Найти сумму выражений 8,8с и 1,2с.

8,8c +0,1+1,2с.

1

8,8

+ 1,2

10,0

Найдите. Что получим?

10с.

Объясните, как вы нашли.

Нашли сумму чисел 8,8 и 1,2 и умножили ее на с.

8,8c +0,1+1,2с=10с+0,1.

Какое выражение получим?

10с+0,1

8,8c +0,1+1,2с=10с+0,1.

Что делаем дальше?

Подставим вместо с число 0,19.

Если с=0,19, то 10с+0,1=10*0,19+0,1

Какое числовое выражение получили?

10*0,19+0,1

Если с=0,19, то 10с+0,1=10*0,19+0,1

Если с=0,19, то

1 2

10с+0,1=10*0,19+0,1=2

1) 10*0,19=1,9

2) 1,9+0,1=2

Самостоятельно найдите значение получившегося числового выражения. [Ученик работает на закрытой доске, затем решение открывается и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

Какой получили результат?

2

Если с=0,19, то

1 2

10с+0,1=10*0,19+0,1=2

1) 10*0,19=1,9

2) 1,9+0,1=2

И следующий выстрел попадает точно в цель - флагманский корабль эскадры пиратов выведен из боя. Пиратам приходится спасаться бегством.

1) х- 1 2/5=5 ½ DА

2)12 4/5х=4 PI

3) х÷2 2/3=2 2/3 M

4) 3 1/6=2 1/3+х ER

По воле случая, своим спасением герой нашего путешествия Александр Селкирк обязан именно пирату. Хотите узнать имя этого великодушного пирата? Решив уравнения, мы его узнаем.

[Учитель организует фронтальную работу со всеми учащимися класса.]

1) х- 1 2/5=5 ½

2)12 4/5х=4

3) х÷2 2/3=2 2/3

4) 3 1/6=2 1/3+х

Среди выписанных уравнений, найдите уравнение с неизвестным множителем.

Второе уравнение – уравнение с неизвестным множителем.

Как вы это определили?

Знак умножения можно опускать, и он опущен между 12 4/5 и х.

2)12 4/5х=4

Х=4÷12 4/5

Х=5/16

2 1

32 16

Ответ: 5/16

Самостоятельно решите второе уравнение.

[Готовое решение открывается и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

Чтобы найти х, что надо сделать?

4 разделить на 12 4/5

2)12 4/5х=4

Х=4÷12 4/5

Х=5/16

2 1

32 16

Ответ: 5/16

Почему?

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Какой получили результат?

5/16

Такое число есть в таблице?

Есть.

Запишем в таблицу под числом 5/16 соответствующие буквы. [Учитель выписывает буквы на доске.]

1) х- 1 2/5=5 ½

2)12 4/5х=4

3) х÷2 2/3=2 2/3

4) 3 1/6=2 1/3+х

Среди выписанных уравнений, найдите уравнение с неизвестным слагаемым.

Четвертое уравнение – уравнение с неизвестным слагаемым.

Что можно сделать с левой и правой частями уравнения?

Левую и правую части уравнения можно поменять местами.

4) 3 1/6=2 1/3+х

2 1/3+х=3 1/6

Х=3 1/6-2 1/3

Х=5/6

Ответ: 5/6

Самостоятельно решите четвертое уравнение.

[Готовое решение открывается и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

Чтобы найти х, что надо сделать?

Из 3 1/6 вычесть 2 1/3

4) 3 1/6=2 1/3+х

2 1/3+х=3 1/6

Х=3 1/6-2 1/3

Х=5/6

Ответ: 5/6

Почему?

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

Какой получили результат?

5/6

Заполним соответствующее окошко в таблице.

За годы, проведенные на необитаемом острове, Александр Селкирк совсем забыл математику. Пытаясь решить уравнения, он допустил ошибки. Давайте их найдем и исправим.

1) х- 1 2/5=5 ½

Х=5 1/2-1 2/5

Х=4 1/10

Какая ошибка допущена при решении первого уравнения?

Чтобы найти х, надо к 5 ½ прибавить 1 2/5

Почему?

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

[Если учитель не получает правильного ответа, то строит диалог следующим образом.]

Какой компонент неизвестен?

Уменьшаемое

Как найти неизвестное уменьшаемое?

Надо к разности прибавить вычитаемое.

Чтобы найти х, что надо сделать?

К 5 ½ прибавить 1 2/5.

Верно ли решено уравнение?

Неверно.

1) х- 1 2/5=5 ½

Х=5 1/2+1 2/5

Х=6 9/10

Ответ: 6 9/10

Выполните вычисления и исправьте ошибку. [Готовое решение открывается и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

Какой получили результат?

6 9/10

1) х- 1 2/5=5 ½

Х=5 1/2+1 2/5

Х=6 9/10

Ответ: 6 9/10

Заполним соответствующее окошко в таблице.

3) х÷2 2/3=2 2/3

Х=2 2/3÷2 2/3

Х=1

Какая ошибка допущена при решении третьего уравнения?

Чтобы найти х, надо 2 2/3 умножить на 2 2/3.

Почему?

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

[Если учитель не получает правильного ответа, то строит диалог следующим образом.]

Какой компонент неизвестен?

Делимое

Как найти неизвестное делимое?

Надо частное умножить на делитель.

Чтобы найти х, что надо сделать?

2 2/3 умножить на 2 2/3.

Верно ли решено уравнение?

Неверно.

3) х÷2 2/3=2 2/3

Х=2 2/3*2 2/3

Х=21 1/3

64|9

-63 7

1(ост)

Ответ: 7 1/9

Выполните вычисления и решите верно это уравнение. [Готовое решение открывается и учитель просит учеников проверить, как они выполнили задание, исправить ошибки.]

Какой получили результат?

7 1/9

3) х÷2 2/3=2 2/3

Х=2 2/3*2 2/3

Х=21 1/3

64|9

-63 7

1(ост)

Ответ: 7 1/9

Заполним таблицу.

2 февраля 1709 г. военный английский корабль флотилии Уильяма Дампьера «Duke» обнаружил на острове человека, им оказался Александр Селькирк. Матрос провёл на острове почти 5 лет

Мы достигли цели нашего путешествия, перед нами остров Робинзона Крузо. Остров Робинзона Крузо чрезвычайно живописен – на нем много лесов. В лесах множество редких растений, которые не растут больше нигде, и экзотических птиц. До сих пор в некоторых уголках острова можно встретить знаменитых одичавших коз, описанных в романе.

Александр Селькирк, охотясь на коз, бежит со скоростью 20,8 км/ч и преодолевает расстояние от шалаша до смотровой площадки за 1,2 ч. С какой скоростью двигается стадо коз, если они преодолевают это же расстояние за 0,6 ч?

Немало труда, выдумки и изобретательности потребовалось Александру Селькирку для того, чтобы наладить жизнь на необитаемом острове. Подобно первобытным людям, он научился добывать огонь 
трением, а когда у него кончился порох - стал ловить руками диких коз. Умение быстро бегать - один из многих полезных навыков, в которых он преуспел за время жизни на острове, тренируясь вместе с козами.

Александр Селькирк, охотясь на коз, бежит со скоростью 20,8 км/ч и преодолевает расстояние от шалаша до смотровой площадки за 1,2 ч. С какой скоростью двигается стадо коз, если они преодолевают это же расстояние за 0,6 ч?

Решим задачу, по действиям, не составляя пропорцию. [Учитель вызывает одного ученика к доске, остальные выполняют в тетради, записи в тетради появляются такие же, как на доске.]

Это задача на движение. Какими величинами характеризуется движение?

Скорость, время, расстояние.

Км/ч ч км

В первой строке схемы запишем названия величин: скорость в км/ч, время в ч, расстояние в км.

Км/ч ч км

Селькирк

Козы

О каких объектах идет речь в задаче?

В задаче идет речь о Селькирке и козах.

Км/ч ч км

Селькирк 20,8 1,2 ?

Козы ? 40 0,6 ?

Уточните известные и неизвестные величины.

Известны скорость Селькирка 20,8 км/ч, время его движения 1,2 ч и время движения коз 0,6 ч. Неизвестно расстояние, пройденное каждым объектом и скорость движения коз.

Какая связь существует в задаче между расстоянием, которое пробежал Селькирк и расстоянием, которое преодолели козы?

Расстояние, преодоленное Селькирком и козами одинаково.

Км/ч ч км

Селькирк 20,8 1,2 ? одинаково

Козы ? 0,6 ?

Где в условии это отмечено? [Учитель в условии на доске выделяет( подчеркивает) словосочетание «они преодолевают это же расстояние».]

С какой скоростью двигается стадо коз, если они преодолевают это же расстояние за 0,6 ч?

Км/ч ч км

Селькирк 20,8 1,2 ? одинаково

Козы ? 0,6 ?

Что требуется найти?

С какой скоростью двигается стадо коз.

Что нужно знать, чтобы узнать, с какой скоростью двигается стадо коз ?

Расстояние и время.

Что мы знаем?

Время – 0,6 ч.

Что надо узнать?

Расстояние, преодоленное козами.

Чему оно равно?

Расстоянию, преодоленному Селькирком.

1) 20,8*1,2=24,96(км) – пробежал Селькирк.

20,8

1,2

416

+208

24,96

Как найти расстояние, которое пробежал Селькирк?

Надо скорость 20,8 км/ч умножить на время 1,2 ч.

1) 20,8*1,2=24,96(км) – пробежал Селькирк.

20,8

1,2

416

+208

24,96

Что теперь можно узнать?

С какой скоростью двигается стадо коз.

2) 24,96÷0,6=41,6(км/ч)-скорость движения коз.

249,6|6

-24 41,6

9

-6

36

-36

0

Как узнать скорость?

Надо расстояние 24,96 км разделить на время, за которое козы преодолевают это расстояние 06 ч.

2) 24,96÷0,6=41,6(км/ч)-скорость движения коз.

249,6|6

-24 41,6

9

-6

36

-36

0

Мы ответили на вопрос задачи?

Да.

Ответ: 41,6 км/ч

С какой скоростью двигалось стадо коз? Запишите ответ.

41,6 км/ч.

Ответ: 41,6 км/ч

[Карточки с дополнительными заданиями для сильных учащихся.]

Карточка №1.

В коробке лежали карандаши. Сестра взяла половину всех карандашей и еще полкарандаша. Остальные 4 карандаша взял брат. Сколько карандашей было в коробке первоначально?

[Учащиеся работают в карточках. Карточки сдаются учителю на проверку. Учащимся предъявляется готовый вариант решений на карточках, для работы дома.]

Сестра взяла половину всех карандашей (на рисунке – красного цвета) и еще полкарандаша из второй половины.

Брат взял 4 остальных карандаша ( на рисунке – синего цвета).

Значит, 4 карандаша, которые взял брат и полкарандаша (синего цвета), которые взяла сестра – это половина всех карандашей.

1) 4+1/2=4 ½(карандашей)-половина всех карандашей.

2) 4 1/2*2=9/2*2= (карандашей)-в коробке.

Ответ: 9 карандашей.

[Карточки с дополнительными заданиями для сильных учащихся.]

Карточка №2.

Лифт от 1-го до 2-го этажа идет 4 с. Сколько секунд он будет идти без остановки от 1-го до 6-го этажа?

6

5

4

3

2

1

От 1-го этажа до 2-го один пролет.

А от 1-го до 6-го этажа 5 таких пролетов.

4*5=20(с) - идет лифт до 6-го этажа.

Ответ: 20 с.

Оставляю вас на острове полюбоваться его природой, пофантазировать, представить себе жизнь одинокого скитальца. Справились бы вы с теми испытаниями, которые выпали на долю отшельника? Обладаете ли вы необходимыми для этого знаниями? Давайте проверим, хорошо ли вы запомнили все что увидели и услышали сегодня на уроке.

1) Решите уравнения:

а) х÷1 3/25=7 ½;

б) 7 3/7-у=4 8/21;

в) 4 2/3÷а=2/9.

а) х÷1 3/25=7 ½

х=7 ½*1 3/25

х=8 2/5

3 14

1 5

42|5

-40 8

2(ост)

Ответ: 8 2/5

б) 7 3/7-у=4 8/21

у=7 3/7-4 8/21

у=3 1/21

Ответ: 3 1/21

в) 4 2/3÷а=2/9

а=4 2/3÷2/9

а=21

7 3

1 1

Ответ: 21

2) Упростите выражение и найдите его значение:

6,3с-3,75с-2,9 при с=40.

[Критерии оценок:

«5» за все 2 верно выполненных задания,

«4» если допущены 1-2 ошибки,

«3» если выполнено верно1 задание,

«2» если верно выполнено менее 1 задания.]

6,3с-3,75с-2,9=2,55с-2,9

• •

6,30

-3,75

2,55

1 2

Если с=40, то 2,55*40-2,9=99,1

1) 2,55

40

102,00

• 9 •

2) 102,0

- 2,9

99,1

Выполните действия:

4 1/3 –(8 7/60+3 ¾-8 7/15)

[Тетради сдаются учителю на проверку.]

3 1 2

4 –(5 7/60+3 ¾-8 7/15)=3 2/3

26 13

1) _{ }

30 15

1

2) 

 3

3) _{ }

Упростите выражение и найдите его значение:

а) 0,4х+1,1х+0,3х при х=100;

б) у*2,5*40 при у=0,003;

в) 49+а+0,7 при а=1,3.

а) 0,4х+1,1х+0,3х=1,8х

Если х=100, то 1,8*100=180;

б) у*2,5*40=у*100

2,5

40

100,0

Если у=0,003, то 0,003*100=0,3;

в) 49+а+0,7=49,7+а

Если а=1,3, то 49,7+1,3=51

49,7

+ 1,3

51,0

Самая маленькая в мире птица калибри развивает в полете скорость 81 км/ч, а зеленокрылый ара летит со скоростью 48,6 км/ч. Сколько времени необходимо попугаю, чтобы пролететь расстояние, которое преодолевает калибри за 0,3 ч?

Км/ч ч км

Калибри 81 0,3 ? одинаково

Попугай 48,6 ? ?

1) 81*0,3=24,3(км)-пролетела калибри.

81

0,3

24,3

2) 24,3÷48,6=0,5(ч)-летит попугай.

243,0|486

- 2430 0,5

0

Ответ: 0,5 ч.