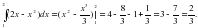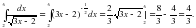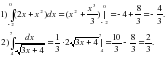«Интеграл»
(Открытый урок в 11 классе)
Цели урока: 1. Повторить понятие и закрепить умение вычислять интегралы.
2. Продолжить формирование логического мышления.
.
Ход урока.
I. Проверка домашнего задания.
Вычислить интегралы:
1)
2)
3)
II. Устная работа.
а) Фронтальный опрос:
1) Дать определение первообразной функции f(x).
2) Что называется интегрированием?
3) Дать определение криволинейной трапеции.
4) Что называют интегралом функции f(x)?
5) В чем заключается геометрический смысл интеграла?
б) Найти одну из первообразных функции:
-5х+2; Cos ;
х2-5х4; Sin(1,5х+2)+2
(2х+5)5; Cos2 -Sin2 .
в) Вычислить интеграл:
; .
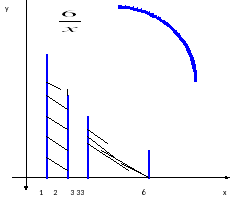
III. Докажите, что площади криволинейных трапеций, заштрихованных на рисунке, равны.
S1=
S2=
IV. Вычислить интеграл:
1)
=
2)
3)
4) Дополнительно для сильных учащихся.
По заданной площади криволинейной трапеции найдите значение параметра а:
(0<а< ).
Преобразуем подынтегральную функцию:
По условию -2Cos ( )+1=2,
Cos( )=- ,
Проведем отбор корней:
Если п=0, а= . Других решений, принадлежащих промежутку (0; ) нет.
Ответ: а= .
V. Самостоятельная работа.
I вариант.
1)
2)
II вариант.
VI. Домашнее задание:
1) № 581
2) Построить графики двух функций на одной координатной плоскости:
у=х2, у=х+3
VII. Итоги урока.
;
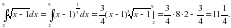
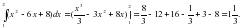
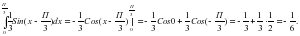
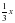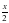-Sin2
; 
.
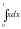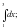
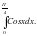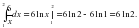
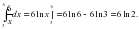
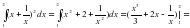
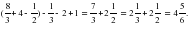
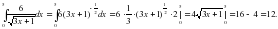
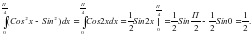
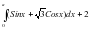(0а).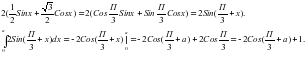
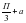)+1=2,
,
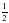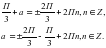
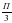. Других решений, принадлежащих промежутку (0;
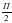) нет.
