П?н предмет Алгебра сынып класс 8
Та?ырыбы тема : Формула корней квадратного уравнения
Ма?саты цель:
- Формирование умения решать квадратное уравнение с помощью формулы; определять количество корней квадратного уравнения в зависимости от знака дискриминанта.
- Развитие способностей опознавать, анализировать, сопоставлять факты, делать выводы.
- Воспитание активности, умения общаться и сотрудничать.
Саба? турі Тип урока: изучение нового материала.
Вид урока: урок с применением ИКТ.
Оборудование:
- компьютер;
- проектор;
- презентация,
- раздаточный материал
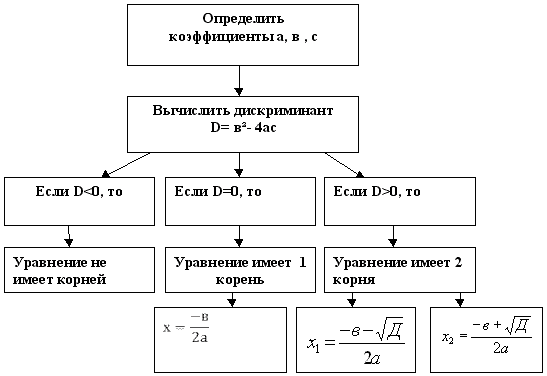
- "Алгоритм решения квадратного уравнения"
Формы работы учащихся на уроке: индивидуальная, фронтальная.
Структура урока:
1. Организационный момент
2. Устная работа
3. Изучение нового материала
4. Первичное закрепление материала
5. Странички истории
6. Самостоятельная работа
7. Домашнее задание
8. Итог урока
Саба? барасы Ход урока
1. Вступительное слово учителя
Ребята! Сегодня тема урока: "Формула корней квадратного уравнения". (Записывается тема урока, слайд 1) Эпиграфом нашего урока служат слова двух великих математиков:
"Приобретать знания - это храбрость.
Приумножать знания - это мудрость.
А умело применять - великое искусство"(слайд 2)
II.Устная работа
А)Ответьте на вопросы:
1. Какое уравнение называется квадратным?
2. Какое квадратное уравнение называется неполным?
3. Какое квадратное уравнение называется приведенным?
4. Что значит решить квадратное уравнение?
5. Сколько корней может иметь квадратное уравнение?
Б)1. Назовите вид данного уравнения.(слайд7)
2. Назовите его коэффициенты.
(22, 12, 2010)
Цифровой диктант
На доске задания:
Задание №1
Выпишите под какими номерами
стоят квадратные уравнения?
Задание №2
Дайте характеристику каждого квадратного уравнения.
Задание №3
Сколько корней имеет уравнение 4), 6), 7), 9)?
3 Проверка д/з № 118 сличение с доской
4. Рассмотрим, как можно иначе решить данное уравнение.
Сущестует формула для нахождения корней квадратного уравнения , т.е когда мы с вами рассматривали тему «Выделение квадрата двучлена», мы выделили квадратный дучлен
-b ± √D
x = ————, где D = b2 – 4ac.
2а
Латинской буквой D обозначают дискриминант.
Дискриминант - это выражение, от которого зависит число корней данного уравнения.
Для этого мы просмотрим решение нескольких квадратных уравнений
Пример.
Пример 1
Решите уравнение x 2 + 2 x – 3 = 0.
а=1, в=2, с = -3
Показать решение
Вычислим дискриминант этого уравнения: Следовательно, по формуле корней квадратного уравнения можно сразу получить, что Значит,
Ответ. 1, −3.
Пример 2
Решите уравнение x 2 + 6 x + 9 = 0.
Показать решение
Вычисляя дискриминант этого уравнения, получим, что D = 0 и, следовательно, это уравнение имеет один корень Однако можно поступить проще, заметив, что в левой части данного уравнения стоит полный квадрат: Отсюда равенство x = –3 получается сразу.
Ответ. x = –3.
Пример 3
Решите уравнение x 2 + 2 x + 17 = 0.
Показать решение
Вычислим дискриминант этого уравнения: D = 2 2 – 4 · 17 = –64 < 0. Следовательно, данное уравнение действительных корней не имеет.
Ответ. Решений нет.
Вывод:
Если D < 0, то уравнение не имеет корней.
Если D = 0, то уравнение имеет один корень.
Если D > 0, то уравнение имеет два корня.
Пример. Решим уравнение 12x2 + 7x + 1 = 0.
Сначала вычислим дискриминант.
Мы видим, что а = 12, b = 7, c = 1.
Итак:
D = b2 – 4ac = 72 – 4 · 12 · 1 = 49 – 48 = 1.
D > 0. Значит, уравнение имеет корни (причем два корня), а значит, можно вычислять дальше.
Чтобы найти корни, применим формулу корней квадратного уравнения:
-b ± √D -7 ± √1 -7 ± 1
x = ———— = ———— = ————
2a 24 24
Находим оба значения x:
-7 + 1 -6 -1 1
x1 = ——— = —— = — = – —
24 24 4 4
-7 – 1 -8 -1 1
x2 = ——— = —— = — = – — .
24 24 3 3
1 1
Ответ: x1 = – —, x2 = – —
4 3
составим Алгоритм решения квадратного уравнения
Алгоритм решения квадратного уравнения
Решим одно изуравнений из дом.зад .с помощью формулы квадратного уравнения ………………………..
На доске показать решение учителю
IV Первичное закрепление материала
Закрепление № 128 (1,7) у доски и в тетраде
1.Решите уравнения (работа в группе)
Решение у доски 14 -5х - =0
- 1 ряд 2- 5х +2=0
- 2 ряд -8х - 84=0
- 3 ряд 0,8-4х + 5 =0
Из ответов составьте фамилию французского математика
- 2; - 7 Т
- 0,5; 2 В
- -2 ;0,5 С
- 2,5 Е
- 14; -6 И
VСтранички истории (слайды 15-19)
1. Франсуа Виет (1540-1603)
Знаменитый французский ученый. Он впервые установил зависимость между корнями и коэффициентами квадратного уравнения.
2. Кристиан Вольф
Впервые ввёл термин "квадратное уравнение" немецкий философ Кристиан Вольф знаменитый немецкий философ.
3. Сильвестр Джеймс Джозеф английский математик, Сильвестр Джеймс Джозеф, который ввёл термин "дискриминант".
VI Самостоятельная работа(слайды 20-21) или №134 1,3 Стр 53
Тест:
1) Найти дискриминант уравнения
1. 2у2+3у+1=0. 2. 2у2+5у+2=0.
А) 11; Б) 17; А) 41; Б) 9;
В)-5; Г)1. В)-11; Г) 21.
3. х2-6х+5=0. 4. х2-7х+12=0.
А) 16; Б) -56; А) -1; Б) -97;
В)-16; Г)56. В)1; Г) 97.
2) Сколько корней имеет уравнение?
1. х2-9х+14=0? 2. х2-8х+15=0?
А) два; Б) один; А) два; Б) один;
В)не имеет корней; В)не имеет корней;
Г)множество. Г) множество
3. 2х2+х+2=0? 4. Зх2+х+4=0?
А) два; Б) один; А) два; Б) один;
В) не имеет корней; В) не имеет корней;
Г) множество. Г) множество.
VII. Саба?ты ?орытындылау Подведение итога урока (слайд 22-23)
- Какие слова зашифрованы?
- Таиимдкисрнн
- Ниваренуе
- Фэкоцинетиф
- Ерокнь
- Что нового Вы узнали на уроке?
- Какой этап урока (станция) Вам понравился больше?
- Каков алгоритм решения квадратного уравнения?
- ?йге тапсырма беру задание на дом
п. 22 № 536(а,б,в) №538 (слайд 24)
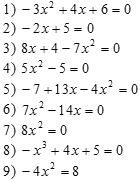 а доске задания:
а доске задания: 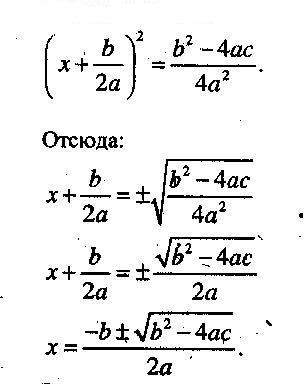
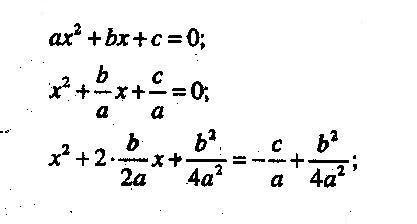
 Однако можно поступить проще, заметив, что в левой части данного уравнения стоит полный квадрат:
Однако можно поступить проще, заметив, что в левой части данного уравнения стоит полный квадрат: