16
Муниципальное образовательное учреждение
Ястребовская средняя общеобразовательная школа
Исследовательская работа по теме
«Различные способы линейных измерений»
Выполнила: Баньковская Ирина,
ученица 9 класса
Руководитель: Аликина Оксана Николаевна,
учитель математики, физики и
информатики
МКОУ Ястребовской СОШ
Ачинский район, 2014
Содержание
Введение ………………………………………………………………………….3
Глава I. Эволюция линейных измерений ……………………………………..4
§ 1. Линейные единицы измерения на Руси …………………………………..4
§ 2. Основные способы линейных измерений при помощи подручных
предметов …………………………..…..…………… .………………………...7
Глава II Геометрия на местности
§ 1. Несколько задач по определению расстояний на местности……..….9
§ 2. Современные измерительные приборы……………………………..…...11
§ 3. Определение высоты школы ……………..…………………………..…..13
§ 4. Результаты исследования …………………………………………………14
Литература ………………………………………………………………………15
Введение
Актуальность исследования
Для практических целей часто возникает необходимость производить различные измерения, геометрические построения на местности. Такие построения нужны и при строительстве зданий, и при прокладке дорог, и при различных измерениях объектов на местности. Как можно провести эти измерения? Можно ли их сделать подручными средствами? Какие инструменты нужны для измерений на местности?
Цель:
Исследование методов линейных измерений.
Объект исследования: линейные измерения
Предмет исследования: способы линейных измерений.
Гипотеза (познавательный вопрос)
Возможно ли произвести измерения недоступных объектов при помощи подручных средств или инструментов?
Задачи:
изучить историю единиц линейных измерений;
выяснить, какие способы линейных измерений существуют;
научиться применять разные способы линейных измерений на практике.
Методы решения основных задач:
описательный;
сопоставительный;
анализа и синтеза;
сравнительно – исторический;
Глава I. Эволюция линейных измерений
§ 1. Линейные единицы измерения на Руси
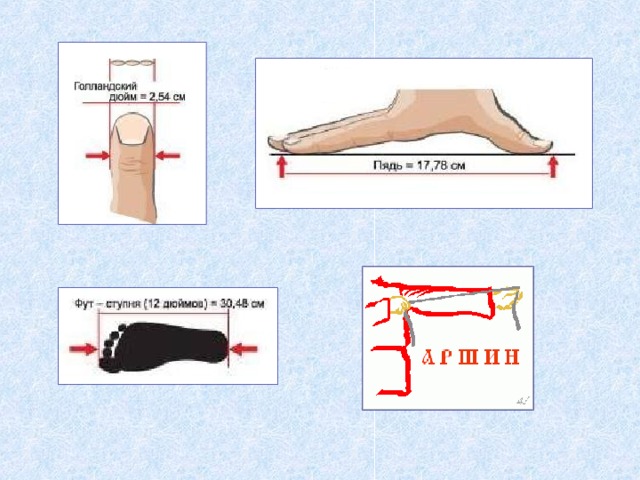
С древности, мерой длины всегда был человек: на сколько он протянет руку, сколько сможет поднять на плечи и т.д. Поэтому система древнерусских мер длины включала в себя следующие основные меры: версту, сажень, аршин, локоть, пядь и вершок. Большинство из этих мер связаны с человеком. Рассмотрим некоторые старинные меры длины. [1, c.23]
АРШИН - русская мера длины, равная, в современном исчислении 0,7112м. Аршином, так же, называли мерную линейку, на которую, обычно, наносили деления в вершках. Купцы, продавая товар, как правило, мерили его своим аршином (линейкой) или по-быстрому – отмеряя 'от плеча'. Чтобы исключить обмер, властями был введён, в качестве эталона – "казенный аршин", представляющий собой деревянную линейку, на концах которой клепались металлические наконечники с государственным клеймом.
ПЯДЬ – более мелкая величина - МАЛАЯ ПЯДЬ расстояние между концами расставленных большого и указательного (или среднего) пальцев = 17,78 см. БОЛЬШАЯ ПЯДЬ - расстояние между концами большого пальца и мизинца (22-23 см.). С 17-го века - длину равную пяди называли уже иначе – "четверть аршина", "четверть", "четь". Меньшие доли – два вершка (1/2 пяди) или вершок (1/4 пяди). Была ещё П Я Д Ь С КУВЫРКОМ ("пядень с кувырком", по Далю - 'п я д ь с кувыркой') - пядь с прибавкой двух суставов указательного палица = 27-31 см
САЖЕНЬ - одна из наиболее распространенных на Руси мер длины. Различных по назначению (и, соответственно, величине) саженей было больше десяти. "Маховая сажень" - расстояние между концами пальцев широко расставленных рук взрослого мужчины. " Косая сажен " - самая длинная: расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. Используется в словосочетании: "у него косая сажень в плечах " (в значении - богатырь, великан). Наименование с а ж е н ь происходит от глагола сягать (досягать). Сажень приблизительно равна 151,4 см. Существовали саженные мерные веревки и деревянные "складени", имевшие применение при измерении расстояний и в строительстве.
МАХОВАЯ САЖЕНЬ - расстояние между концами средних пальцев раскинутых в стороны рук - 1,76м. КОСАЯ САЖЕНЬ (первоночально "косовая") - 2,48м. Сажени употреблялись до введения метрической системы мер.
ЛОКОТЬ - расстояние от локтевого сгиба до конца вытянутого среднего пальца руки. Величина этой древнейшей меры длины, по разным источникам, составляла от 38 до 47 см. С 16-го века постепенно вытесняется аршином и в 19 веке почти не употребляется. Локоть широко применяли в торговле как особенно удобную меру. В розничной торговле холстом, сукном, полотном - локоть был основной мерой. В крупной оптовой торговле - полотно, сукно и прочее, поступали в виде больших отрезов — "поставов", длина которых в разное время и в разных местах колебалась от 30 до 60 локтей (в местах торговли эти меры имели конкретное, вполне определенное значение)
ВЕРШОК равнялся 1/16 аршина, 1/4 четверти. В современном исчислении - 4,44см. Наименование "Вершок" происходит от слова "верх". При определении роста человека или животного счёт велся после двух аршин (обязательных для нормального взрослого человека): если говорилось, что измеряемый был 15 вершков роста, то это означало, что он был 2 аршина 15 вершков, т.е. 209 см.
| Рост в Вершках | 1 | 3 | 5 | 7 | 9 | 10 | 15 |
| Рост в метрах | 1,47 | 1,56 | 1,65 | 1,73 | 1,82 | 1,87 | 2,09 |
ВЕРСТА - старорусская путевая мера (её раннее название - ''поприще''). Этим словом, первоначально называли расстояние, пройденное от одного поворота плуга до другого во время пахоты. Два названия долгое время употреблялись параллельно, как синонимы. До царя Алексея Михайловича в 1 версте считали 1000 саженей. При Петре Первом одна верста равнялась 500 саженей, в современном исчислении - 213,36 X 500 = 1066,8 м. "Верстой" также назывался верстовой столб на дороге. Величина версты неоднократно менялась в зависимости от числа сажен, входивших в неё, и величины сажени. Уложением 1649 года была установлена "межевая верста" в 1 тысячу саженей. Позже, в XVIII веке наряду с ней стала использоваться и "путевая верста" в 500 саженей ("пятисотная верста").
МЕЖЕВАЯ ВЕРСТА - старорусская единица измерения, равная двум верстам. Версту в 1000 сажен (2,16 км) употребляли широко в качестве межевой меры, обычно при определении выгонов вокруг крупных городов, а на окраинах России, особенно в Сибири - и для измерения расстояний между населенными пунктами.
Меры длины (употреблявшиеся в России после "Указа" 1835 г. и до введения метрической системы):
1 верста = 500 саженей = 50 шестов = 10 цепей = 1,0668 километра
1 сажень = 3 аршина = 7 фут = 48 вершков = 2,1336 метра
Косая сажень = 2,48 м. Маховая сажень = 1,76 м.
1 аршин = 4 четверти (пяди) = 16 вершков = 28 дюймов = 71,12 см (на аршин обычно наносили деления в вершках)
1 локоть = 44 см (по разным источникам от 38 до 47 cm)
1 фут = 1/7 сажени = 12 дюймов = 30,479 см
1 большая пядь = 1/2 локтя = 22-23 см - расстояние между концами вытянутого большого и среднего (или мизинца) пальцев.
"Пядень с кувырком" равен малой пяди плюс два или три сустава указательного или среднего пальца = 27 - 31 см.
1 вершок = 4 ноктя (по ширине - 1,1 см) = 1/4 пяди = 1/16 аршина = 4,445 сантиметра
- старинная русская мера длины, равная ширине двух пальцев (указательного и среднего).
1 перст ~ 2 см.
Новые меры [3, c.48] (введены с XVIII века):
1 дюйм = 10 линий = 2,54 см Название происходит от голландского - ''большой палец''. Равен ширине большого пальца или длине трех сухих зерен ячменя, взятых из средней части колоса.
1 линия = 10 точек = 1/10 дюйма = 2,54 миллиметра (пример: "трёхлинейка" Мосина - d=7.62 мм.) Линия - ширина пшеничного зерна, примерно 2,54 мм.
1 сотая сажени = 2,134 см
1 точка = 0,2540 миллиметра
1 географическая миля (1/15 градуса земного экватора) = 7 верст = 7,42 км (от латинского слова "милия" - тысяча (шагов))
1 морская миля (1 минута дуги земного меридиана) = 1,852 км
1 английская миля = 1,609 км
1 ярд = 91,44 сантиметра
Фут и дюйм, которыми пользовались в России, равны по величине английским мерам. Указ 1835 г. определил соотношение русских мер с английскими:
Сажень = 7 футам
Аршин = 28 дюймам
Этим указом упраздняется ряд единиц измерения (подразделения версты), и входят в употребление новые меры длины: дюйм, линия, точка, заимствованные из английских мер.
Только после революции в нашей стране были установлены современные единицы длины. Но до сих пор в современном русском языке старинные единицы измерения и слова, их обозначающие сохранились, в основном, в виде пословиц и поговорок
Поговорки:
- "Пишешь аршинными буквами" - крупно
- "Коломенская верста" - шутливое название очень высокого человека.
- "Косая сажень в плечах" - широкоплечий
§2. Основные способы линейных измерений при помощи подручных предметов
Для практических целей часто возникает необходимость производить геометрические построения на местности. Такие построения нужны и при строительстве зданий, и при прокладке дорог, и при различных измерениях объектов на местности. Можно подумать, что работа на ровной поверхности земли ничем, по существу, не отличается от работы циркулем и линейкой на обыкновенном листе бумаги.
Это не совсем так. Ведь на бумаге циркулем мы можем проводить любые окружности или их дуги, а линейкой - любые прямые. На местности же, где расстояния между точками довольно велики, для подобных действий понадобилась бы длинная веревка или огромная линейка, которые не всегда имеются под руками. Да и вообще чертить прямо на земле, какие бы то ни было линии - дуги или прямые - представляется весьма затруднительным. Таким образом, построения на местности имеют свою специфику.
Для нахождения расстояний, высот, глубин или других размеров реальных объектов не всегда можно обойтись непосредственным их измерением - во многих случаях такие измерения сопряжены с определенными трудностями, а то и вообще практически невозможны. Однако в своей деятельности человеку приходится порой задумываться над тем, как все-таки можно определить интересующую его величину и как сделать это точнее.
Основными измерительными «приборами», которые всегда имеются «под рукой», являются части тела человека. Например: шаг, пядь - размах пальцев, сажень - размах рук, уровень глаз (расстояние от земли до глаз) и т. д. . Важно следить за надежностью способа, чтобы избежать больших погрешностей, которые возникают при работе на местности. Для измерений небольших расстояний, не требующих высокой точности, чаще применяют деревянный или стальной складной метр, сантиметровую ленту, рулетку.
Более точные малые измерения выполняют штангенциркулем. С его помощью можно измерять диаметр отверстий и толщину деталей, имеющих размеры от нескольких миллиметров до нескольких дециметров.
Циркуль с регулируемым винтом можно использовать как для измерения, так и для разметки деталей. Он особенно незаменим в том случае, когда нужно разделить отрезок на несколько равных частей.
Для измерения и разметки отрезков применяют регулируемый рейсмус. Приложив этот инструмент к наружному ребру детали, можно с помощью риски обозначить необходимый размер или провести черту, параллельную ребру детали.
Если у вас нет под рукой никаких инструментов, то можно воспользоваться подручными предметами для измерения небольших расстояний, например монет или спичечным коробком.
И![]()
змерения при помощи подручных предметов.
| Предмет | Размер | Пример |
| 10 рублей | 27мм | 5 см – одна 10 рублевая + одна 2 рублевая монеты |
| 5 рублей | 25 мм | 5см – 2 монеты |
| 2 рубля | 23 мм |
|
| 1 рубль | 20 мм | 10 см – 5 монет |
| 50 копеек | 19 мм |
|
| 10 копеек | 17 мм | 4 см – одна 2 рублевая + одна 10 или 5 копеечная монеты |
| 5 копеек | 17 мм |
|
| 1 копейка | 15 мм |
|
| Спичечный коробок | 50×30,(50×35) | 15 см – 3 коробка |
Сделав измерения своей ладони и руки, мы легко можем применить эти данные, для каких либо измерений.
Измеряя какие-либо длины пальцами руки, лучше не отрывать руку от измеряемой поверхности, а приставлять один палец к другому, который затем снова вытягивать в заданном направлении (описанный процесс отдаленно напоминает движение гусеницы). Чтобы найти длину такого размаха своих пальцев, проще всего отложить вдоль какой-нибудь прямой одни или несколько десятков размахов пальцев, а затем поделить на их количество отложенную в результате длину.
Измерение углов с помощью подручных предметов. [4, c.56]
При измерении углов можно использовать подручные предметы (карандаш, спичечный коробок и т. п.), размеры которых известны в миллиметрах, а следовательно, и в тысячных на расстоянии 50 см от глаз.
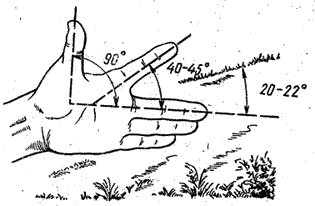
Приближенно определять углы на местности можно с помощью пальцев рук, удаленных от глаз на 50 см. Угол между большим и средним пальцами руки равен 90° (рис.1), а между средним и указательным - 40°. Зная это, можно определить крутизну ската. На рисунке крутизна ската равна 20 - 22°.
Глава II. Геометрия на местности
§ 1. Несколько задач по определению расстояний на местности
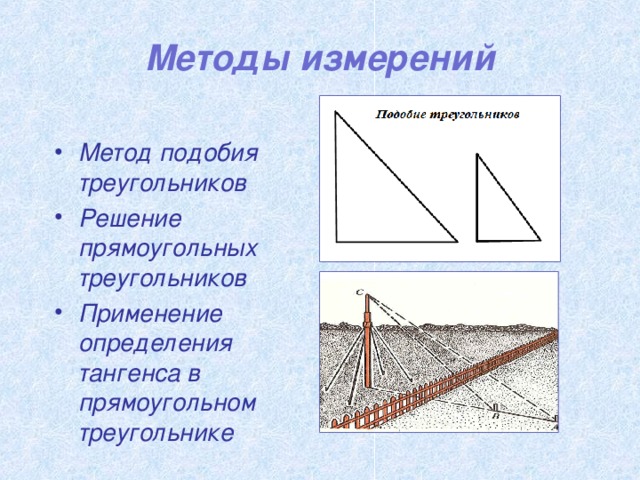
Для измерений больших расстояний на местности мы не всегда можем воспользоваться рулеткой. Ведь иногда надо измерить какое - нибудь расстояние, которое недоступно нам, тогда можно воспользоваться различными математическими методами. Рассмотрим некоторые из них. [2, c.102]
Задача 1. Определение высоты пирамиды Фалесом
Самый легкий и самый древний способ - без сомнения, тот, который греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Фалес, - говорит предание, - избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна также равняться длине отбрасываемой ею тени. Конечно, длину тени надо было считать от средней точки квадратного основания пирамиды; ширину этого основания Фалес мог измерить непосредственно. Однако способ Фалеса в указанном виде применим не всегда.
Задача 2. Задача Шерлока Холмса
Всемирно известный писатель Артур Конан Дойль был врачом. Но он очень хорошо, видимо, знал геометрию. В рассказе “Обряд дома Месгрейвов” он описал, как Шерлоку Холмсу нужно было определить, где будут конец тени от вяза, который срубили. Он знал высоту этого дерева ранее. Шерлок Холмс так объяснил свои действия: “… я связал вместе два удилища, что дало мне шесть футов, и мы с моим клиентом отправились к тому месту, где когда-то рос вяз. Я воткнул свой шест в землю, отметил направление тени и измерил ее. В ней было девять футов. Дальнейшие мои вычисления были уж совсем несложны. Если палка высотой в шесть футов отбрасывает тень в девять футов, то дерево высотой в шестьдесят четыре фута отбросит тень в девяносто шесть футов, и направление той и другой, разумеется, будет совпадать»
Задача 3. Определение на местности расстояний по линейным размерам предметов. [7, c.45]
Определение расстояний по линейным размерам предметов заключается в следующем. С помощью линейки, расположенной на расстоянии 50 см от глаза, измеряют в миллиметрах высоту (ширину) наблюдаемого предмета. Затем действительную высоту (ширину) предмета в сантиметрах делят на измеренную по линейке в миллиметрах, результат умножают на постоянное число 5 и получают искомую высоту предмета в метрах. Например, телеграфный столб высотой 6 м (см. рисунок) закрывает на линейке отрезок 10 мм.
Следовательно, расстояние до него: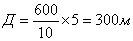
Точность определения расстояний по линейным величинам составляет 5-10% длины измеряемого расстояния.
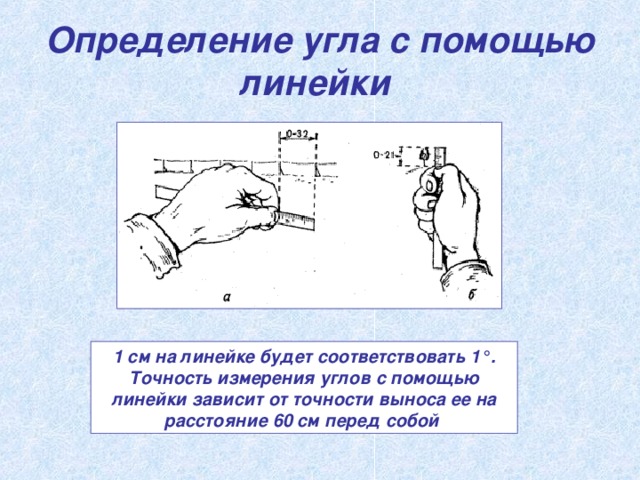
Задача 4. Определение угла с помощью линейки.
Для измерения угла в градусах линейка выносится перед собой на расстояние 60 см. В этом случае 1 см на линейке будет соответствовать 1°.
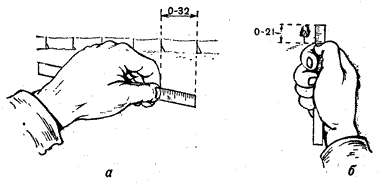
а - угол между столбами линии связи 0-32; б - угол на дерево 0-21
Точность измерения углов с помощью линейки зависит от точности выноса ее на расстояние 50 см перед собой.
Задача 5. Определение расстояний геометрическими построениями на местности. [6, c.68]
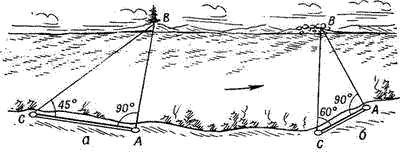
Этот способ может применяться при определении ширины труднопроходимых или непроходимых участков местности и препятствий (рек, озер, затопленных зон и т. п.). На рис.2 показано определение ширины реки построением на местности равнобедренного треугольника. Так как в таком треугольнике катеты равны, то ширина реки АВ равна длине катета АС. Точка А выбирается на местности так, чтобы с нее был виден местный предмет (точка В) на противоположном берегу, а также вдоль берега реки можно было измерить расстояние, равное ее ширине. Положение точки С находят методом приближения, измеряя угол АСВ компасом до тех пор, пока его значение не станет равным 45°.
§ 2. Современные измерительные приборы
С развитием производства возникает потребность в новых измерительных приборах. В ремонтных и отделочных работах постоянно возникает необходимость отметить точную горизонтальную и вертикальную линию, измерить высоту помещения, провести угловые измерения и т.п. В таких случаях наиболее подходящим средством для достижения требуемой цели будут приборы для линейных и угловых измерений и лазерные приборы. Вот несколько примеров:
- наклейка обоев, где требуется строго отметить вертикальную линию, вдоль которой наклеить первую полосу;
- навешивание полок, картин и т.п.;
- обшивка стен гипсокартонном, монтаж подвесных потолков;
- облицовка стен керамической плиткой;
- установка маяков для заливки стяжек или для штукатурных работ.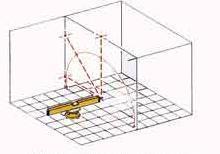 
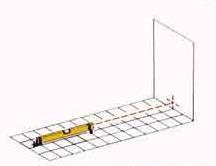
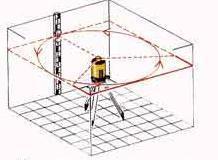
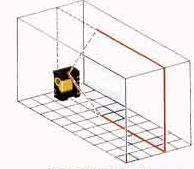
Достаточно направить лазерный прибор в нужную сторону и включить его, и вот уже перед глазами, четко видимая вертикальная или горизонтальная линия-ориентир. [5, c.63]
Лазерные приборы оснащены встроенным лазерным диодом, который испускает горизонтальный луч. Приборы имеют поворотный диск 360° (цена деления 1°) и могут быть установлены на штативе или настенном кронштейне; Совершенно ровный лазерный луч с успехом заменяет обычный отвес, спиртовой уровень, металлический угольник, строительную струну или шнур и даже рулетку, особенно на расстояниях до 200 метров.
Для измерений на местности нужны другие приборы, дающие хорошую точность измерений, они тоже имеют в своей основе лазерный луч, точную оптику.
|
А стролябия (позднелат. astrolabium, от греч. astron - звезда и labe - схватывание), угломерный прибор, служивший до 18 в. для определения широт и долгот в астрономии.
| 
Буссоль (франц. boussole), геодези- ческий инструмент для измерений горизонтальных углов между магнитным меридианом и направлением на какой-либо предмет |
|
Т еодолит, геодезический инструмент для определения направлений и измерения горизонтальных и вертикальных углов при геодезических работах, топографических и маркшейдерских съёмках, в строительстве и т. п.. Теодолит состоит из вращающегося вокруг вертикальной оси горизонтального круга (лимба) с алидадой |  Нивелир (от франц. niveler - выравнивать, niveau - уровень), геодезический инструмент для измерения превышения точек земной поверхности - нивелирования, а также для задания горизонтальных направлений при монтажных и т.п. работах. |
|
Т ахеометр (от греч. tachys, родительный падеж tachéos - быстрый и метр), геодезический прибор, применяемый при тахеометрической съёмке, для измерения на местности горизонтальных и вертикальных углов b и v
|  Приборы для измерения линий — стальные и тесьмяные рулетки, ленты (в том числе длиной до 1000 м для установления глубины шахт), дальномеры нитяные... |
§ 3. Определение высоты школы
С помощью подручных средств мы провели необходимые измерения на местности, чтобы определить высоту нашей школы. Рассмотрим получившиеся результаты. При этом считали, что этот объект недоступен.
В своей работе мы использовали измерительную линейку (длина 1,5 м), эклиметр, зеркало, шест.
Способ 1
Использования шеста известной длины для нахождения высоты школы.
А
В
С
Д
О1
О
1.Шест должен быть выше роста человека.
2.Шест и школа должны стоять «друг за другом» и их вершины
совпадают.
3. Измерим расстояния от человека до школы и до шеста
4.Измерим расстояние от земли до глаз человека и высоту шеста.
5.Используя подобие треугольников, найдем высоту школы
СД = 0,7 м, ДО = 2,1 м, ВО = 14,9 м, ОО1 = 1,6 м
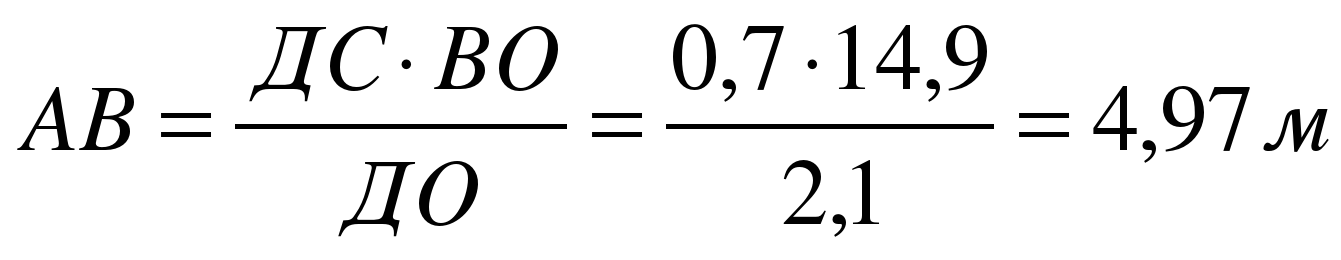
Высота школы равна АВ + ОО1 = 4,97 + 1,6 = 6,57 м.
Способ 2
Измерение высоты школы с помощью зеркала
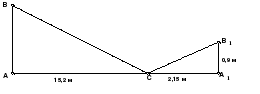
Положим зеркало на небольшом расстоянии от школы;
Подходим к зеркалу до тех пор, пока в нем не увидим верхушку крыши;
Замеряем расстояние от школы до зеркала и от зеркала до точки, где стоим;
И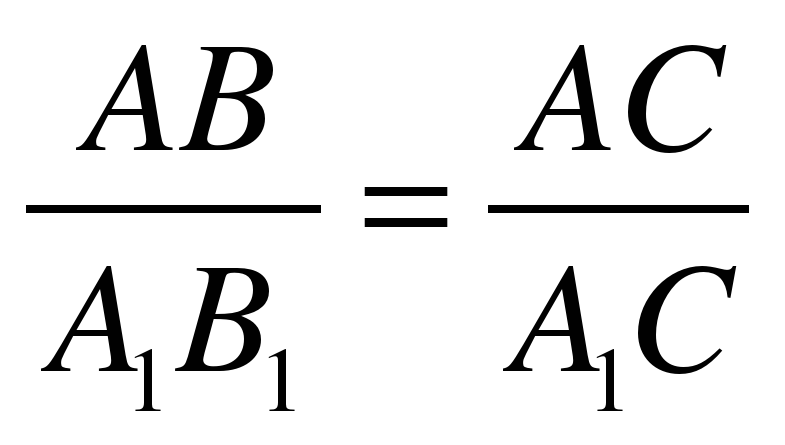
змеряем рост смотрящего до глаз;
Из полученных данных получим отношение
Высота школы 6,36 м.
Способ 3
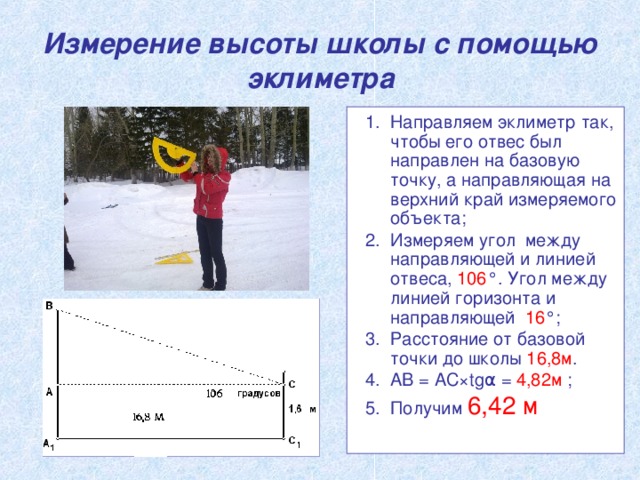
Измерение высоты школы с помощью эклиметра
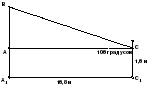
Направляем эклиметр так, чтобы его отвес был направлен на базовую точку, а направляющая на верхний край измеряемого объекта;
Измеряем угол между направляющей и линией отвеса, 106°. Угол между линией горизонта и направляющей 16°;
Расстояние от базовой точки до крыльца 16,8 м.
АВ = АС · tgα + СС1 (расстояние от земли до уровня глаз);
АВ = 16,8 · 0,2869 + 1,6
Высота школы 6,42 м.
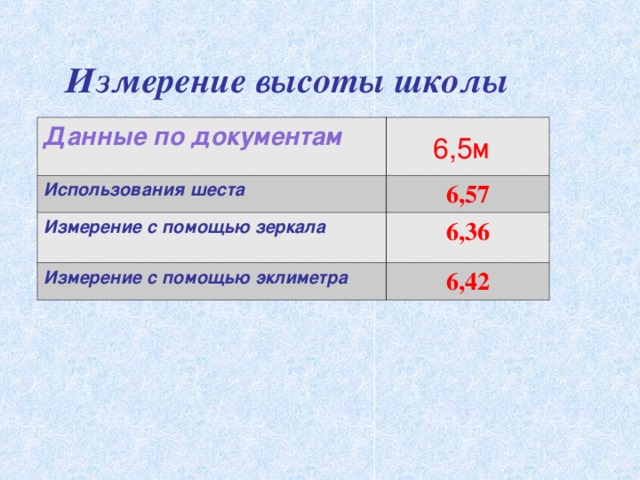
Измерение высоты школы
| Данные по документам | 6,5 |
| Использования шеста | 6,57 |
| Измерение с помощью зеркала | 6,36 |
| Измерение с помощью эклиметра | 6,42 |
§ 4. Результаты исследования
Для достижения цели были проведены 3 разных способа.
Погрешность вычислений составляет от 8 до 14 см.
Большая погрешность получилась при использовании зеркало, из – за кривизны зеркало.
Подручными средствами возможно определить размеры объекта, даже недоступного.
Литература
1. Виленкин Н.Я., Шибасов Л.Т., Шибасова З.Ф. За страницами учебника
математики: Арифметика. Алгебра. Геометрия. - М.: Просвещение:
АО «Учеб. мет.», 1996.
2. Ганьшин В.Н. Простейшие измерения на местности, М., 1973 - 126 с.
3. Депман И.Я., Виленкин Н. Я. За страницами учебника математики. - М. -:
Просвещение, 1989.
4. Занимательная алгебра. Занимательная геометрия. / Я.И. Перельман. -
Ростов Н/Д: ЗАО «Книга», 2005.
5. Иваньков П.А. Основы геодезии , топографии и картографии.-М., 1972
6. Иванов П.А. Технические измерения М., 1964
7. Сергеев И.Н., Олехник С.Н., Гашков С.Б. Примени математику. - М.,
Наука, 1989.
