
Скажи мне, и я забуду.
Покажи мне, и я запомню.
Позволь мне сделать, и это станет моим навсегда.
(китайская пословица)
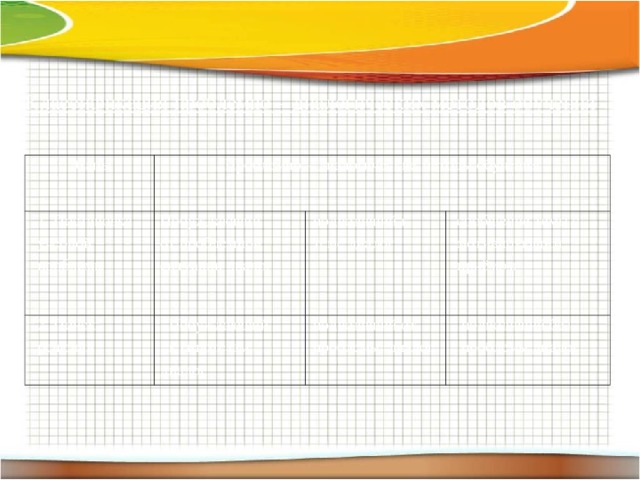
Классификация проблемно – диалогических методов обучения
Этапы
Проблемно – диалогические методы обучения
1. Постановка
учебной проблемы
Побуждающий
от проблемной
ситуации диалог
2. Поиск решения
подводящий к
теме диалог
Побуждающий
к гипотезам диалог
сообщение темы с
мотивирующим
приёмом
подводящий от проблемы диалог
подводящий без
проблемы диалог

МЕТОДЫ ПОСТАНОВКИ УЧЕБНОЙ ПРОБЛЕМЫ
- Побуждающий от проблемной ситуации диалог.
- Подводящий к теме диалог.
- Сообщение темы с мотивирующим приемом .

- Побуждающий от проблемной ситуации диалог.
Проблемная ситуация со столкновением мнений
учеников класса создается вопросом
или практическим заданием на новый материал.
Побуждение к осознанию противоречия осуществляется
репликами: «Вопрос был один?
А мнений сколько?» или «Задание было одно?
А выполнили вы его как?».
И далее общий текст: «Почему так получилось?
Чего мы еще не знаем?».
Побуждение к формулированию проблемы
осуществляется одной из реплик по выбору.

6 класс, тема:
«Сложение и вычитание дробей с разными знаменателями».
Учащимся постепенно предлагается выполнить действия с дробями:
- Какие ответы у вас получились?
- Смогли ли вы выполнить два последних действия?
- Если смогли, то какие ответы вы получили? Если нет, то почему?
- Какие дроби вы уже умеете складывать и вычитать?
(дроби с одинаковыми знаменателями)
- Можно ли данные дроби заменить дробями с одинаковыми знаменателями? (можно)

7 класс: тема:
«Умножение степеней с натуральным показателем».
Посмотрите на примеры на доске:
а 3 + а 5 а 3 ∙ а 5 (а 3 ) 5 а 3 – а 5 а 5 : а 3
- Как вы думаете, какие действия можно выполнять со степенями?
(мнения в классе разделяются).
- Вопрос был задан один, а смотрите сколько ответов вы на него дали.
- Так чего же мы еще не знаем?

Проблемная ситуация с противоречием между житейским,
т.е. ограниченным или ошибочным представлением
учеников и научным фактом.
Сначала учитель выявляет житейское представление
учеников вопросом или практическим
заданием « на ошибку » . Затем сообщением, экспериментом, расчетами или наглядностью предъявляет научный факт. Побуждение к осознанию противоречия
осуществляется репликами: « Вы что думали сначала?
А что оказывается на самом деле? » .
Побуждение к формулированию проблемы
осуществляется одной из реплик по выбору.

5 класс, тема: « Решение задач на проценты » .
Учащимся предлагается решить задачу:
« Предположим, цена стиральной машины была А рублей. Затем цена повысилась на 15%, а к Новому году снизилась на 15%. Изменилась ли цена стиральной машины? »
(учащиеся предполагают, что цена товара не изменилась – житейское представление)
В ходе дальнейших рассуждений выясняется противоречие между житейским представление учащихся и реальной ситуацией.
- Что вы предположили?
- А как оказалось на самом деле?
- Значит чему мы сегодня должны научиться?

7 класс, тема « Параллельные прямые » .
- Параллельны ли горизонтальные прямые?
- Как вы думали?
- А как оказалось на самом деле?
- Всегда ли возможно определить параллельность прямых « на глаз » ?
- Познакомимся с признаками параллельности прямых?

Проблемная ситуация с противоречием между
необходимостью и невозможностью выполнить
задание учителя создается практическим заданием,
не сходным с предыдущим.
Побуждение к осознанию проблемы осуществляется
репликами: « Вы смогли выполнить задание?
В чем затруднение? Чем это задание не похоже
на предыдущее? » . Побуждение к формулированию
проблемы осуществляется одной из реплик по выбору.

5 класс, тема: « Умножение десятичных дробей » .
Учащимся предлагается выполнить действия:
0,5763 · 87
5, 763 · 87
57, 63 · 87
576,3 · 8,7
- Смогли ли вы выполнить последнее действие? (нет)
- Почему?
- Чем последнее действие отличается от предыдущих?
- Чем, по вашему мнению, мы будем заниматься сегодня?

- Подводящий к теме диалог.
Вопросы и задания могут различаться по характеру
и степени трудности, но должны быть посильными
для учеников. Последний вопрос содержит обобщение
и позволяет ученикам сформулировать тему урока.
По ходу диалога необходимо обеспечивать
безоценочное принятие ошибочных ответов учащихся.

5 класс, тема « Деление десятичных дробей »
- На какие числа вы уже умеете делить десятичную дробь?
(на натуральные)
- А как вы думаете, на какие еще числа можно делить десятичные дроби?
(на десятичные дроби)
- Какова, по вашему мнению, тема нашего урока?
(деление десятичных дробей)
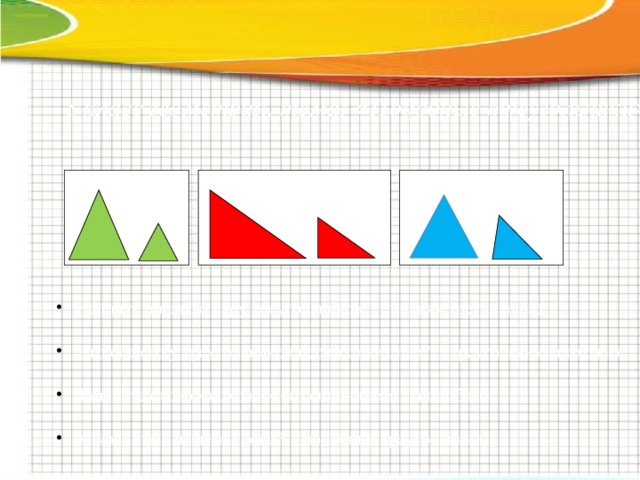
8 класс геометрия, тема: « Подобные треугольники » .
- Найдите лишнюю пару треугольников. (лишняя третья пара).
- Что общего у треугольников первых двух пар? (треугольники похожи)
- Замените слово « похожи » его синонимом. (подобны).
- Какова тема нашего урока? (подобные треугольники)

- Сообщение темы с мотивирующим приемом .
Суть метода заключается в том, что учитель
предваряет сообщение готовой темы либо
интригующим материалом (прием « яркое пятно » ),
либо характеристикой значимости темы
для самих учащихся (прием « актуальность » ).
В некоторых случаях оба мотивирующих приема
используются одновременно.

6 класс, тема: « Координатная плоскость » .
В начале урока учитель демонстрирует классу хорошо знакомые предметы, например, шахматную доску, глобус, билет в театр.
- Что объединяет все эти предметы? (они помогают определить
положение (место) человека в зрительном зале, на планете
или фигуры на шахматной доске).
- Как описать положение точки на плоскости?
(ввести координаты на плоскости).
- Какова же тема урока? (координаты на плоскости).

8 класс, тема: «Теорема Виета».
Урок начинается с исторической зарисовки.
XVI век. Франция. Адвокат и советник короля Генриха III Франсуа Виет, будучи выдающимся математиком, сумел раскрыть ключ шифра, состоявшего из 500 знаков, с помощью которого
враги короля вели переписку с испанским двором. Но среди математиков
Виет известен своей теоремой о свойствах корней квадратного уравнения.
А какое это свойство вы увидите сами.
Решите квадратное уравнение:
1 группа – 5х² – 6х + 1 = 0
2 группа – 6х² – 5х – 1 = 0
3 группа – х² – 5х + 6 = 0
- Найдите сумму и произведение корней уравнения.
- Что интересного вы заметили?

5 класс, тема: « Проценты » .
Учащимся предлагается решить задачу:
« Вы хотите купить телефон. В магазине интересующая Вас модель стоит 4500 рублей,
но в магазине на нее предлагают скидку в 15%. Какую сумму Вы должны заплатить? »
- Можете ли вы решить эту задачу?
(Нет, мы не знаем, что такое процент).
- Хотите ли вы это узнать?
- А как вы думаете, где вам пригодятся эти знания?

МЕТОДЫ ПОИСКА РЕШЕНИЯ УЧЕБНОЙ ПРОБЛЕМЫ.
- Побуждающий к выдвижению и проверке гипотез диалог.
- Подводящий к знанию диалог.

- Побуждающий к выдвижению и проверке гипотез диалог.
Побуждающий к выдвижению и проверке гипотез
диалог представляет собой сочетание
специальных вопросов, стимулирующих
учеников выдвигать и проверять гипотезы.

7 класс, тема: « Сумма углов треугольника » .
Учащимся предлагается измерить углы треугольника и найти их сумму.
1 группа – остроугольный треугольник.
2 группа – прямоугольный треугольник.
3 группа – тупоугольный треугольник.
- Чему равна сумма углов Вашего треугольника?
- Как вы думаете, в любом ли треугольнике такая сумма углов?
- Давайте найдем ответ на этот вопрос на сегодняшнем уроке.
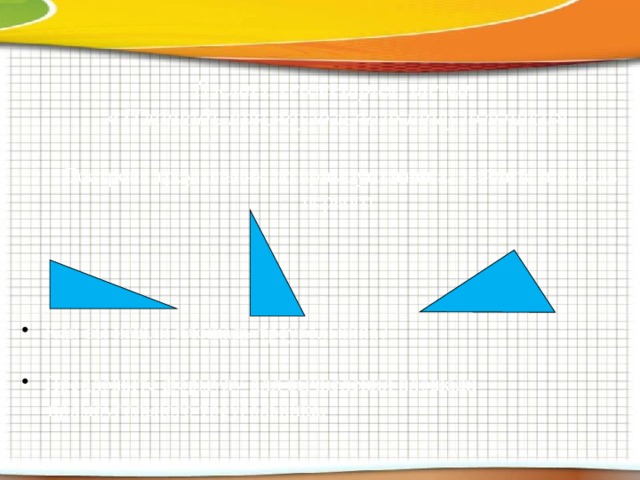
8 класс геометрия, тема:
« Площадь прямоугольного треугольника » .
Достроив треугольник до прямоугольника, найдите площадь первого.
- Как вы нашли площадь треугольника?
- Предложите формулу для вычисления площади
прямоугольного треугольника.

6 класс, « Признаки делимости на 10, на 5 и на 2 » .
Распределите числа на три столбика:
а) делятся на 2; б) делятся на 5; в) делятся на 10.
2354, 4535, 7892, 1270, 7895, 9766, 3370, 1098, 9945, 6185.
- Как вы определили число в первый столбик, во второй столбик,
в третий столбик?
- Какие числа делятся на 2, делятся на 5, делятся на 10?

- Подводящий к знанию диалог.
Представляет собой систему вопросов и заданий,
обеспечивающих формулирование ( « открытие » )
нового знания учениками. Подводящий диалог
можно развернуть как от поставленной учебной
проблемы, так и без нее. В первом случае учитель
любым методом обеспечивает постановку проблемы,
во втором случае этот этап урока пропускается вообще.
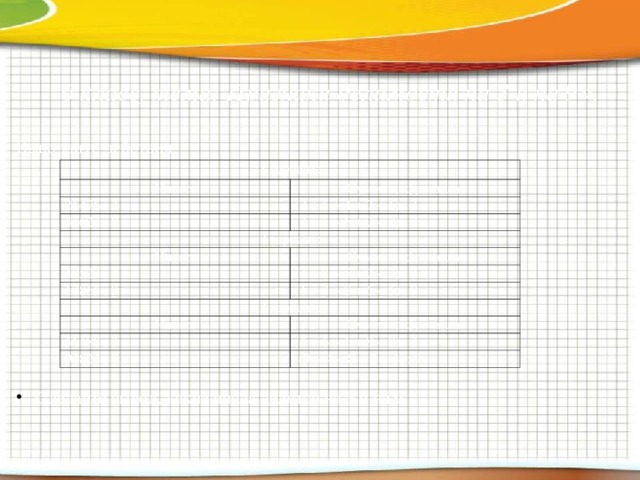
6 класс, тема: Признаки делимости на 3 и на 9 » .
Выполните действия:
- Сделайте вывод, какие числа делятся на 3 и на 9.
1 вариант:
Число:
Сумма цифр числа:
25476 : 3
(2 + 5 + 4 + 7 + 6) : 3
35623 : 9
(3 + 5 + 6 + 2 + 3) : 9
2 вариант:
Число:
Сумма цифр числа:
48523 : 3
17865 : 9
(4 + 8 + 5 + 2 + 3) : 3
(1 + 7 + 8 + 6 + 5) : 9
3 вариант:
Число:
Сумма цифр числа:
56188 : 3
(5 + 6 + 1 + 8 + 8) : 3
94824 : 9
(9 + 4 + 8 + 2 + 4) : 9

9 класс алгебра, тема:
« Разложение на множители квадратного трехчлена » .
- Сравните конечное выражение второго столбика и квадратное уравнение.
- Сравните корни уравнения с числами в скобках.
Решите квадратное уравнение:
Раскройте скобки:
3х 2 – 7х – 6 + 0
3(х – 3)(х + 2 /3 )

Метод проблемного обучения эффективно способствует
формированию у учащихся математического склада мышления, интереса к предмету, прививает навыки исследовательской работы и желание самостоятельно решать возникшие ситуации. Он направлен на формирование мировоззрения учащихся, их познавательной самостоятельности, устойчивых мотивов учения и мыслительных способностей.
















































