Построение углов без транспортира

Предложен способ построения углов без транспортира на клетчатой бумаге

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Построение углов без транспортира»

Научно - исследовательская работа

Предмет математика

Тема работы

«Построение углов без транспортира»

Выполнила:

Мурзинова Ксения Евгеньевна

учащаяся 8 класса

МБОУ «Усть-Нерская гимназия»

Руководитель:

Аршина Алена Геннадьевна

учитель математики высшей квалификационной категории

МБОУ «Усть-Нерская гимназия»

2020 год

Оглавление

Введение………………………………………………………………….3
Основная часть
1. История геометрических измерений углов………………..……5
2. Экспериментальная часть…………… …………………………..7
3. Практическое применение….…………………………………….7
Заключение……………………………………………………………...12
Литература ………………………………………………………………13

Введение

Почему тетради по математике в клетку? Наверное, чтобы удобнее было записывать в столбик числа. А еще, чтобы легче было чертить. Клеточки на бумаге позволяют многие построения проводить только с помощью одной линейки, причем на этой линейке может даже не быть делений. Мы уже можем строить на клетчатой бумаге отрезок заданной длины, прямоугольник, если известна его ширина и длина, квадрат с известной стороной. То есть обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения геометрических фигур.

Стало интересно, а можно ли построить параллелограмм, трапецию, треугольник? У всех этих фигур стороны проходят не по линиям сетки клетчатой бумаги, а пересекают их. Или, можно сказать, стороны находятся под углом друг к другу (отличного от 90). Поэтому, в первую очередь, мы должнынаучиться строить углы, используя только клетки.

Цель: найти способ построения углов без транспортира на клетчатой бумаге.

Задачи:

построить острые углы на клетчатой бумаге (от 10 до 80, кратных 10) и исследовать их расположение по отношению к узлам сетки;
составить таблицу решений исследуемой задачи;
проверить полученные результаты с помощью ПО GeoGebra
определить группы задач, которые можно решить с помощью исследованного метода построения углов;

Объект исследования: острые углы с градусной мерой, кратной 10;

Предмет исследования: процесс построения углов на клетчатой бумаге без использования транспортира;

Гипотеза: можно предположить, что существуют углы разных градусных мер, которые можно построить без транспортира, пользуясь только линейкой без мерных делений и клетчатой бумагой;

Практическая значимость:

Для построения углов, с градусными мерами, кратными 10 не требуется наличие транспортира;

С помощью предложенного метода можно выполнять чертежи геометрических фигур (треугольников, трапеции) с заданными мерами углов;

Данный метод позволяет начертить геометрические фигуры на местности или на бумаге большого формата, так как размер клетки может быть произвольным.

Новизна работы:

описанный метод построения углов без транспортира не используется на уроках; нет описания этого приема и в математической литературе.

Основная часть

Первые задачи на построение углов возникли в глубокой древности. Возникли они из хозяйственных потребностей человека. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией. Первые греческие ученые, которые занимались решением геометрических задач на построение, были: Фалес Милетский (624 – 547 гг. до н.э.), Пифагор (ок. 580 – 500 гг. до н.э.), Платон (427 – 347 гг. до н.э.). Платон и его ученики считали построение геометрическим, если оно выполнилось при помощи циркуля и линейки, то есть путем проведения окружностей и прямых линий. Если же в процессе построения использовались другие чертежные инструменты, например транспортир, то построение не считалось геометрическим. Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии. Известны приборы для измерения углов …

Экспериментальная часть

Для проведения исследования на листке клетчатой бумаги построили острые углы, начиная от 10 до 80, с интервалом в 10. Центр угла был расположен в узле клетки. Один из лучей, образующих угол, провели горизонтально слева направо. Далее с помощью транспортира начертили лучи для всех исследуемых углов.

Если второй луч проходил точно через узел клеток, то информацию об этом угле заносила в таблицу. Положение «контрольного» узла относительно вершины данного угла отмечалось следующим образом: сначала указывалось количество целых клеток вверх, затем вправо.

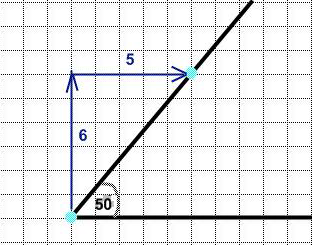
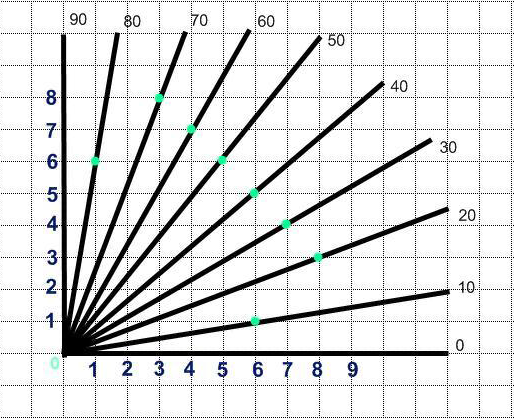
Расположение «контрольных» точек острых углов, кратных 10

В результате получилась такая таблица

Для углов от 20 до 70 количество клеток вверх на единицу превышает количество десятков в градусной мере угла. Причем сумма клеток вверх и вправо для всех этих углов равна 11.

Но можно ли считать найденные числа точными?

Погрешность измерения

Величина острого угла	Вверх	Вправо	Geo Gebra	Погрешность измерения
10	1	5	11,31	(10-11,31)/10= 0,131
20	3	8	20,56	0,028
30	4	7	29,74	0,0086
40	5	6	39,81	0,0048
50	6	5	50,19	0,0038
60	7	4	60,26	0,0043
70	8	3	69,44	0,008
80	5	1	78,69	0,016

Вывод: Средняя погрешность измерения составила 0,03. Это небольшое отклонение от точного значения, поэтому найденные значения в таблице можно считать достаточно близкими к точным. Значит по этим точкам можно строить углы.

Анализ данных в таблице

Чтобы построить угол без транспортира достаточно запомнить только точку для угла в 10 – (1;6), и для угла 80 - ей служит противоположная (6;1).

А все остальные «контрольные» точки лучей (для углов от 20 до 70, кратных 10) подчиняются несложному правилу, которое я сформулировала сама:

Если прибавить к числу десятков искомого угла единицу, то получим количество клеток по вертикали.

Если это число отнять от 11, то получим количество клеток по горизонтали от вершины угла.

Например, для построения угла в 70 нужно отступить 8 (7+1) клеток по вертикали и 3 (11-8) клетки по горизонтали в сторону первого луча.

Анализ данных в полученной таблице еще раз убеждает нас в существовании красоты, закона симметрии и порядка в науке математике.

Практическое применение результатов

1.Построение тупых углов от 0 до 180 с шагом 10

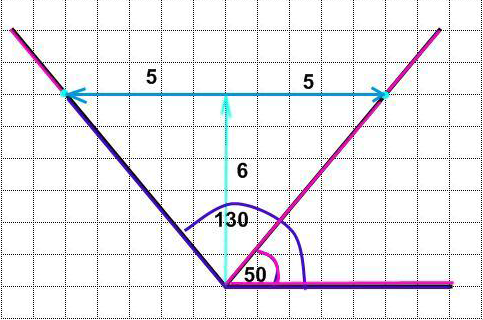
Смежные углы имеют общий луч. Поэтому для построения тупых углов можно пользоваться «контрольной» точкой смежного ему острого угла из таблицы. Только отсчет клеток по горизонтали выбирается впротивоположном горизонтальному лучу направлении (в нашем случае влево).

2.Построение треугольника, трапеции, шестиугольника

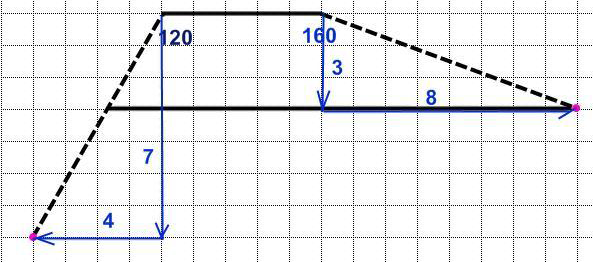
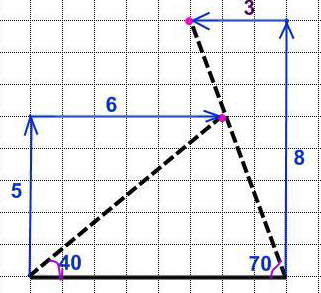
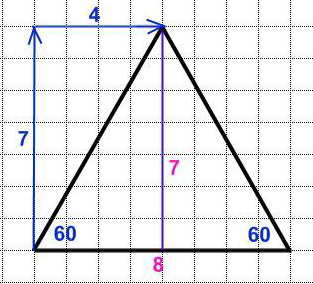
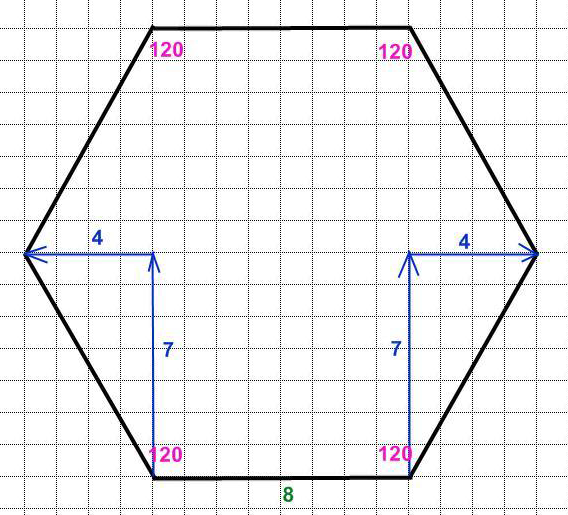
Заключение

Построение углов очень интересное и познавательное занятие, совсем не сложное и трудоемкое, как может показаться на первый взгляд. Мы выяснили, что:

1. Обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения углов.

2. Лучи, образующие любой угол, с градусной мерой, кратной 10, связаны с определенными узлами клеток на бумаге.

3. Полученные результаты можно использовать для построения трапеций и треугольников с заданными мерами углов без использования транспортира.

Метод построения углов на клетчатой бумаге актуален для школьников, так как все задачи оформляются на листке тетради в клетку и большинство задач в учебнике геометрии связано с построением фигур с углами, градусная мера которых кратна 10.

Всем, кто уже приступил к изучению геометрии, можно в качестве эксперимента попробовать использовать результаты моего исследования при построении углов и фигур на клетчатой бумаге без применения транспортира.

Литература и интернет-источники.

1. Л.С. Атанасян. Геометрия 7-9: Учеб. Для общеобразовательных учреждений-М.: Просвещение, 2010-384 с.:ил.

2. http://allencyclopedia.ru/17254 Большая Советская энциклопедия/ Геодезические инструменты.