ПрактическАЯ РАБОТА№ 3
Тема: «Основные правила дифференцирования. Вычисление производных логарифмических, показательных и тригонометрических функций»
Цели:
- повторить основные формулы и правила дифференцирования;
- научиться вычислять производные логарифмических, показательных и тригонометрических функций.
Оснащение занятия: конспект лекций.
Критерии оценок
оценка «5» ставится за верное выполнение всех заданий работы
оценка «4» ставится за выполнение задания 1 и верное решение любых пяти примеров
оценка «3» ставится за выполнение задания 1 и верное решение любых четырех примеров
Порядок выполнения работы
Задание 1.
- Ознакомиться с лекцией № 4
- Выписать в тетрадь формулы и правила для вычисления производных
- Записать в тетрадь решение рассмотренных примеров
Задание 2.
Решить примеры для самостоятельного решения
Лекция 4.
Тема « Производная и дифференциал.
Основные правила дифференцирования»
Производной функции y = f(x) в точке x (производной первого порядка) называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
Если этот предел конечный, то функция y = f(x) называется дифференцируемой в точке x; в противном случае (т. е. если он не существует или равен бесконечности) – недифференцируемой. В том случае, когда предел есть бесконечность, говорят, что функцияy = f(x) имеет в точке xбесконечную производную.
Дифференциалом dy функцииy = f(x) (дифференциалом первого порядка) называется главная часть её приращения, пропорциональная приращению независимой переменной.
Дифференциал dxнезависимой переменной x равен её приращению
dx =
Дифференциал любой дифференцируемой функции y = f(x) равен произведению её производной на дифференциал независимой переменной:
dy = dx
Это соотношение остаётся в силе и тогда, когда x есть функция другого аргумента – в этом заключается инвариантность формы первого дифференциала. Из формулы dy = dx получаем =, т. е. производная первого порядка функции y = f(x) равна отношению первого дифференциала функции к дифференциалу её аргумента.
Основные правила дифференцирования:
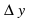 функции к приращению аргумента
функции к приращению аргумента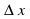 , когда последнее стремится к нулю:
, когда последнее стремится к нулю: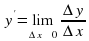
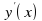 dx
dx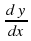 , т. е. производная первого порядка функции y = f(x) равна отношению первого дифференциала функции к дифференциалу её аргумента.
, т. е. производная первого порядка функции y = f(x) равна отношению первого дифференциала функции к дифференциалу её аргумента.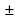 v)'=u'
v)'=u' 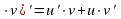 - производная произведения
- производная произведения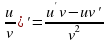 - производная дроби
- производная дроби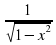
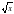 )' =
)' = 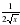 12. (arctg x) ' =
12. (arctg x) ' =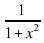
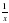 )' = -
)' = -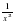 13. (arcctg x) ' =-
13. (arcctg x) ' =- )' = пх
)' = пх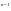 14. (
14. (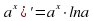
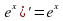
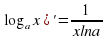
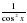 17. (lnx)'=
17. (lnx)'=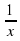
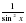
 3x2 + 9
3x2 + 9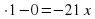 2 + 18x +4
2 + 18x +4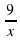 + 4
+ 4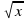 + 17x4 Найти: y'(x)
+ 17x4 Найти: y'(x)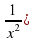 + 4
+ 4 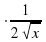 +17
+17 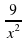 +
+ 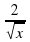 + 68x3
+ 68x3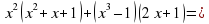
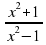 Найти: y'(x)
Найти: y'(x)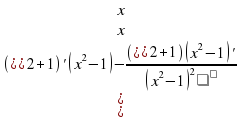 =
= 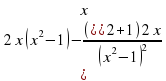 =
=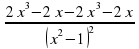 =
= 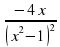
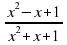 Найти: y'(1). Решить самостоятельно.
Найти: y'(1). Решить самостоятельно.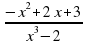 Найти: y'(2). Решить самостоятельно.
Найти: y'(2). Решить самостоятельно.