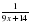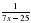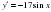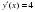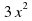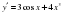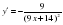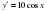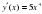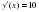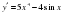Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Методическая разработка урока математики на тему «Вычисление производных»
Цели урока:
1. Образовательные:
а) закрепить навыки нахождения производных;
б) обобщить знания обучающихся о правилах нахождения производных функций;
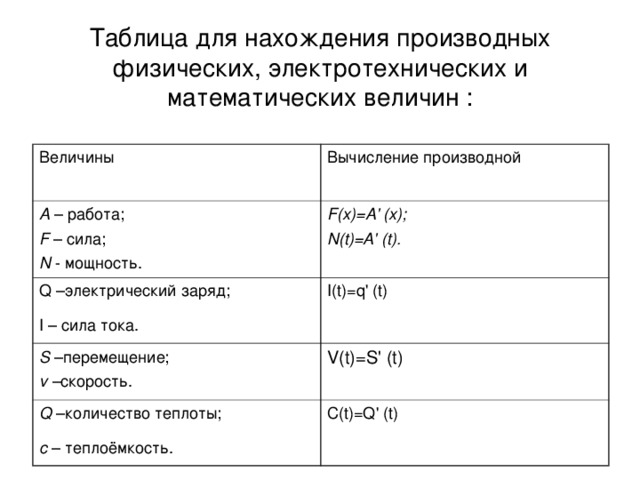
в) сформировать умения и навыки использования вычисления производных для вычисления различных величин при решении прикладных задач и задач производственной направленности.
2. Развивающие:
а) развитие профессиональных качеств обучающихся (умений применять полученные знания на практике);
б) развитие познавательных умений и мышления (выделять главное, анализировать, сравнивать, определять и объяснять понятия).
3. Воспитательные:
а) воспитание навыков самостоятельной работы;
б) воспитание дисциплинированности;
в) воспитание эстетических взглядов.
Тип урока: комбинированный
Повторение пройденного материала:
Назовите формулы для производных элементарных функций.(слайд 6)
Студенты:
1.
2.
3.
4.
5.
6.
7.
Назовите формулы для производных тригонометрических функций.
Студенты:
1.
2.
3.
4.
Назовите правила вычисления производных.
Обучающийся:
Основные правила дифференцирования
Пусть, тогда:
7. Перед Вами несколько функций.( слайд 7)
Давайте найдём их производные.
a) f(x)= 4tgx
Решение:
б) y=
Решение:
в) y=
Решение:
г) f(x)=
Решение:
д) f(t)=2sint
Решение:
8. Теперь перейдем к самостоятельной работе.
Самостоятельная работа. (слайд 8 название)
I Вариант II Вариант
Найдите производные функций: Найдите производные функций:
1) y=17cosx 1) y=10sinx
2) y=
2) y=
3) y=x^3+24
3) y=
4) y=3sinx+
4) y= +4cosx
5) y=
5) y =
Решение примеров из самостоятельной работы.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Метод разраб вычисление производных 1»
Просмотр содержимого презентации
«Презентация к Вычисление производных»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1540 руб.
2560 руб.
1800 руб.
3000 руб.
1510 руб.
2510 руб.
1430 руб.
2380 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

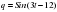 .
.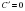
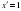
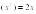
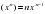
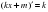
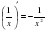
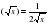
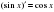
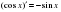
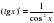
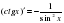
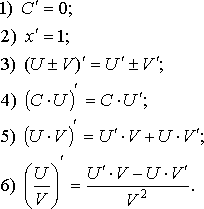
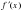
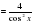
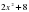
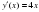
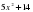
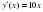
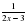
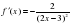
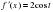
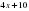
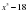
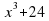
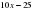
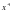
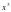 +4cosx
+4cosx