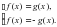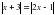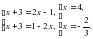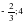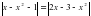Материал предназначен для учащихся 9-11 классов. Работа содержит краткую теорию и подробный разбор решения уравнений содержащих модули. Ознакомившись с данной работой учащиеся приобретут навыки и умения решать уравнения различного уровня сложности, содержащие модули и смогут проверить усвоение своих знаний.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Модули. Решение уравнений.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Модули. Решение уравнений. »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
1970 руб.
2820 руб.
2100 руб.
3000 руб.
1760 руб.
2510 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
 Модули. Решение уравнений. Плотникова Надежда Михайловна
Модули. Решение уравнений. Плотникова Надежда Михайловна
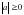
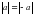
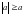
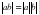
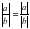 ,
, 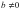

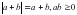
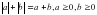
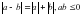
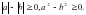
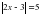
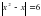
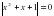
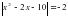
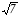
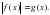
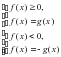
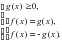
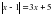
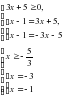

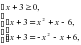
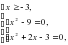
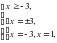
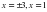
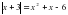
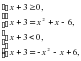
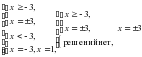
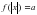 .
.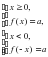
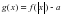 . Нули этой функции будут существовать парами противоположных чисел: если х = а – корень, х = -а -тоже корень этого уравнения. Поэтому достаточно решить лишь одну из систем 1 способа и добавить в ответ числа, противоположные найденным корням.
. Нули этой функции будут существовать парами противоположных чисел: если х = а – корень, х = -а -тоже корень этого уравнения. Поэтому достаточно решить лишь одну из систем 1 способа и добавить в ответ числа, противоположные найденным корням.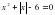
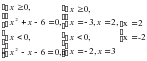
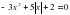
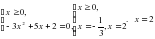
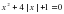
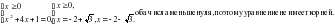 Ответ: корней нет.
Ответ: корней нет.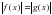 .
.