В презентации даётся определение обратных тригонометрических функций, указываются их свойства, а, также построены их графики.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Свойства и графики обратных тригонометрических функций
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Свойства и графики обратных тригонометрических функций»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1720 руб.
2860 руб.
1720 руб.
2860 руб.
1720 руб.
2860 руб.
1900 руб.
3170 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


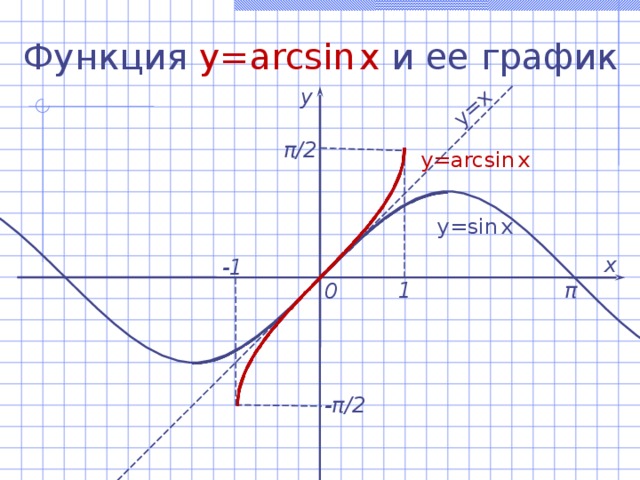
![Функция y=arcsin x и ее свойства Если |а| ≤ 1 , то arcsin а – это такое число из отрезка [- π /2 ; π /2 ] , синус которого равен а . Если |а| ≤ 1 , то arcsin а = t sin (arcsin a) = a sin t = а , - π /2 ≤ t ≤ π /2 ;](https://fsd.kopilkaurokov.ru/up/html/2017/10/06/k_59d75c1c3e195/img_user_file_59d75c1cb3536_2.jpg)

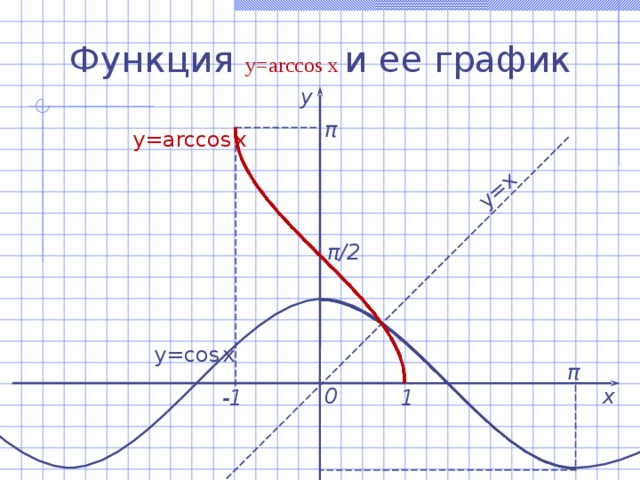
![Функция y=arccos x и ее свойства Если |а| ≤ 1 , то arccos а – это такое число из отрезка [ 0 ; π ] , косинус которого равен а . Если |а| ≤ 1 , то arccos а = t cos (arccos a) = a arccos (-a) = π – arccos a , где 0 ≤ а ≤ 1 cos t = а , 0 ≤ t ≤ π ;](https://fsd.kopilkaurokov.ru/up/html/2017/10/06/k_59d75c1c3e195/img_user_file_59d75c1cb3536_5.jpg)