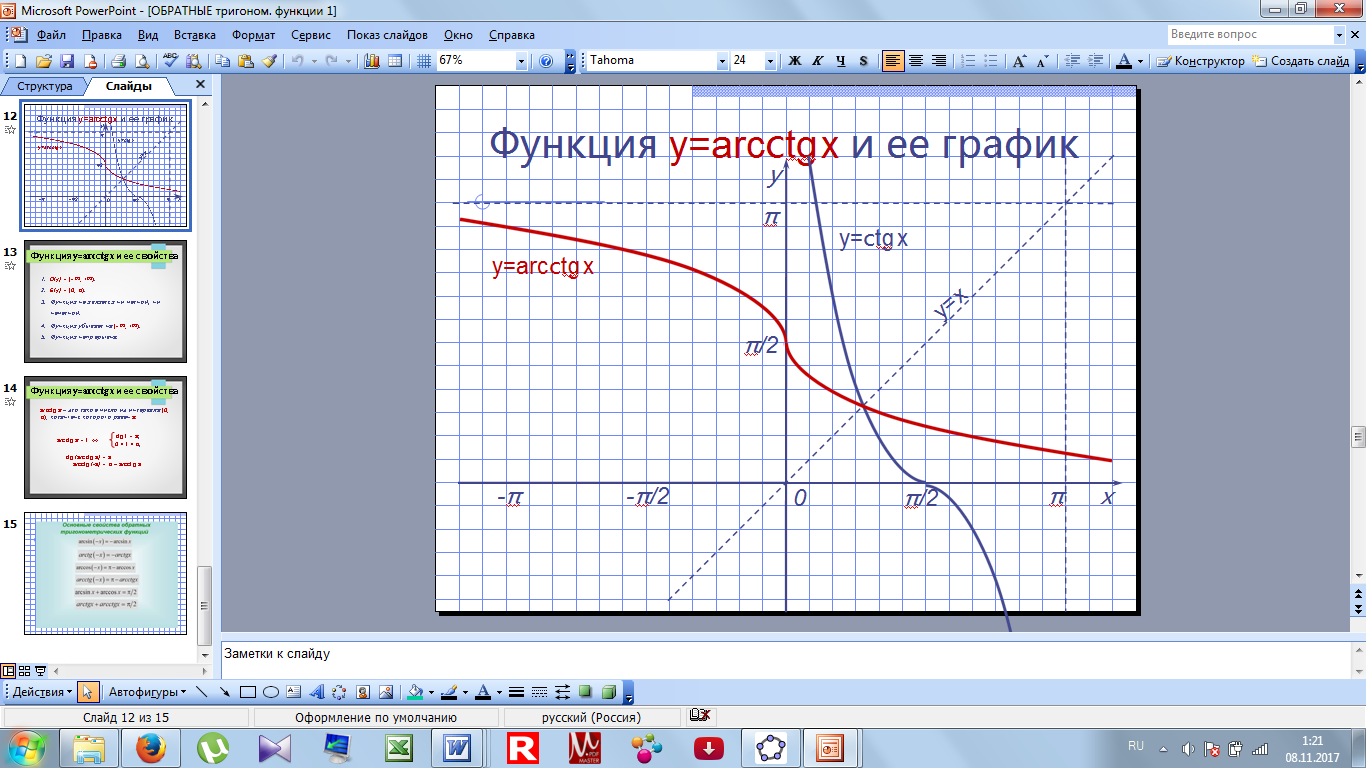
Темы "Тригонометрические функции" и "Обратные тригонометрические функции" на уроках математики в старших классах – одни из самых сложных тем. Целью данного урока является систематизация знаний о тригонометрических функциях, о взаимообратных функциях, их свойствах и графиках, а также формирование знаний обучающихся об обратных тригонометрических функциях и их свойствах, построение графиков этих функций, показать связь с тригонометрическими функциями; формирование навыков нахождения значений обратных тригонометрических функций
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Обратные тригонометрические функции
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Обратные тригонометрические функции»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
2020 руб.
2880 руб.
1900 руб.
2710 руб.
2020 руб.
2880 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
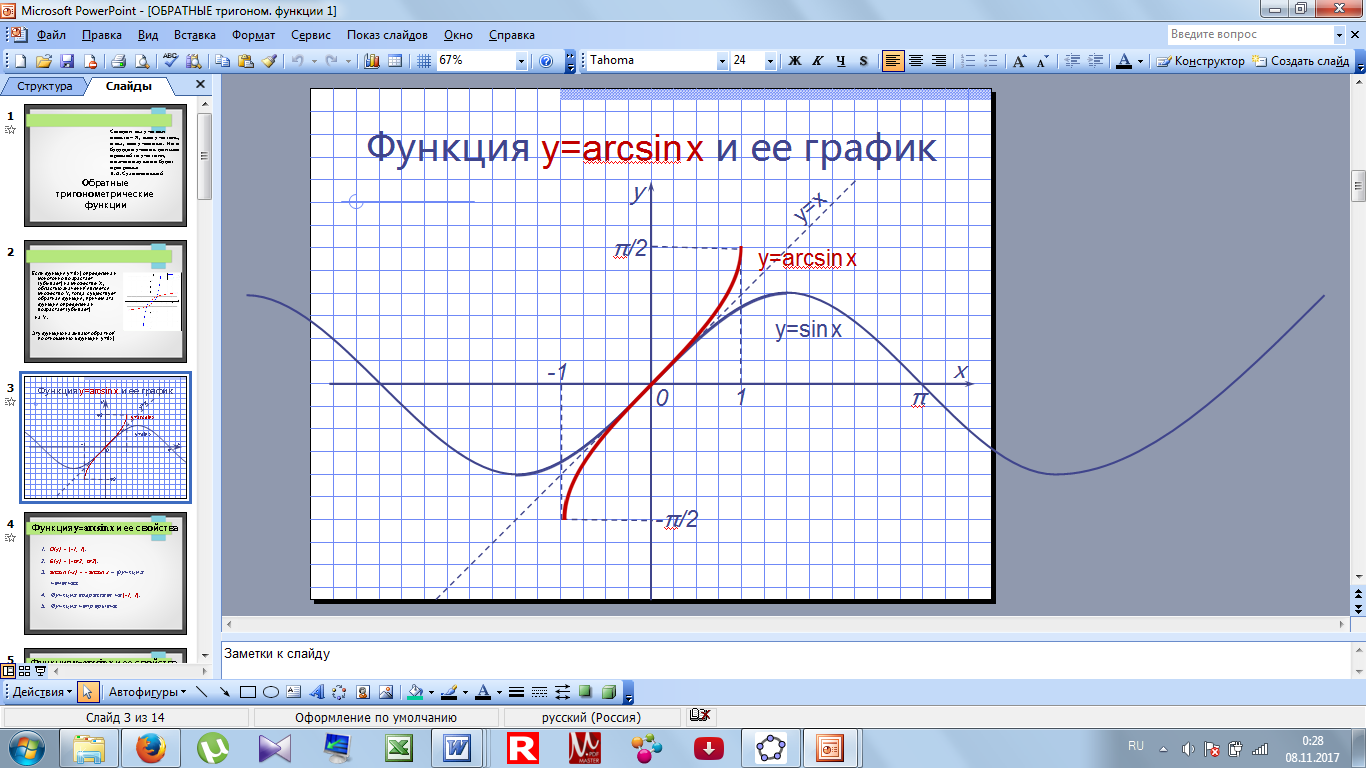 = arcsinx и по графику перечислить свойства. Построим график у = sinx на отрезке [-π/2; π/2]. Построим прямую у = х. Отобразим построенный график относительно этой прямой.
= arcsinx и по графику перечислить свойства. Построим график у = sinx на отрезке [-π/2; π/2]. Построим прямую у = х. Отобразим построенный график относительно этой прямой.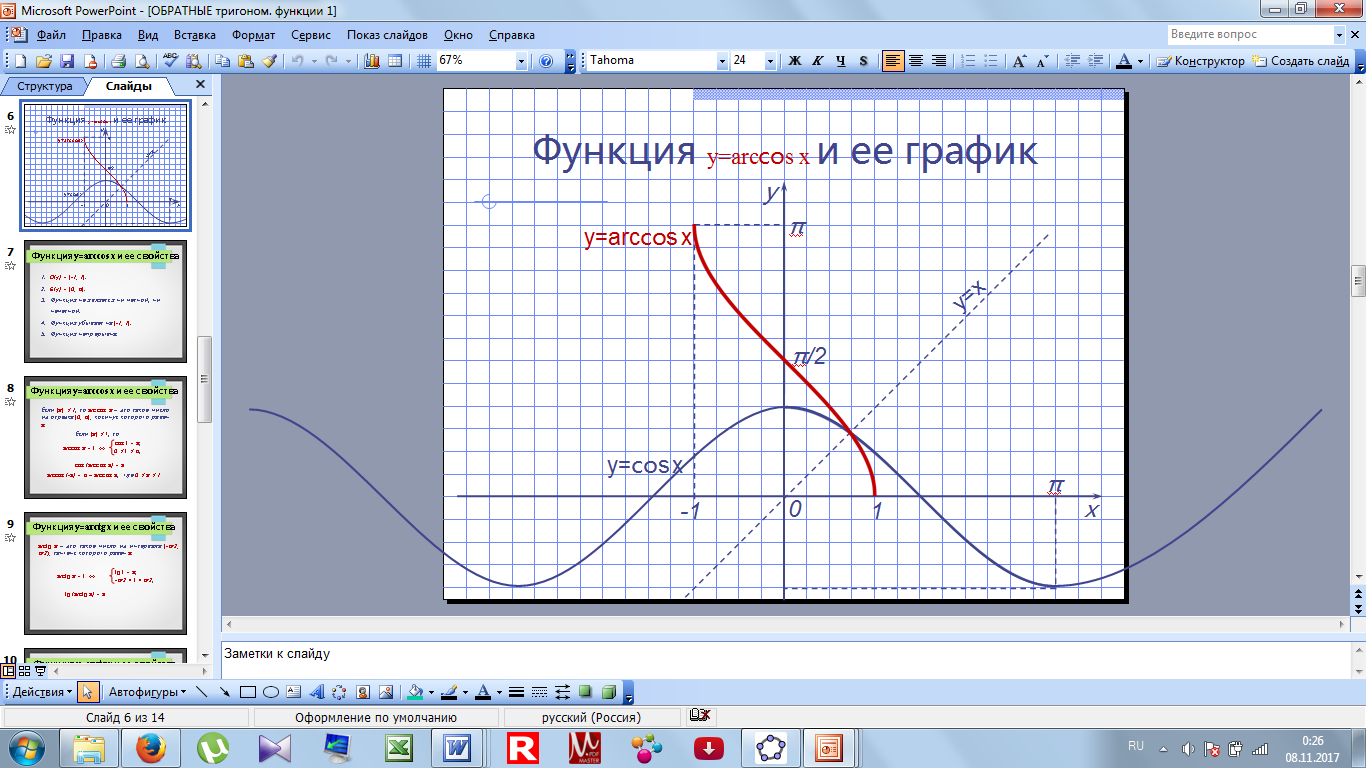
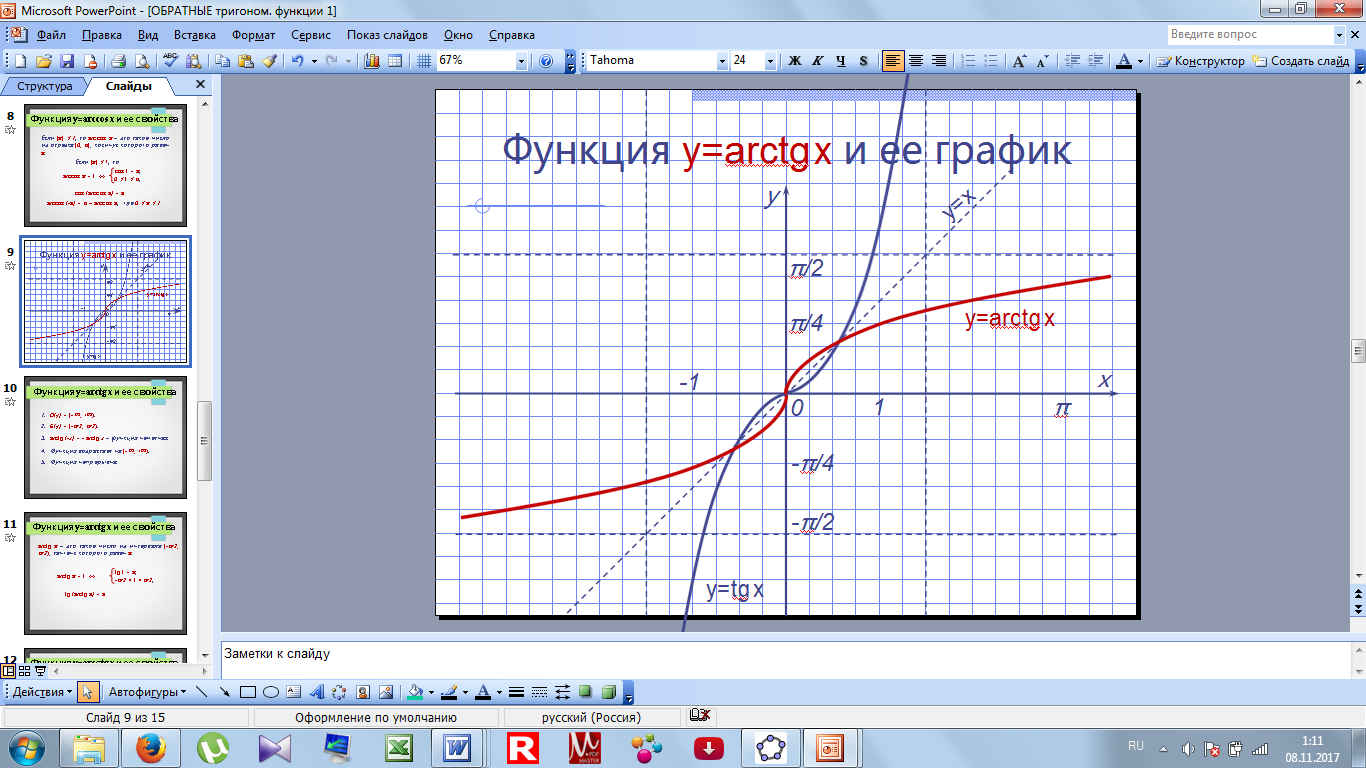 ункция непрерывна.
ункция непрерывна.