Тема нашего урока «Шар».
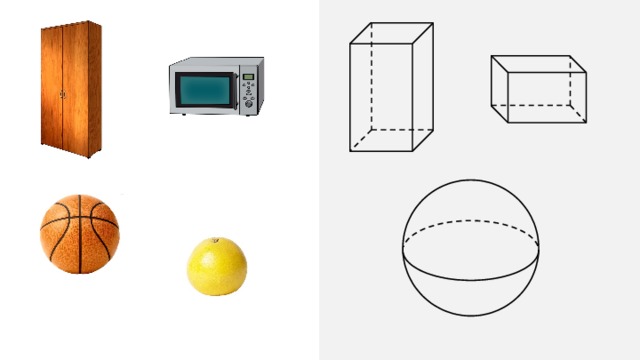
Нас окружают различные тела. Формы предметов окружающего мира очень разнообразны. Среди них встречаются так называемые «круглые тела». Хотелось бы сразу заметить, что на уроках математики не имеет значения цвет предмета и материал, из которого он изготовлен. Важна форма и размеры изучаемой фигуры. Особое место среди круглых тел занимает шар. Шар – это простейшее геометрическое тело. Форму, близкую к форме шара, имеют арбуз, апельсин, планеты … . Поверхность шара называют сферой. Можно сказать, что сфера – это как-бы оболочка или граница шара. Представление о сфере дают полые круглые предметы, например, мяч или пленка мыльного пузыря. Чтобы уяснить разницу между понятиями шар и сфера, посмотрите внимательно на экран. Перед вами изображены арбуз и кокос. Если мы разрежем арбуз, то внутри он будет полным. Арбуз – это пример шара. А если разрезать кокос, то вы заметите, что у кокоса внутри есть только оболочка. Кокос – это пример сферы.
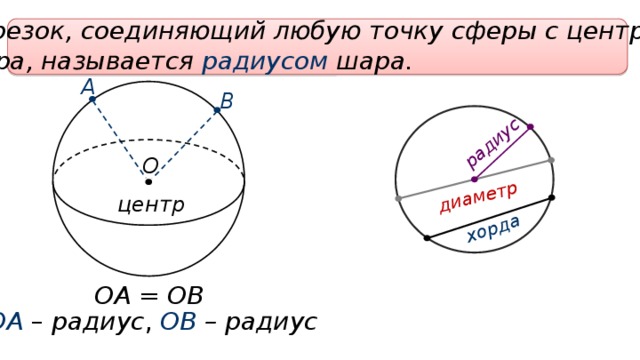
Шар и сфера, как круг и окружность, имеют центр, радиус и диаметр. Границей круга, как вам известно, является окружность, границей шара – сфера. Рассмотрим чертеж. Перед нами математическое изображение шара. Точка О – это центр шара. Все точки поверхности шара одинаково удалены от центра шара. Это означает, что если взять две любые точки на поверхности шара, например, А и В, и, соединить их с центром шара, то отрезки ОА и ОВ будут равны. Такие отрезки называют радиусами. Т.е. ОА – радиус шара и ОВ – тоже радиус шара.
Запишем определение:
Отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара. На рисунке отрезки ОА, ОВ, ОС и ОД являются радиусами.
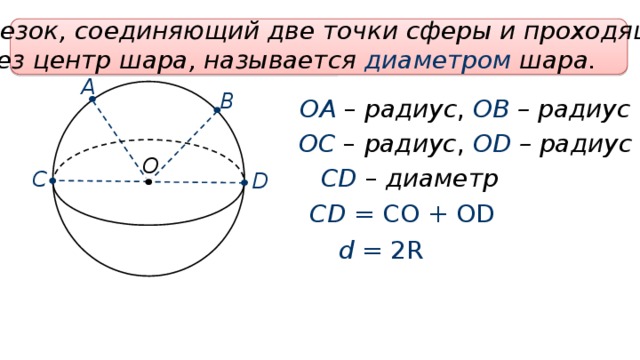
На рисунке также, смотрите, есть отрезок СД. Такой отрезок называют диаметром шара.
Запишем еще одно определение:
Отрезок, соединяющий две точки сферы и проходящий через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам.
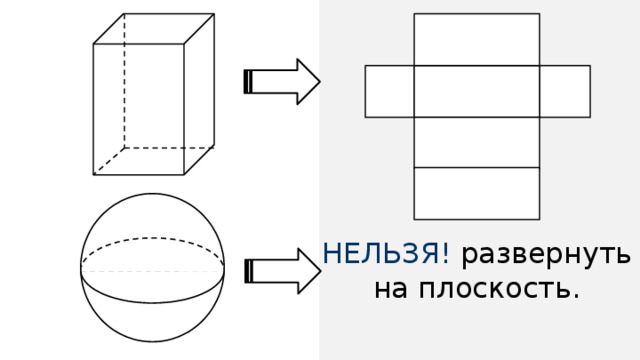
Еще в пятом классе вы познакомились с таким геометрическим телом, как прямоугольный параллелепипед, или призма. Вы знаете, что поверхность прямоугольного параллелепипеда можно развернуть на плоскость. А вот особенностью сферы является, то, что ее нельзя! развернуть на плоскость.
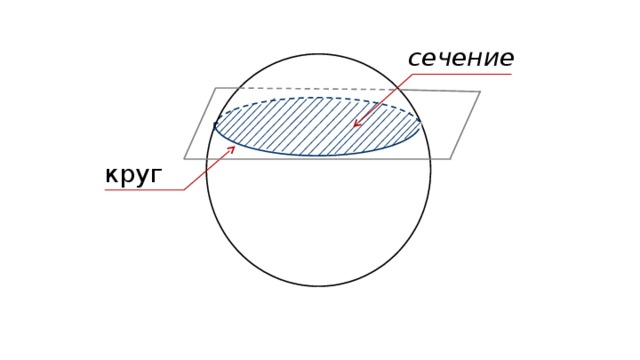
Если шар разрезать, то фигура, образованная на срезе, есть круг. Сам же срез называют сечением.
Решим задачу: чтобы измерить радиус футбольного мяча, Никита обмотал мяч по центру ниткой. Затем измерил ее. Длина нитки равна 59,66 см. Определите радиус футбольного мяча.
Решение: для того чтобы вычислить радиус футбольного мяча нам понадобится формула длины окружности. Длина нитки, которую мерил Никита, как раз таки и есть длина окружности. Выразим из формулы длины окружности радиус и подставим известные нам данные. За число пи возьмем число 3,14. Тогда радиус равен 59,66 разделить на 2 умноженное на 3,14. Посчитаем. Получаем, что радиус футбольного мяча равен 9,5 см.
Повторим главное:
Шар – это простейшее геометрическое тело.
Поверхность шара называют сферой.
Сферу нельзя! развернуть на плоскость.
Все точки поверхности шара одинаково удалены от центра шара.
Отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара.
Отрезок, соединяющий две точки сферы и проходящий через центр шара, называется диаметром шара.