Обобщающий урок
по теме
«Решение неравенств второй степени »
Место занятия урока в структуре образовательного процесса: урок по учебному плану по программе; учебник «Алгебра -9»под редакцией Теляковского.
Тема урока по учебному плану: Решение неравенств второй степени.
Форма урока: обобщающий урок
Класс: 9
Цель урока:
1.Систематизация, обобщение знаний учащихся; проверка уровня усвоения темы;
2. Формирование навыков самообразования, самоорганизации, работы в парах, умения анализировать, сравнивать, обобщать, делать выводы, развитие логического мышления.
3.Воспитание самостоятельности учащихся, умения выслушивать других и умения общаться в группах, повышения интереса к предмету.
Оборудование: «ромашка» с неравенствами (см. задание), компьютер, учебники.
Тип урока: Урок комплексного применения ЗУН учащихся:
Обобщение и систематизация знаний и способов деятельности.
Применение обобщенных ЗУН в новых условиях.
Контроль и самоконтроль знаний, умений и навыков.
.План проведения занятия:
Сообщение темы и цели урока.
Устная работа. Презентация.
Проверка домашнего задания (Найди ошибку)
Выполнение заданий
Самостоятельная работа.
Итог занятия
Ход урока
Устная работа
1. Игра «Ромашка». (На доске прикреплена ромашка, на лепестках которой с обратной стороны написаны разные неравенства. Нужно определить, какие неравенства являются квадратными.)
1) х2 + 4х-83) х3-14) х2 - Зх + 5 0;
5) х3 + х - 2 6) 5х-6 0; 7) х2 - 4 . Ответ: 1, 4, 7.
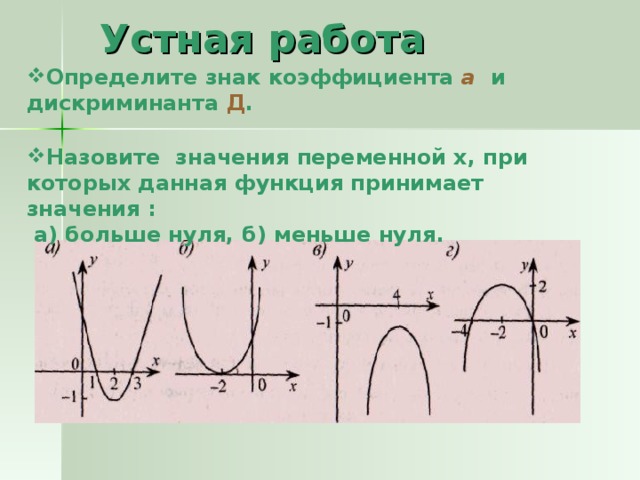
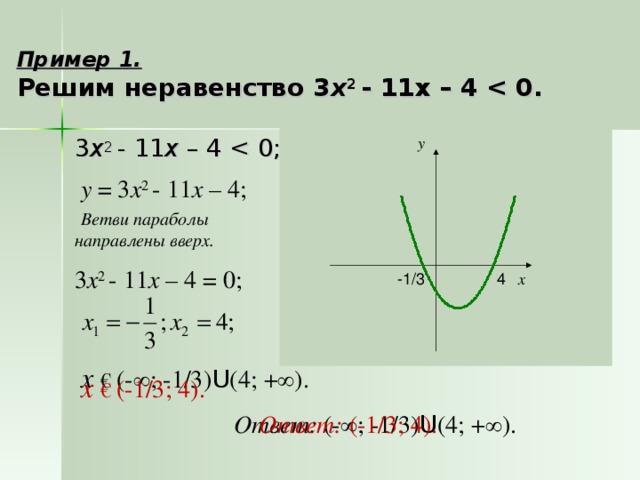
2. На рисунках изображен график функции у = ах2 + вх + с.
Определите знак коэффициента а и дискриминанта Д.
Назовите значения переменной х, при которых данная функция принимает значения:
а) больше нуля, б) меньше нуля;
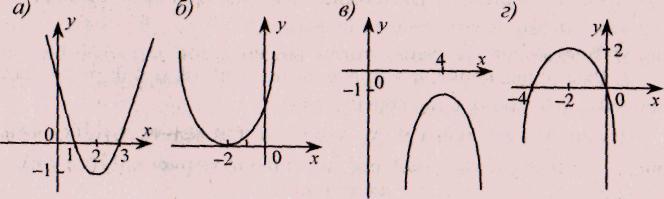
Ответы: рис. а: а6, Д0; рис. б; а0, Д= 0;
рис. в: а 0, Дрис. г: а 0.
Вопрос учащимся: К чему сводится решение задания при нахождении промежутков, при которых у 0? (Ответ: к решению квадратных неравенств)
Рассказать алгоритм решения квадратных неравенств.
Работа с сильными уч-ся: (Проверка домашнего задания)
Уч-ся раздаются задания с готовым решением, но с ошибкой. Надо найти ошибку и показать правильное решение.
II. Выполнение заданий
Работа в парах:
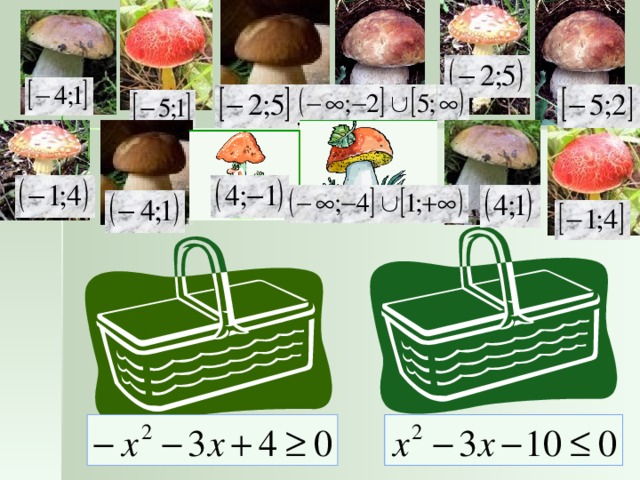
1. На доске изображен квадрат с числами, которые являются решениями неравенства х2 + 6х + 5 0. Но среди них попало число, которое таковым не является. Найдите это число.
| -6 | 4 | -9 | 0 |
| -10 | 2 | 6 | 3 |
| 1 | 7 | -2 | -8 |
| 8 | -7 | 9 | 5 |
Решение: х2 + 6х + 5 0.
Квадратное уравнение х2 + 6х + 5 = 0 имеет два различных корня: х1 = -1 и х2 = -5.
Самостоятельная работа.

Слайды





Выполнение заданий:
Практическая задача (Работа в парах):
Одна сторона сада прямоугольной формы на 7 м больше другой. Какой может быть меньшая сторона сада, если его площадь должна не превосходит 60 м2?
Решение: Пусть х м- меньшая сторона сада, тогда (х+7) м - большая сторона. По условию задачи получаем неравенство: 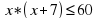 .
.
Решаем неравенство: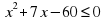 . D=72-4*1*(-60)=289. х1= -12, х2=5. х € [-12; 5]
. D=72-4*1*(-60)=289. х1= -12, х2=5. х € [-12; 5]
По условию задачи 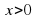 , поэтому меньшая сторона сада может принимать размеры (0;5]. Ответ: (0;5].
, поэтому меньшая сторона сада может принимать размеры (0;5]. Ответ: (0;5].
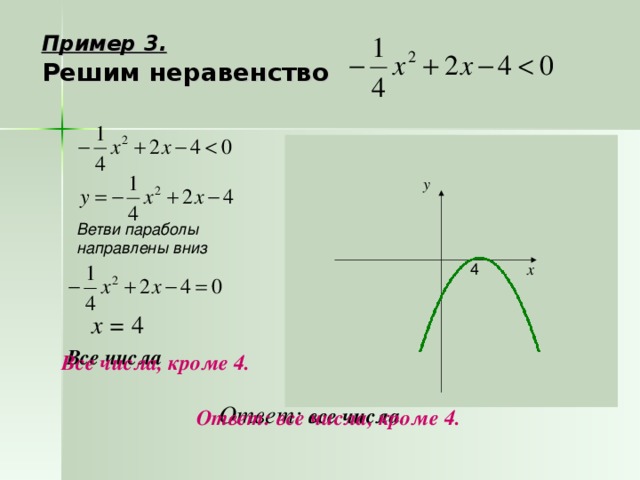
2. Дополнительное задание:
Найдите область определения функции 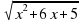
 Работа в парах:
Работа в парах:
Решение : х2+6х+5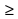 0 х2+6х+5=0 х1= -1, х2= -5.
0 х2+6х+5=0 х1= -1, х2= -5.
Ответ : 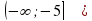
Самостоятельная работа
[-2; 5], (2; 5), [0; 2], [-1; 2), [3;5].
Ребята обмениваются Уч-ся обмениваются тетрадями для взаимопроверки.(Слайд № 7)
 Корзинки
Корзинки
1).
 2).
2).
С
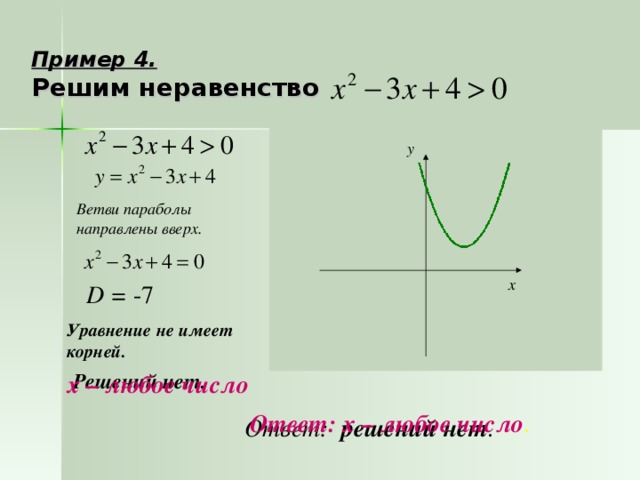
Самостоятельная работа (Слайд №12)
На доске «висят» «грибочки», которые следует собрать в две «корзины». Каждая
«корзинка» - определенное квадратное неравенство. «Грибочки» - числовые промежутки. Поэтому «грибочки» должны быть «помещены» только в свою корзину.


1). 2).
«Грибочки» «корзин»:
[-4;1] 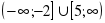
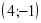
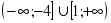
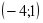
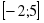
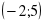
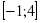
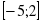
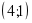
(-1;4) [-5;1]
 ,
,
Проверка самостоятельной работы. Уч-ся обмениваются тетрадями. Проверка (Слайды № 13, 14, 15).
Домашнее задание: п.14 №319; Придумать или найти творческое задание, где применяется решение квадратных неравенств
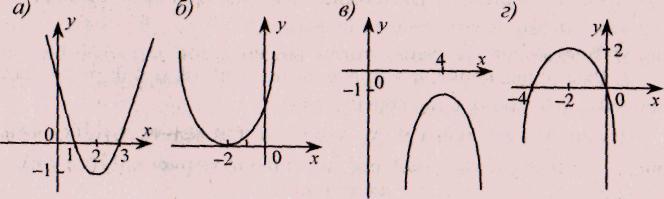

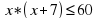 .
.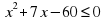 .
. 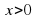 , поэтому меньшая сторона сада может принимать размеры (0;5]. Ответ: (0;5].
, поэтому меньшая сторона сада может принимать размеры (0;5]. Ответ: (0;5]. 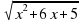
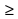 0 х2+6х+5=0 х1= -1, х2= -5.
0 х2+6х+5=0 х1= -1, х2= -5. 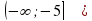



![Пример 2. Решим неравенство - 5 х 2 - 9х + 2 ≤ 0. - 5 x 2 - 9 x + 2 ≤ 0; y y = - 5 x 2 - 9 x + 2 ; Ветви параболы направлены вверх. Ветви параболы направлены вниз. - 5 x 2 + 9 x – 2 = 0; 1/5 -2 x x € [-2; 1/5] Ответ: [-2; 1/5] .](https://fsd.kopilkaurokov.ru/uploads/user_file_5451557de4f23/img_user_file_5451557de4f23_1_5.jpg)

 0 . Но среди них попало число, которое таковым не является. Найдите это число. -6 4 -10 2 1 -9 0 6 8 7 3 -7 -2 -8 9 5" width="640"
0 . Но среди них попало число, которое таковым не является. Найдите это число. -6 4 -10 2 1 -9 0 6 8 7 3 -7 -2 -8 9 5" width="640"


![Вариант 1. Решите неравенство - х 2 - 3х + 4 ≥ 0. на «3» на «4» - x 2 - 3 x + 4 ≥ 0; y y = - x 2 - 3 x + 4 ; График-парабола. Ветви параболы направлены вниз. - x 2 - 3 x + 4 = 0; 1 -4 x на «5» x € [- 4 ; 1] Ответ x € [- 4 ; 1] .](https://fsd.kopilkaurokov.ru/uploads/user_file_5451557de4f23/img_user_file_5451557de4f23_1_13.jpg)
![Вариант 2. Решим неравенство х 2 - 3х -10 ≤ 0. на « 4 » на «3» y x 2 - 3 x -10 ≤ 0; y = x 2 - 3 x -10 ; График-парабола. Ветви параболы направлены вверх. 5 -2 x x 2 - 3 x -10 = 0; на « 5 » x € [-2; 5] Ответ: x € [ -2; 5] .](https://fsd.kopilkaurokov.ru/uploads/user_file_5451557de4f23/img_user_file_5451557de4f23_1_14.jpg)


















