Урок алгебры в 9 классе с использованием ИКТ/
Тема урока: «Решение неравенств второй степени с одной переменной».
Тип урока: урок с использование ИКТ (информационно – коммуникационных технологий).
Цели урока:
- Актуализировать знания, необходимые для изучения данной темы;
- Развивать умения и отработать навыки применения изученной темы на практике; развивать логическое мышление;
Оборудование: компьютер, проектор, презентация «Решение неравенств второй степени с одной переменной».
Ход урока.
1.Организационный момент.
Сформулировать тему и цели урока. Записать число и тему урока в тетрадь.
(Запустить презентацию «Решение неравенств второй степени с одной переменной»).
2.Устная работа.
(беседа)
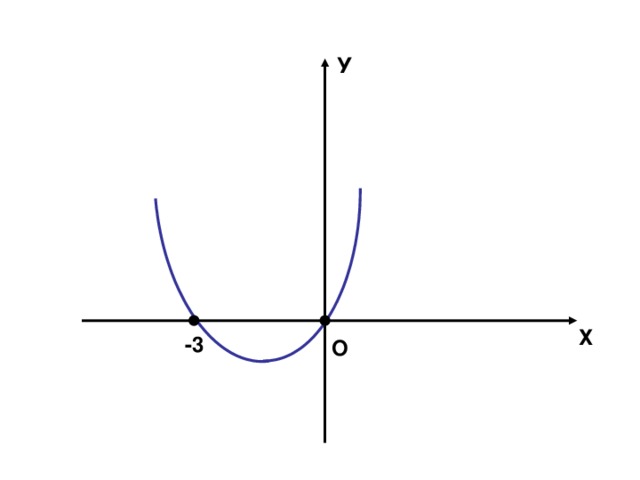
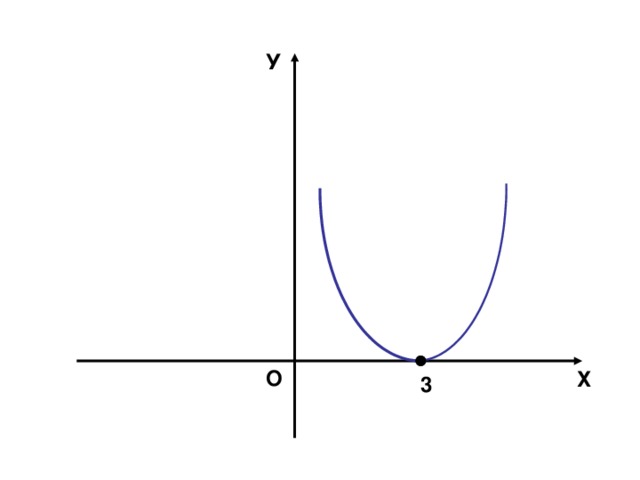
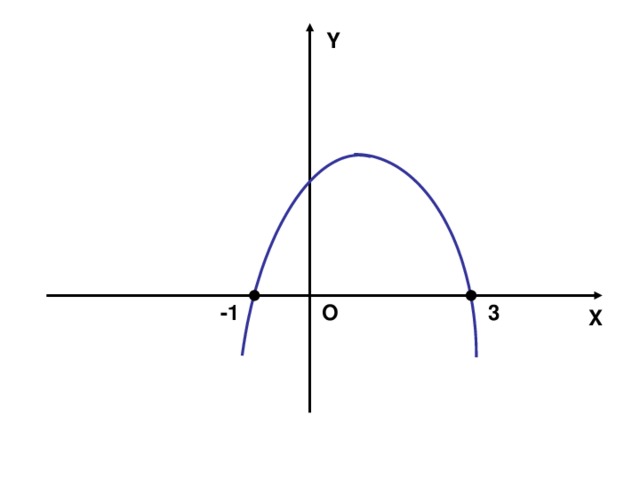
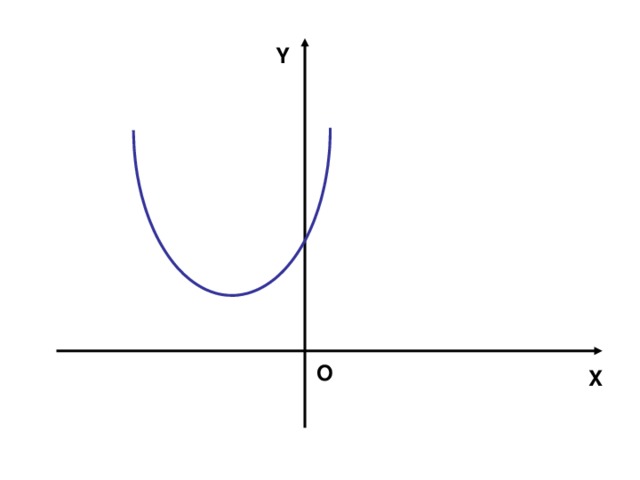
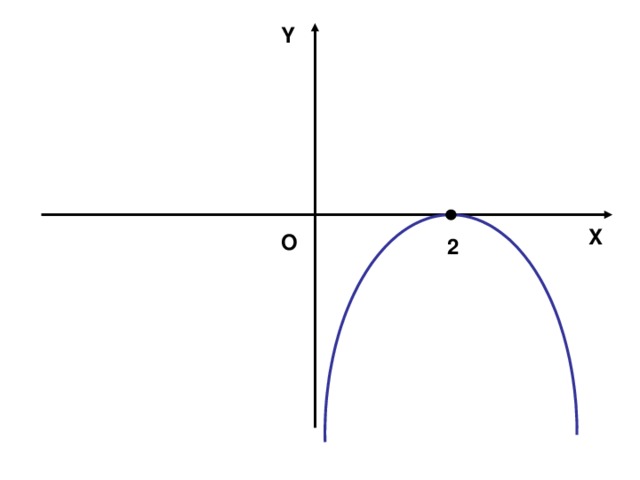
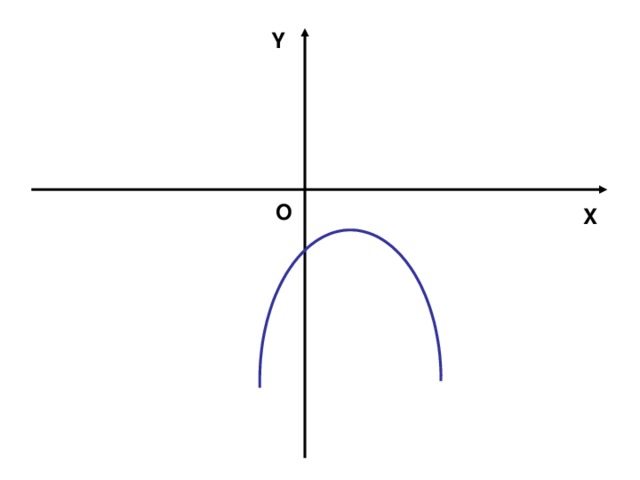
(Слайд № 2). 1. Ребята, какая функция изображена на слайде?
2. Чему равен дискриминант, в данном случае?
3. Чему равен коэффициент а? Почему?
4. При каких значениях, функция принимает положительные значения?
5. При каких значениях, принимает отрицательные значения?
Аналогично разбираем слайд № 3-7.
Просмотрев данные слайды, мы с вами можем сделать следующие выводы, что ….(квадратичная функция принимает положительные значения, на тех участках, где она расположена выше оси х. А отрицательные значения, там, где квадратичная функция расположена ниже оси х).
3.Объяснение нового материала.
(Слайд №8). Итак, неравенства вида ax+bx+c>0 и ax+bx+c<0, где x – переменная, a, b и c – некоторые числа, причем a не нулевое, называется неравенством второй степени с одной переменной. (Записать в тетрадь).
Решить неравенство, значит найти промежутки, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения. (Записать в тетрадь).
Давайте посмотрим с вами следующий слайд (Слайд №9).
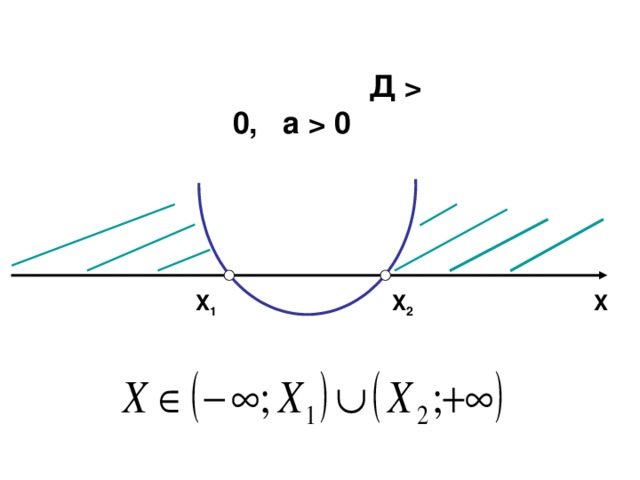
Решение какого неравенства изображено на этом слайде?
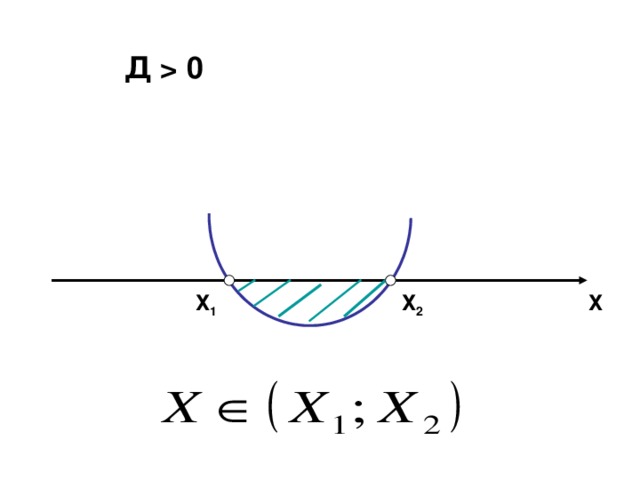
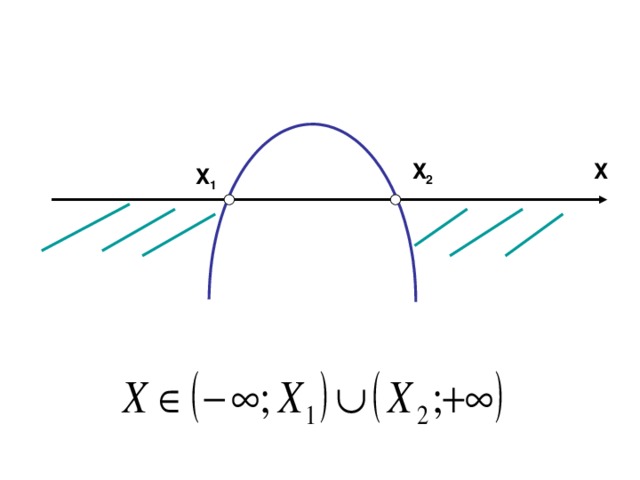
(Слайд №10). На данном слайде чему равно а, почему? Решение какого неравенства изображено на этом слайде? Аналогично рассматриваются и разбираются слайды №11-15.
Давайте попробуем с вами разработать этапы алгоритма, при помощи которого, можно решить неравенство второй степени с одной переменной. (Выслушать предложения ребят и вместе выстроить алгоритм решения). (Слайд № 16) (Алгоритм остается на экран).
Давайте решим с вами следующие неравенство. (Решение записать на доске, с поэтапным объяснением)
Квадратичная функция, графиком которой является парабола, ветви направлены вверх.
Найдем нули функции
Парабола пересекает ось х в двух точках. Нарисуем схематично параболу, проходящую через эти точки, и выпишем ответ.
4.Решение задач.
№304 (а), №305 (б).
5.Самостоятельная работа, с дальнейшей самопроверкой (7 минут).
(Слайд № 17).
6.Итоги урока.
(Слайд № 18).
7.Задание на дом.
Пункт 14, №304 (д, е), №305 (а).
(Презентация в к данному уроку в архиве).
Просмотр содержимого документа
«урок алгебры с использованием ИКТ. Моисеева Е. П., гимназия №9»
Урок алгебры в 9 классе с использованием ИКТ.
Тема урока: «Решение неравенств второй степени с одной переменной».
Тип урока: урок с использование ИКТ (информационно – коммуникационных технологий).
Цели урока:
Актуализировать знания, необходимые для изучения данной темы;
Развивать умения и отработать навыки применения изученной темы на практике; развивать логическое мышление;
Оборудование: компьютер, проектор, презентация «Решение неравенств второй степени с одной переменной».
Ход урока.
Организационный момент.
Сформулировать тему и цели урока. Записать число и тему урока в тетрадь.
(Запустить презентацию «Решение неравенств второй степени с одной переменной»).
Устная работа.
(беседа)
(Слайд № 2). 1. Ребята, какая функция изображена на слайде?
2. Чему равен дискриминант, в данном случае?
3. Чему равен коэффициент а? Почему?
4. При каких значениях 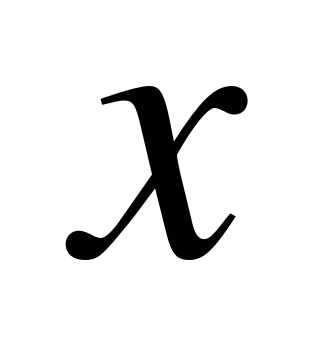 , функция принимает положительные значения?
, функция принимает положительные значения?
5. При каких значениях 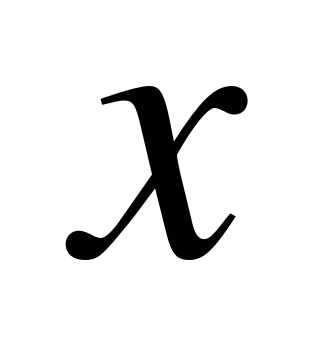 , принимает отрицательные значения?
, принимает отрицательные значения?
Аналогично разбираем слайд № 3-7.
Просмотрев данные слайды, мы с вами можем сделать следующие выводы, что …..(квадратичная функция принимает положительные значения, на тех участках, где она расположена выше оси х. А отрицательные значения, там, где квадратичная функция расположена ниже оси х).
Объяснение нового материала.
(Слайд №8).
Итак, неравенства вида ax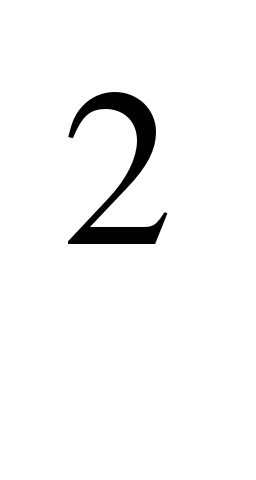 +bx+c0 и ax
+bx+c0 и ax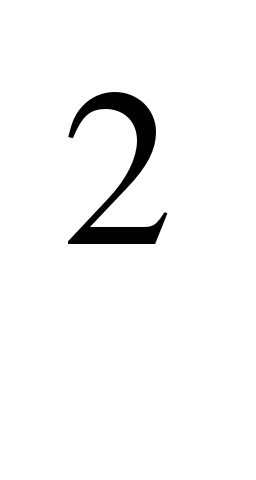 +bx+cx – переменная, a, b и c – некоторые числа, причем a не нулевое, называется неравенством второй степени с одной переменной. (Записать в тетрадь).
+bx+cx – переменная, a, b и c – некоторые числа, причем a не нулевое, называется неравенством второй степени с одной переменной. (Записать в тетрадь).
Решить неравенство, значит найти промежутки, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения. (Записать в тетрадь).
Давайте посмотрим с вами следующий слайд (Слайд №9).
Решение какого неравенства изображено на этом слайде?
(Слайд №10). На данном слайде чему равно а, почему? Решение какого неравенства изображено на этом слайде? Аналогично рассматриваются и разбираются слайды №11-15.
Давайте попробуем с вами разработать этапы алгоритма, при помощи которого, можно решить неравенство второй степени с одной переменной. (Выслушать предложения ребят и вместе выстроить алгоритм решения). (Слайд № 16) (Алгоритм остается на экран).
Давайте решим с вами следующие неравенство. (Решение записать на доске, с поэтапным объяснением)
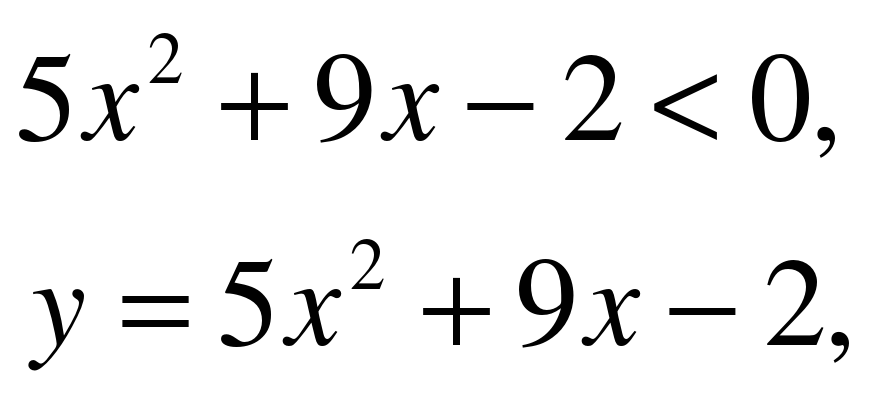
Квадратичная функция, графиком которой является парабола , ветви направлены вверх.
Найдем нули функции 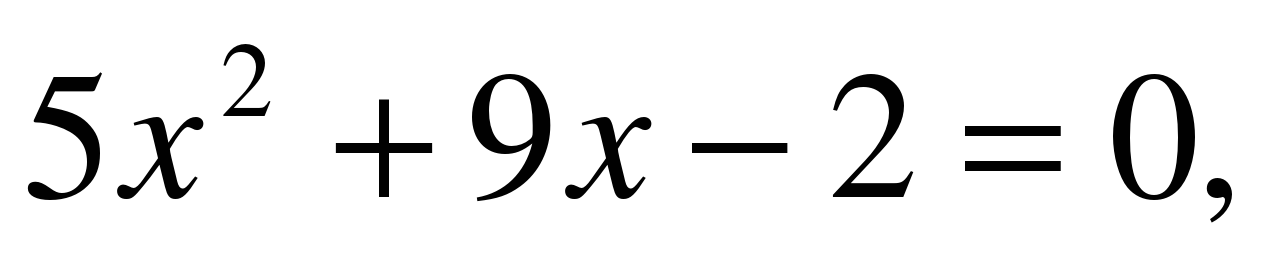
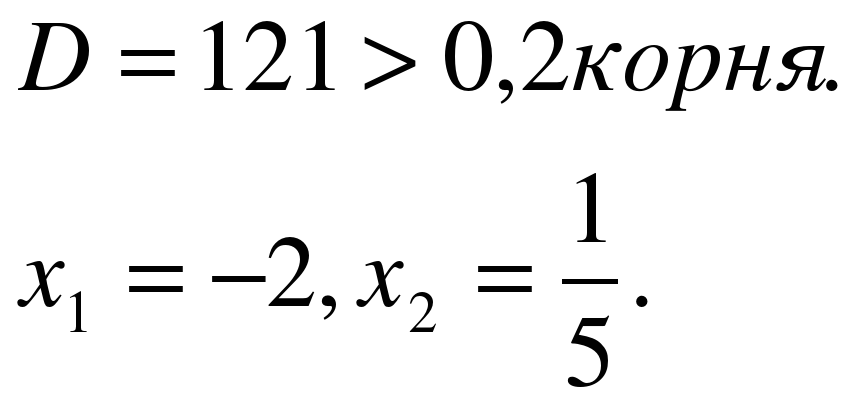
Парабола пересекает ось х в двух точках. Нарисуем схематично параболу, проходящую через эти точки, и выпишем ответ.

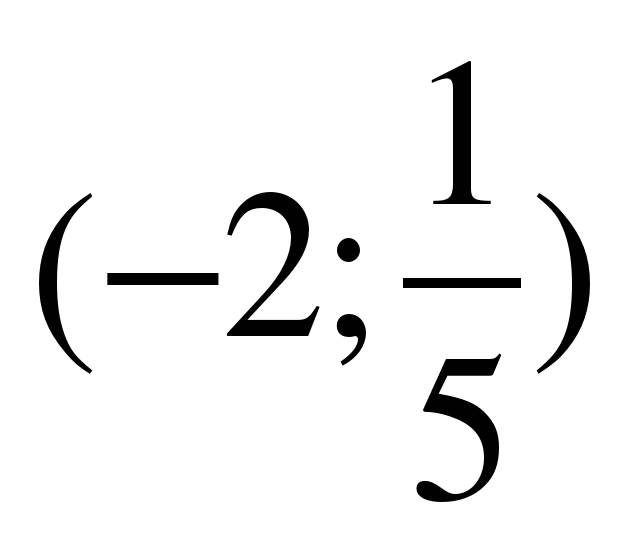
Решение задач.
№304 (а), №305 (б).
Самостоятельная работа, с дальнейшей самопроверкой (7 минут).
(Слайд № 17).
Итоги урока.
(Слайд № 18).
Задание на дом.
Пункт 14, №304 (д, е), №305 (а).
Просмотр содержимого презентации
«решение неравенств второй степени с одной переменной»
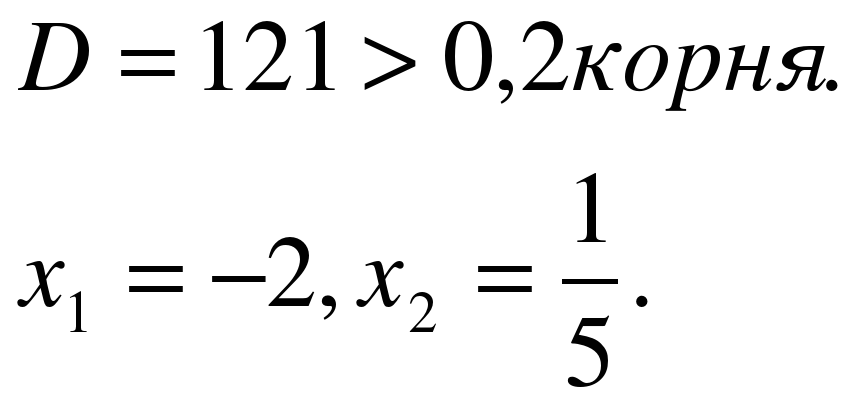


 0 и ax 2 +bx+c , где x – переменная, a, b и c – некоторые числа, причем a не нулевое, называется неравенством второй степени с одной переменной. Решить неравенство, значит найти промежутки в которых соответствующая квадратичная функция принимает положительные или отрицательные значения." width="640"
0 и ax 2 +bx+c , где x – переменная, a, b и c – некоторые числа, причем a не нулевое, называется неравенством второй степени с одной переменной. Решить неравенство, значит найти промежутки в которых соответствующая квадратичная функция принимает положительные или отрицательные значения." width="640"
 0, а 0 X 1 X 2 X" width="640"
0, а 0 X 1 X 2 X" width="640"
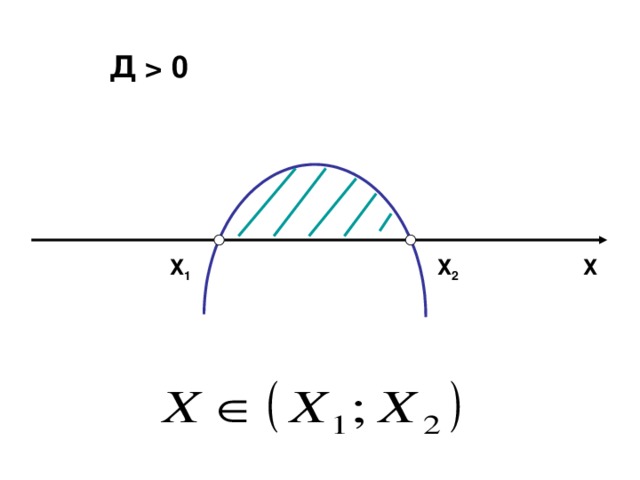 0 Х Х 1 Х 2" width="640"
0 Х Х 1 Х 2" width="640"
 0 Х Х 1 Х 2" width="640"
0 Х Х 1 Х 2" width="640"
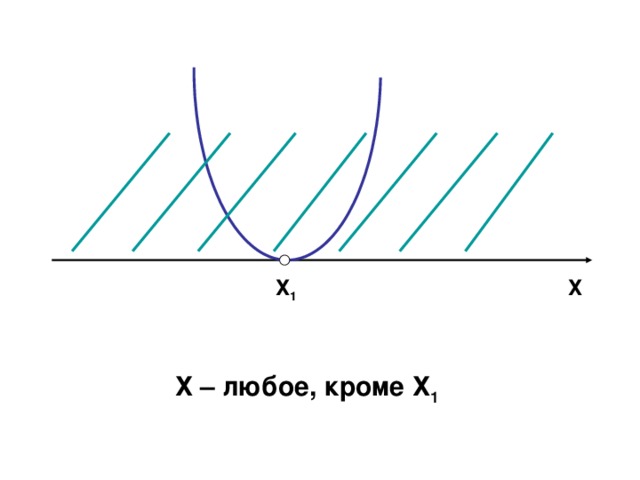
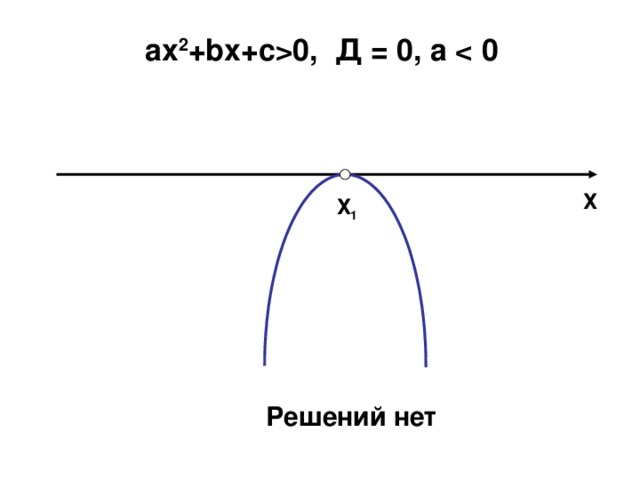 0 , Д = 0, а 0 Х Х 1 Решений нет" width="640"
0 , Д = 0, а 0 Х Х 1 Решений нет" width="640"
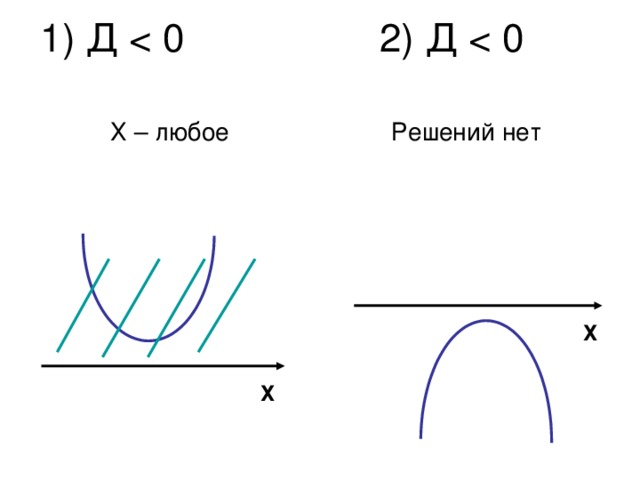
 0 и ax 2 +bx+c" width="640"
0 и ax 2 +bx+c" width="640"
 0 Вариант 2 а) 4х 2 +11х-3 0 б) х 2 -10х+21" width="640"
0 Вариант 2 а) 4х 2 +11х-3 0 б) х 2 -10х+21" width="640"
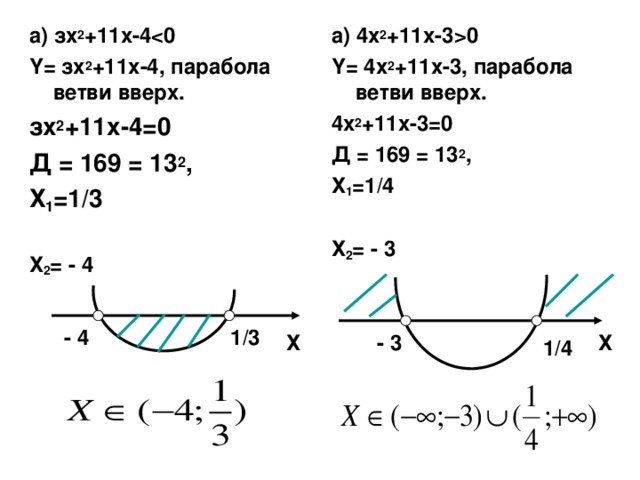 0 Y= 4х 2 +11х-3, парабола ветви вверх. 4х 2 +11х-3=0 Д = 169 = 13 2 , Х 1 =1 /4 Х 2 = - 3 - 4 1/3 Х - 3 Х 1 /4" width="640"
0 Y= 4х 2 +11х-3, парабола ветви вверх. 4х 2 +11х-3=0 Д = 169 = 13 2 , Х 1 =1 /4 Х 2 = - 3 - 4 1/3 Х - 3 Х 1 /4" width="640"
















