Цели урока:
Образовательная:
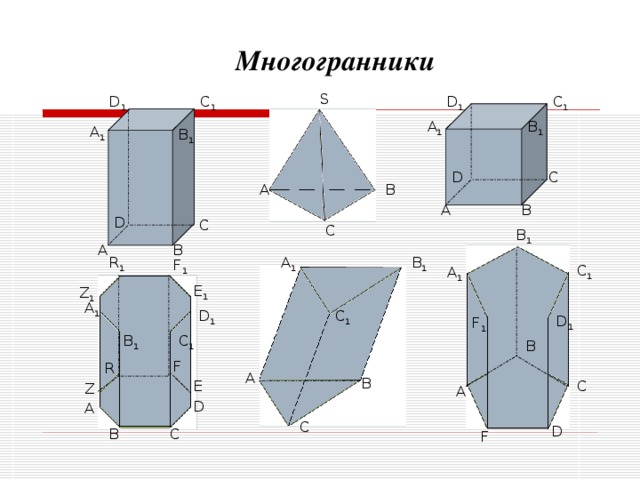
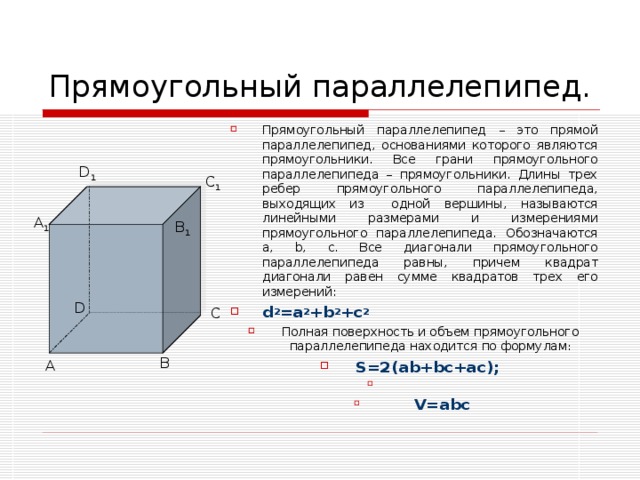
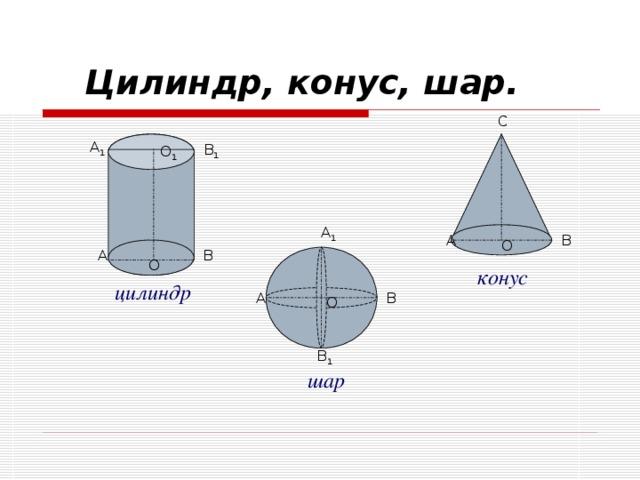
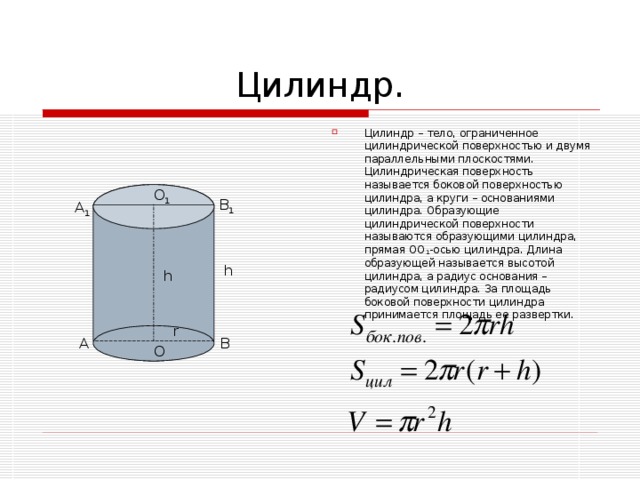
- Знать формулы для вычисления объёмов многогранников и тел вращения;
- Уметь применять полученные знания для решения задач;
- Подготовка к единому национальному тестированию
- учащиеся должны уметь работать с презентацией и тестами на компьютерах
Развивающая:
- логическое мышление;
- умение самостоятельно добиваться знаний;
- развивать навыки работы на компьютере;
Воспитывающая:
- воспитывать умения слушать и слышать;
- культуре речи;
- умственное воспитание;
- внимание и усидчивости;
- воспитание интереса и положительного отношения к учению;
- воспитывать интерес к предмету математика и информатика через создание ситуации успеха.
Тип урока: интегрированный урок.
Средства обучения:
для ученика:
1.раздаточный материал
2.ТСО ( компьютер)
для учителя:
1.наглядные пособия;
2.кадоскоп;
3.компьютер;
4.таблица
Формы обучения:
- индивидуальная
- общеклассная
- интерактивная ( ученик – компьютер)
Методы обучения:
- словесно-наглядный
- практический
- репродуктивный
- индуктивный
- частично – поисковый
- творческий