Презентация к уроку по теме:"Аксиомы стереометрии"

Тема: «Построение сечений многогранников»

Цели и задачи урока:

• Закрепление навыков построения сечений на примере пирамиды.

• Обобщение учебного материала по теме через формирование умения применять приёмы построения сечений в новой ситуации (сечение параллелепипеда).

• Формирование навыков исследовательской работы; в том числе умения синтезировать и анализировать, обобщать, выделять главное.

• Формирование специальных умений и навыков, в том числе навыков использования математического языка.

• Развитие технического, логического, образно-пространственного мышления учащихся.

• Воспитание культуры графического труда.

Материалы и оборудование:

Для обучающихся:

• Рабочая тетрадь.

• Ручка, карандаш, резинка.

• Раздаточный материал.

Карточки для индивидуальной работы. Приложение 1

Для преподавателя:

• Слайдовая презентация PowerPoint «Сечение многогранников плоскостью». Приложение 2.

• Проектор

• Ноутбук с презентационными и иными материалами к уроку.

Педагогические средства для решения поставленных задач:

1. Тип урока: закрепление полученных знаний.

2. Материал, изучаемый на уроке, представлен, развернуто, введена научная терминология.

3. Для повышения эффективности урока и подачи нового материала в более доступной динамичной форме, использованы слайдовая презентация

4. Для изложения нового материала применены приемы фронтальной работы со слайдом, задана самостоятельная проблемная работа по построению сечений многогранников, стимулирующая саморазвитие обучающихся и мотивирующая их на изучение темы «Сечения многогранников».

Ход урока:

1. Организационный момент.

2. Проверка домашнего задания (фронтально, ответы на доске)

3. Актуализация прежних знаний (повторение аксиом планиметрии, стереометрии и теорем о существовании плоскости), методы построения сечений.

(слайды №1,2,3)

Перед обучащимися ставится задача, в ходе решения которых повторяются основные аксиомы и теоремы. Осуществляется пошаговая проверка построения сечения.

На данном этапе отрабатывается умение аргументировать свое решение.

4. Закрепление навыка построения сечений и запись алгоритма (сл.№4)

Двое обучающихся выполняют данную задачу у доски с последующей проверкой с помощью презентации. Этап позволяет проконтролировать сформированность навыков грамотной математической записи.

5. Обобщение полученных знаний при построении сечений куба (слайд №7).

Ученики выполняют задание самостоятельно в тетради с последующей самопроверкой (материалы к уроку). В случае затруднения при работе обучающиеся могут использовать подсказку в презентации «Для самостоятельного изучения» Приложение 3.

6. Рассмотрим задачу:

Дан куб ABCDA₁B₁C₁D₁. Через точки С, D₁ и середину ребра АА₁ проведена плоскость. Найдите площадь сечения, если ребро куба равно 4.

7. Обсуждение и проверка полученного результата. ( слайд №8)

8. Подведение итогов урока и домашнее задание с комментариями к нему. (слайды №№26,27,28). Приложение 2

Домашняя работа

• на «3» - построить сечение на бумажном носителе без описания;

• на «4» - построить сечение с пошаговым описанием построения (см.слайд 4)

• на «5» – построить сечение с полным обоснованием (пошаговым описанием построения и ссылками на аксиомы и теоремы).

Если теорему так и не смогли доказать, она становится аксиомой.

Евклид

Аксиомы стереометрии.

Геометрия. 1 курс.

Урок № 1.

Геометрия

Планиметрия

Стереометрия

stereos - телесный, твердый, объемный, пространственный

metreo - измерять

Стереометрия.

Раздел геометрии, в котором

изучаются свойства фигур

в пространстве.

Основные фигуры в пространстве:

Плоскость.

Прямая.

Точка.

А

а

Обозначение основных

фигур в пространстве:

точка

прямая

плоскость

A, B, C, …

a, b, c, …

или

AВ, BС, CD, …

Геометрические тела:

Куб.

Октаэдр.

Параллелепипед.

Тетраэдр.

Геометрические тела:

Цилиндр.

Конус.

Шар.

Геометрические понятия.

• Плоскость – грань
• Прямая – ребро
• Точка – вершина

вершина

грань

ребро

Аксиома

(от греч. axíõma – принятие положения)

исходное положение научной теории, принимаемое без доказательства

Аксиомы стереометрии.

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

В

А

С



Аксиомы стереометрии.

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

В

А



Аксиомы стереометрии.



А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей .



Аксиомы стереометрии описывают:

А3.

А1.

А2.

Взаимное расположение плоскостей

Взаимное расположение прямой и плоскости

Способ задания плоскости



В

А

А

В







С

Взаимное расположение прямой и плоскости.

Прямая лежит в плоскости.

Прямая пересекает плоскость.

Прямая не пересекает плоскость.

а

а

М





g

а

а ⊄ 

а  

а ∩  = М

Нет общих точек.

Единственная общая точка.

Множество общих точек.

Прочитайте чертеж

С

A

Прочитайте чертеж

c

b

B

a

Прочитайте чертеж

Пользуясь данным рисунком, назовите:

а) две плоскости, содержащие прямую DE , прямую EF

б) прямую, по которой пересекаются плоскости

DEF и SBC ; плоскости FDE и SAC ;

в) две плоскости, которые пересекает прямая SB ; прямая AC .

S

E

D

С

А

F

В

Пользуясь данным рисунком, назовите:

S

а) Две плоскости, cодержащие

E

прямую DE .

D

б) Прямую по которой пересекаются плоскости

АЕF и SBC .

А

С

F

в) Плоскость, которую пересекает прямая SB .

В

Пользуясь данным рисунком, назовите:

S

а) Две плоскости,

cодержащие прямую EF .

E

б) Прямую по которой

пересекаются плоскости

BDЕ и SAC .

D

А

С

F

в) Плоскость, которую

пересекает прямая AC .

В

Домашнее задание:

• Выучить аксиомы.

3) № 1 (в, г); 2(в, г); 6.

2) П. 2-3

стр. 4 – 6.

Комментарий к задаче № 6:

2 случай: точки лежат

в одной плоскости.

1 случай: точки лежат

на одной прямой.

В

С

А

В

А

С

Удачи!

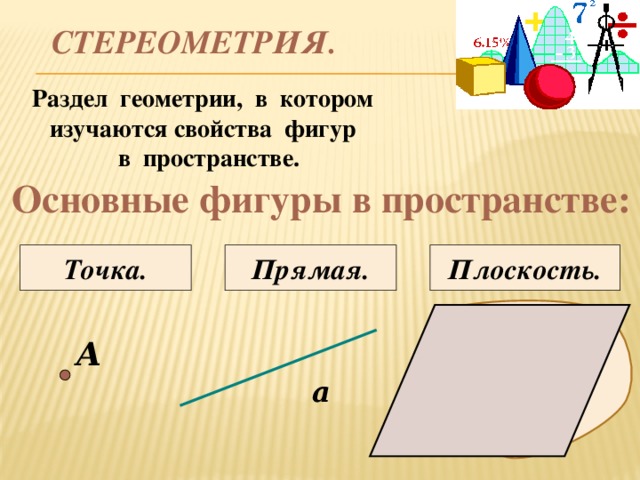
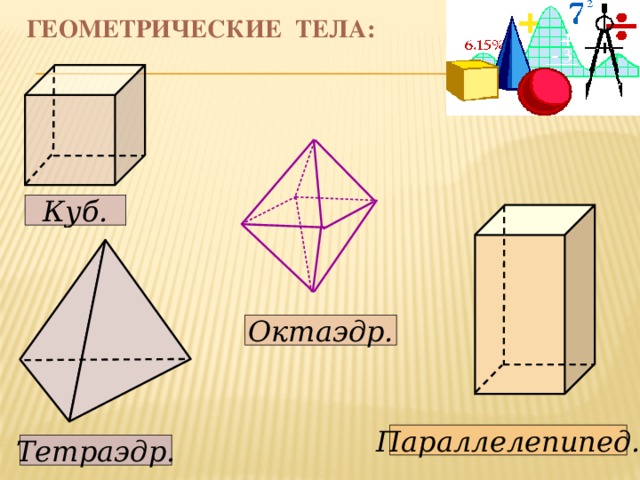
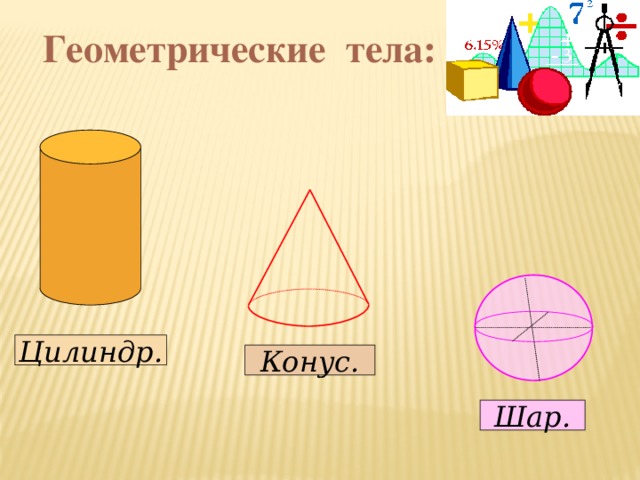
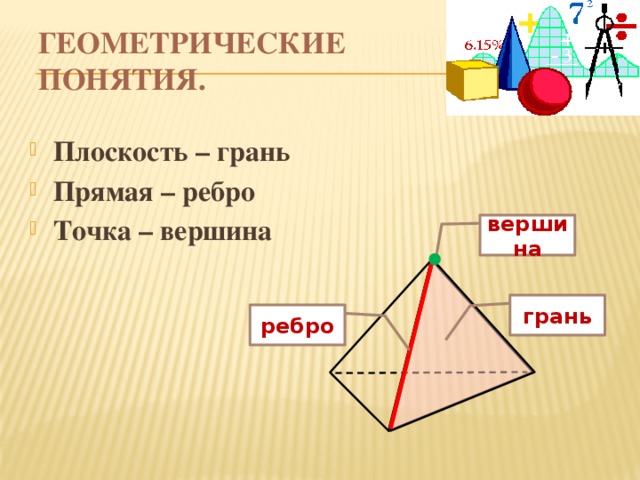
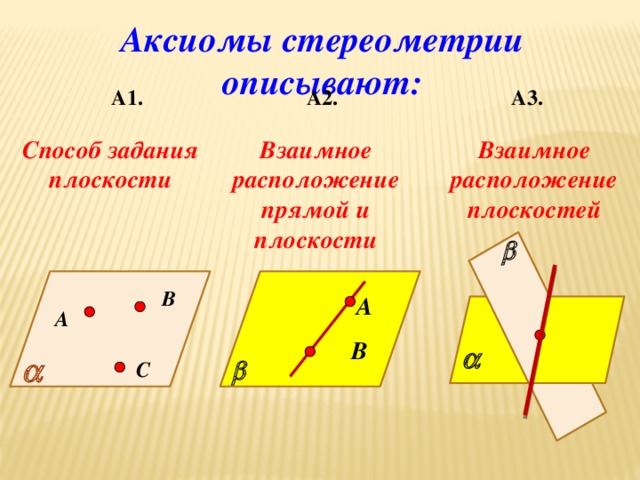
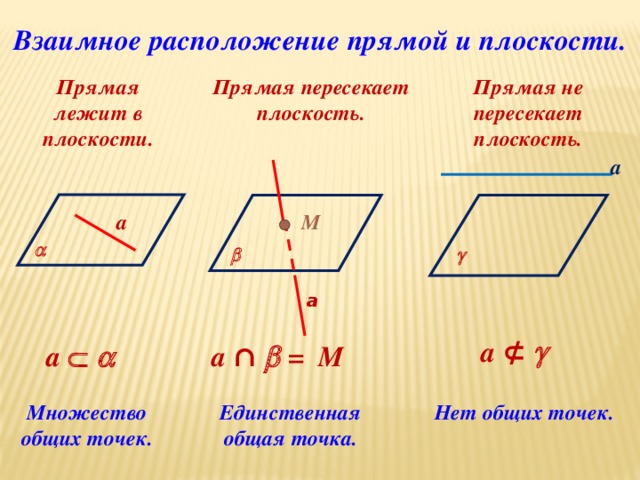
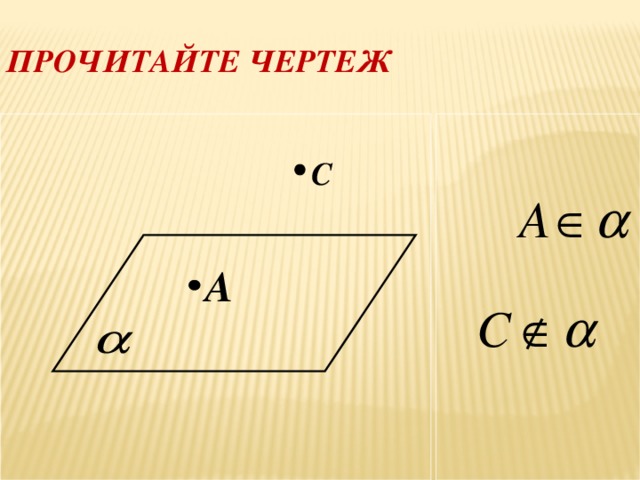
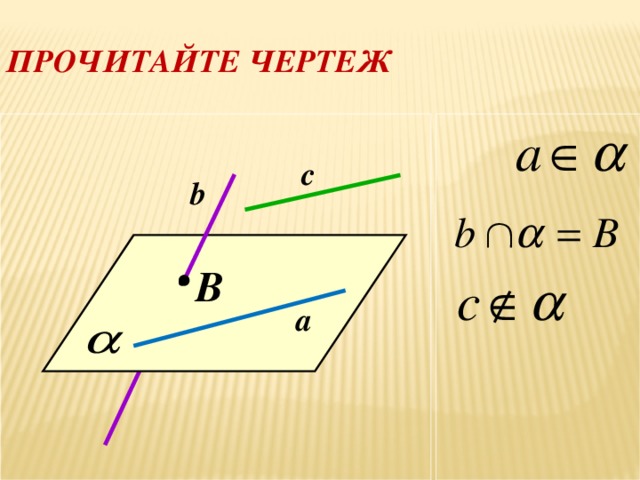
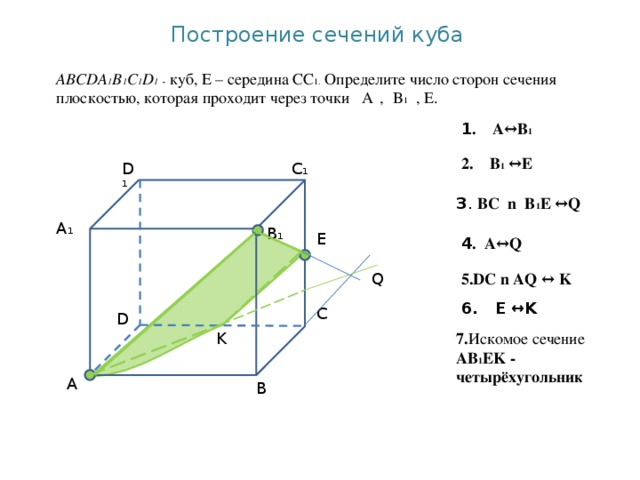
Построение сечений многогранников

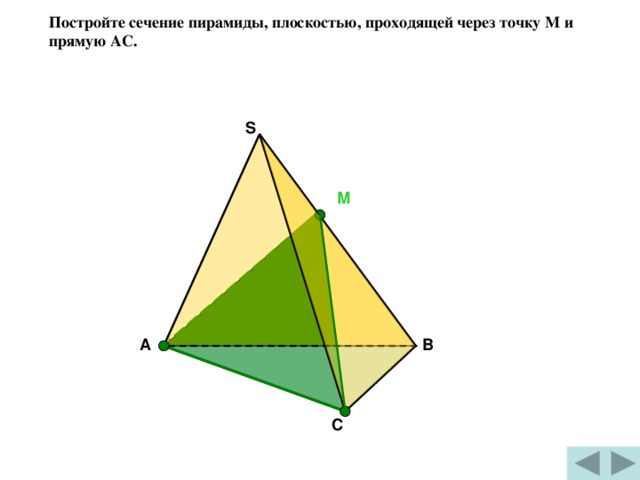
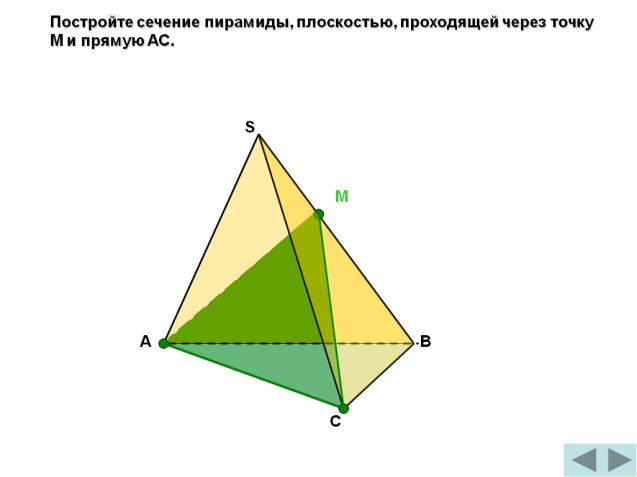
Постройте сечение пирамиды, плоскостью, проходящей через точку М и прямую АС.

S

М

• А↔М, т.к.А є( ABS) и М є (ABS)
• С↔М, т.к.Сє( СBS) и М є (СBS)
• АМС- искомое сечение. ( по т.15.1)

А

В

С

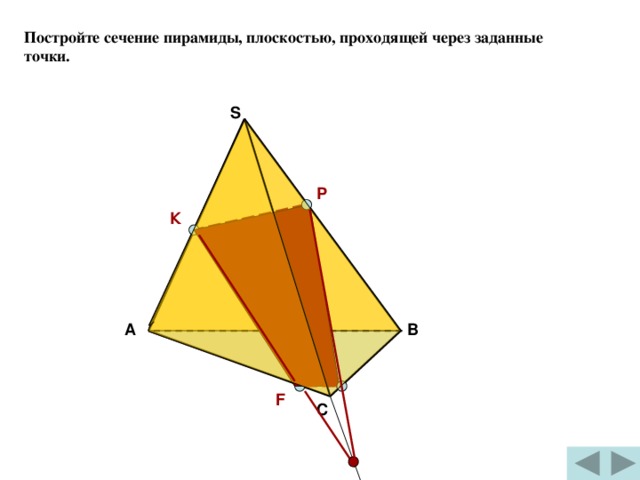
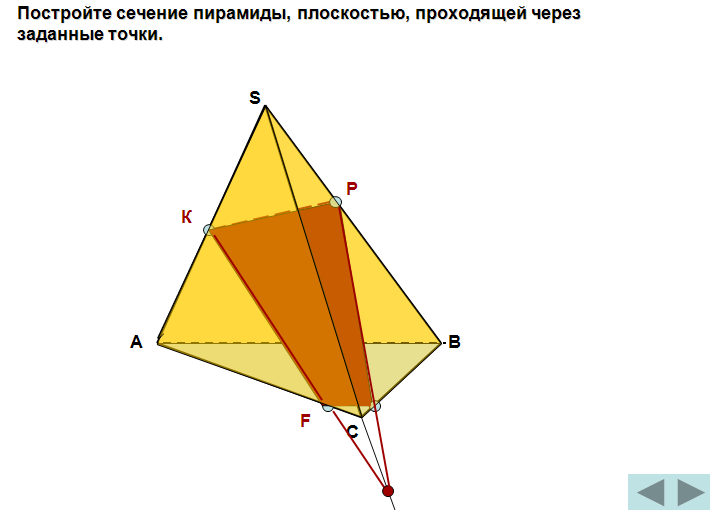
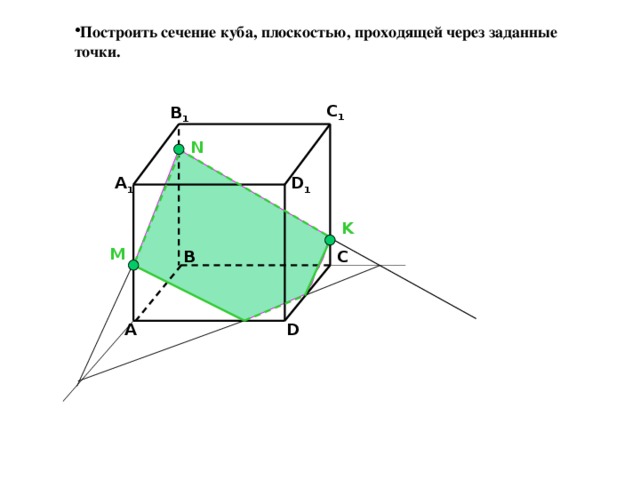
Постройте сечение пирамиды, плоскостью, проходящей через заданные точки.

S

Р

К

А

В

F

С

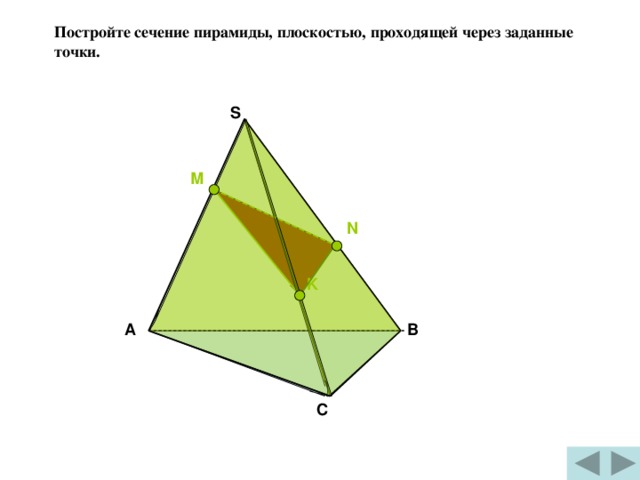
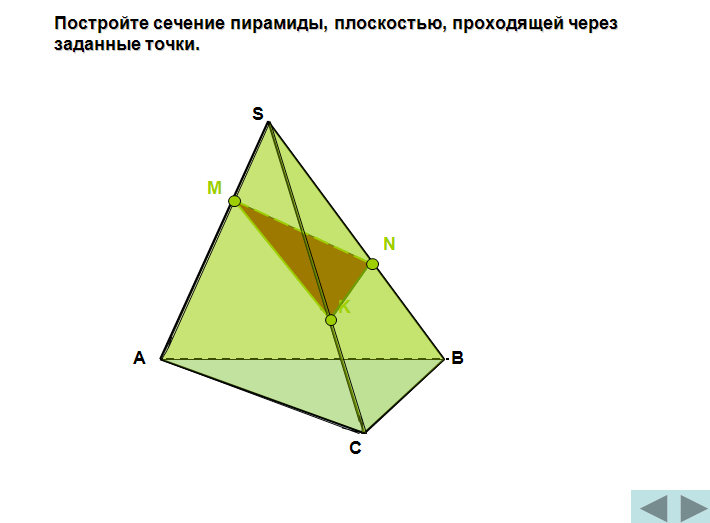
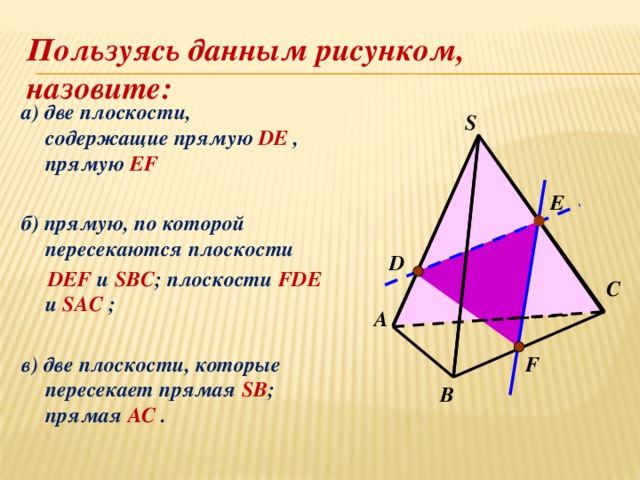
Постройте сечение пирамиды, плоскостью, проходящей через заданные точки.

S

М

N

K

А

В

С

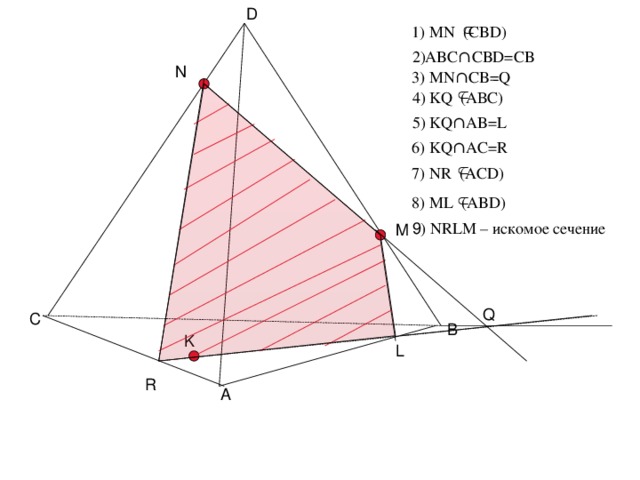
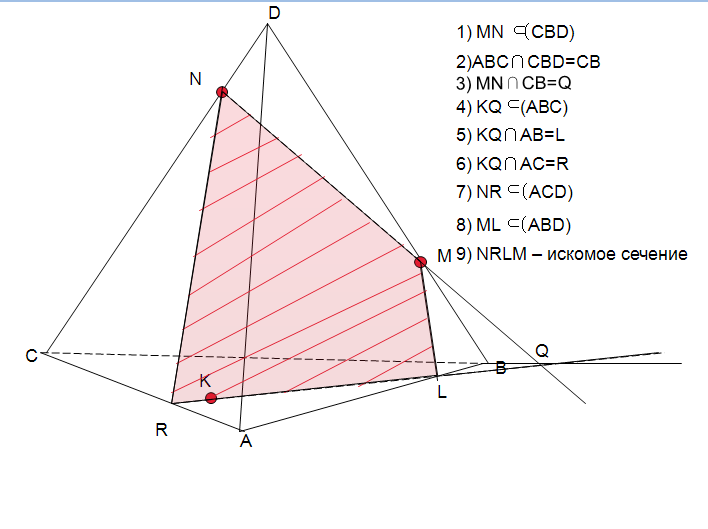
D

3) MN ∩CB=Q

5) KQ ∩AB=L

4) KQ (АВС)

1) МN (CBD)

2)ABC ∩CBD=CB

N

6) KQ ∩AC=R

7) NR (ACD)

8) ML (ABD)

9 ) NRLM – искомое сечение

M

Q

C

B

K

L

R

A

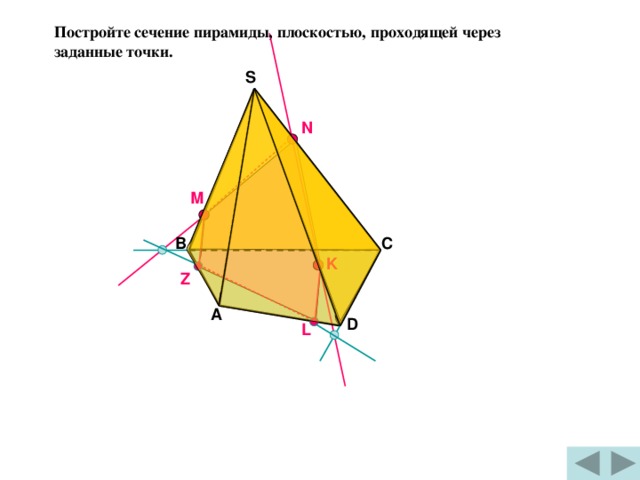
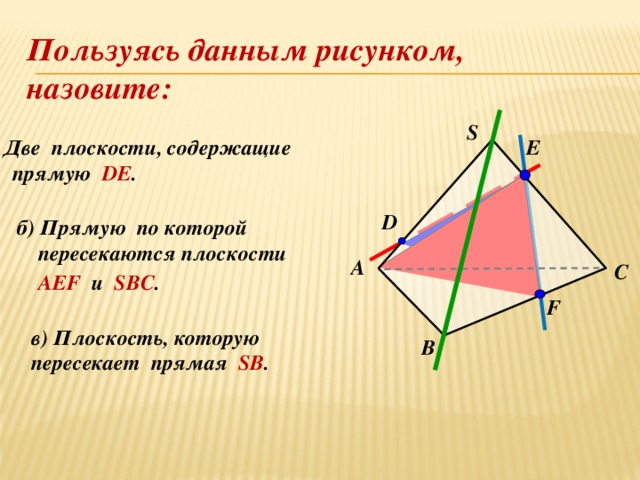
Постройте сечение пирамиды, плоскостью, проходящей через заданные точки.

S

N

М

B

C

K

Z

A

D

L

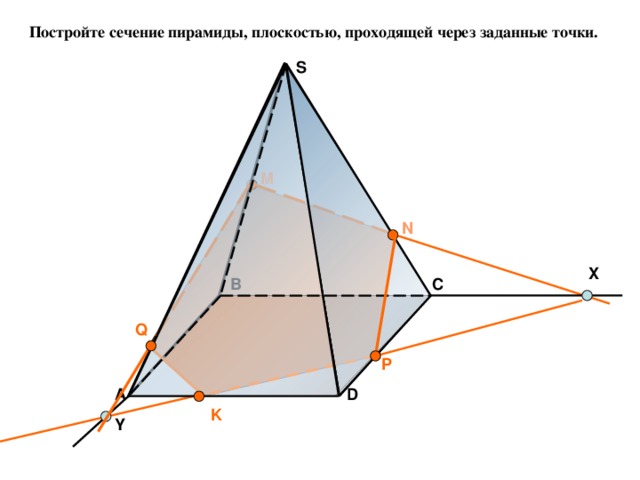
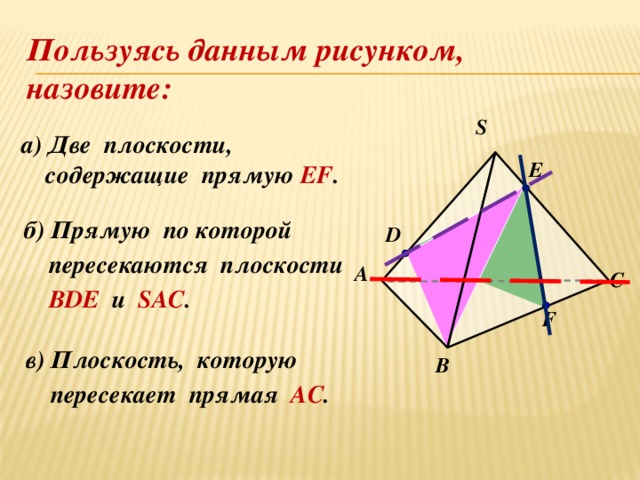
Постройте сечение пирамиды, плоскостью, проходящей через заданные точки.

S

M

N

X

C

B

Q

P

D

А

K

Y

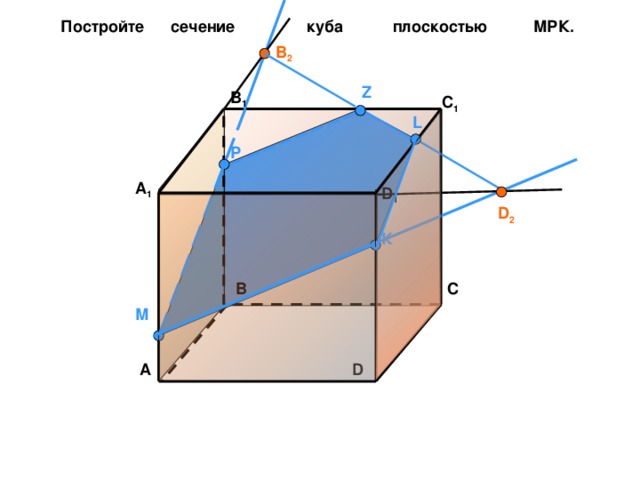
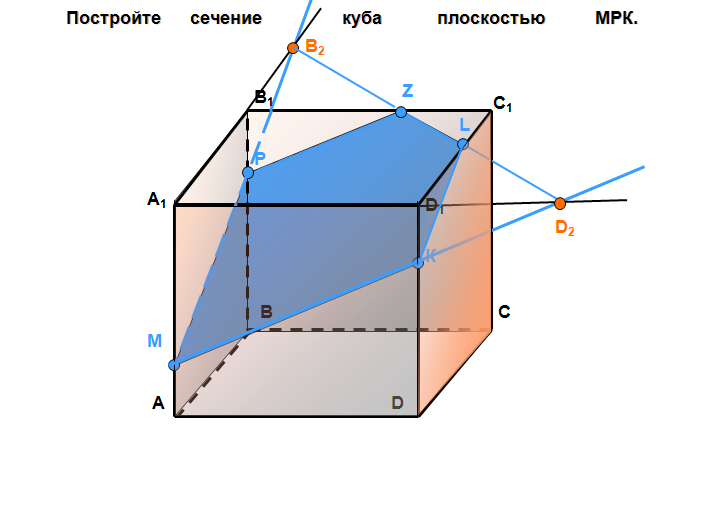
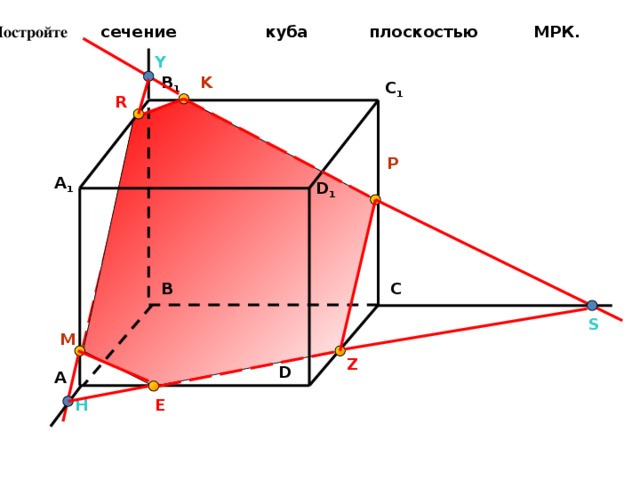
Постройте сечение куба плоскостью МРК.

B 2

Z

B 1

C 1

L

Р

A 1

D 1

D 2

К

В

С

М

D

А

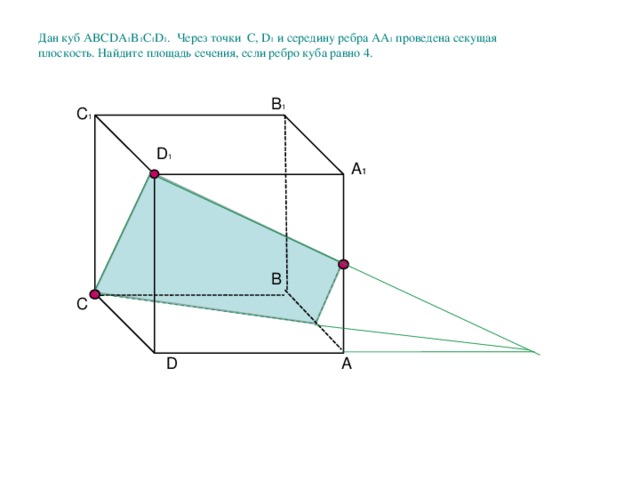
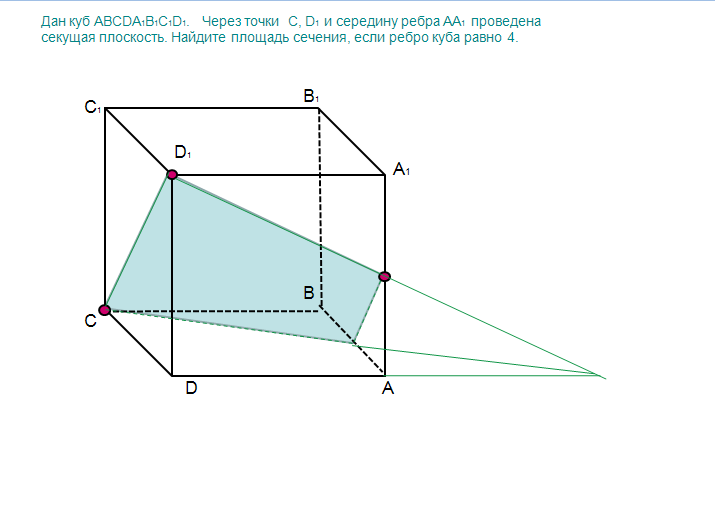
Дан куб ABCDA 1 B 1 C 1 D 1 . Через точки С, D 1 и середину ребра АА 1 проведена секущая плоскость. Найдите площадь сечения, если ребро куба равно 4.

B 1

C 1

D 1

А 1

В

С

D

А

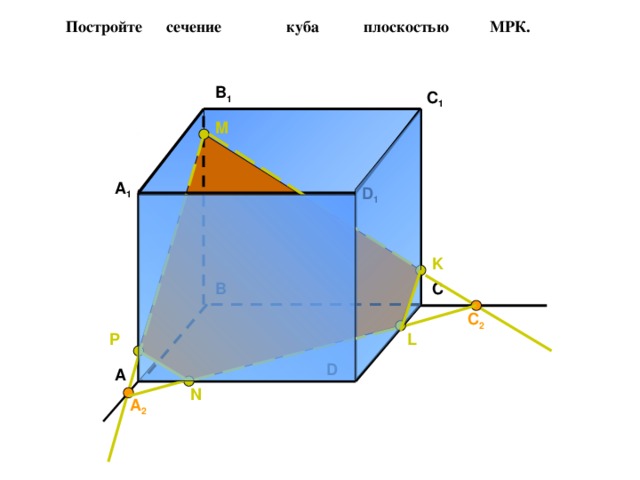
Постройте сечение куба плоскостью МРК.

B 1

C 1

M

A 1

D 1

K

C

B

C 2

L

P

D

A

N

A 2

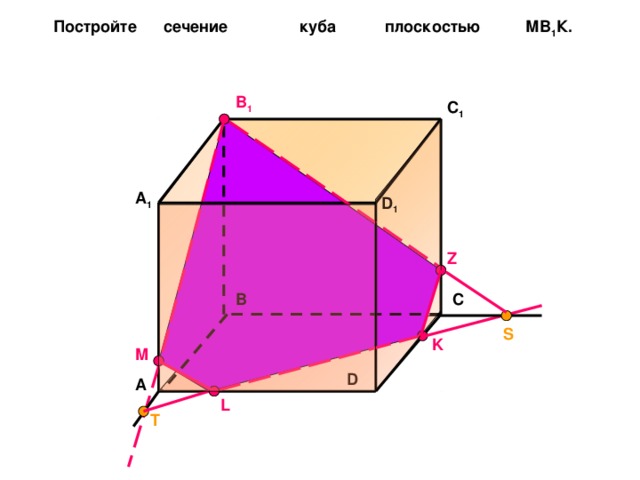
Постройте сечение куба плоскостью МB 1 К.

B 1

C 1

A 1

D 1

Z

B

C

S

K

M

D

A

L

T

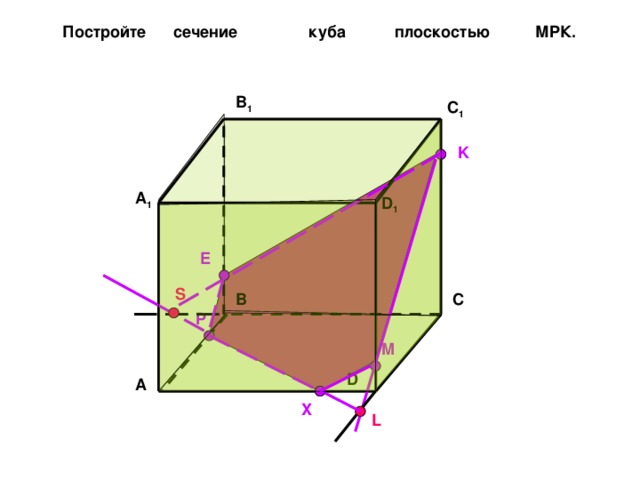
Постройте сечение куба плоскостью МPК.

B 1

C 1

K

A 1

D 1

E

S

B

C

P

M

D

A

X

L

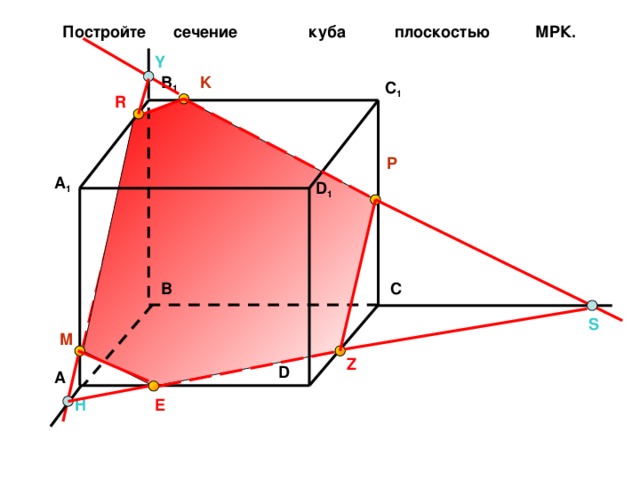
Постройте сечение куба плоскостью МPК.

Y

K

B 1

C 1

R

P

A 1

D 1

C

B

S

M

Z

D

A

E

H

13

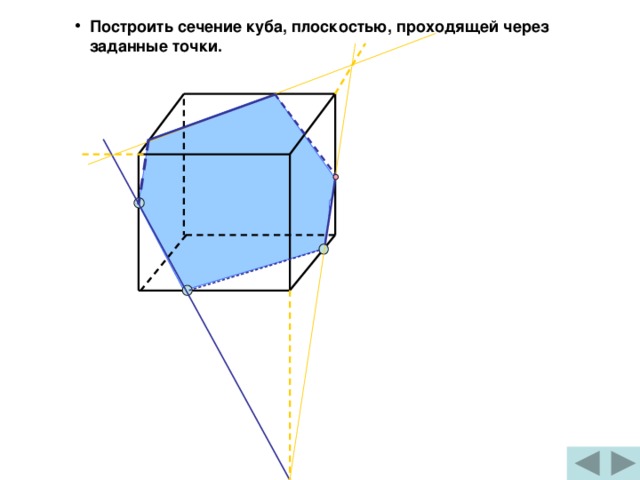
• Построить сечение куба, плоскостью, проходящей через заданные точки.

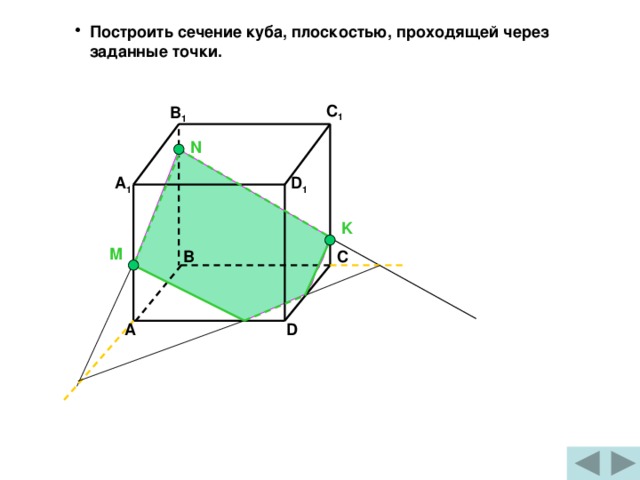
• Построить сечение куба, плоскостью, проходящей через заданные точки.

C 1

B 1

N

A 1

D 1

K

M

B

C

D

A

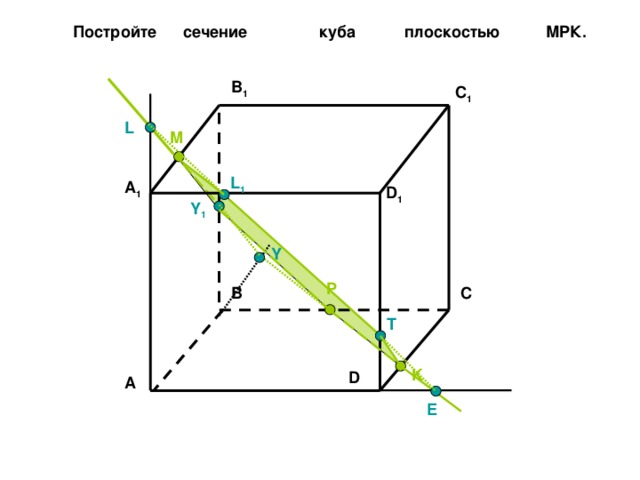
Постройте сечение куба плоскостью МPК.

B 1

C 1

L

M

L 1

A 1

D 1

Y 1

Y

P

C

B

T

K

D

A

E

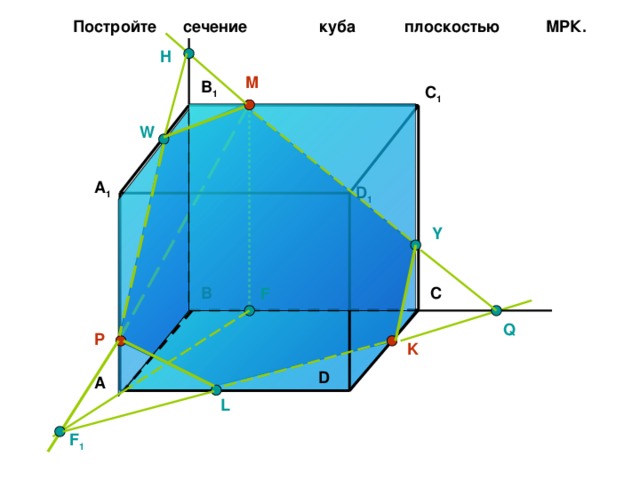
Постройте сечение куба плоскостью МPК.

H

M

B 1

C 1

W

A 1

D 1

Y

B

C

F

Q

P

K

D

A

L

F 1

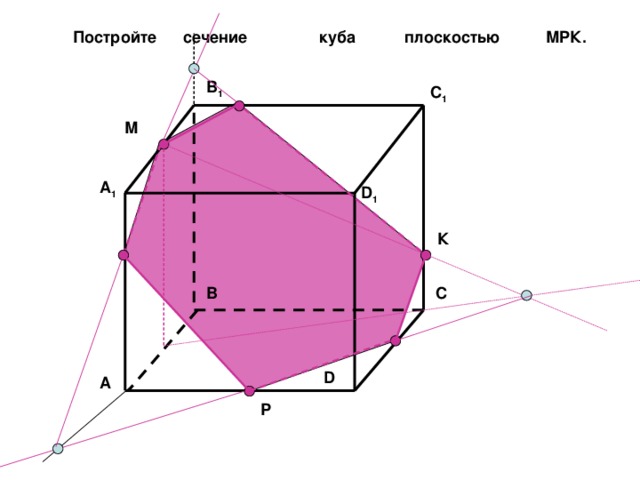
Постройте сечение куба плоскостью МPК.

B 1

C 1

М

A 1

D 1

К

C

B

D

A

Р

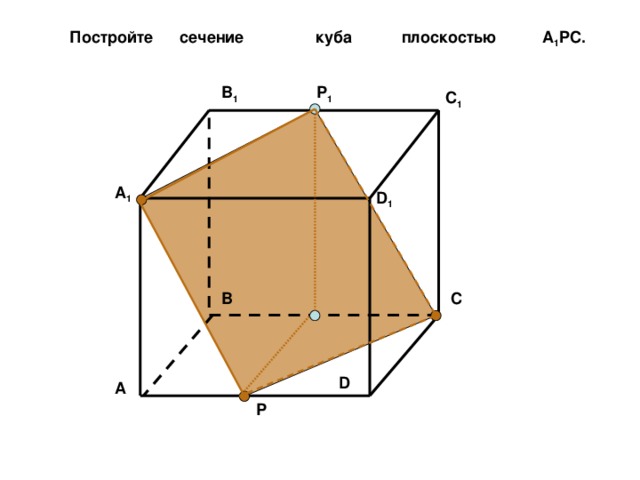
Постройте сечение куба плоскостью А 1 PС.

Р 1

B 1

C 1

A 1

D 1

C

B

D

A

Р

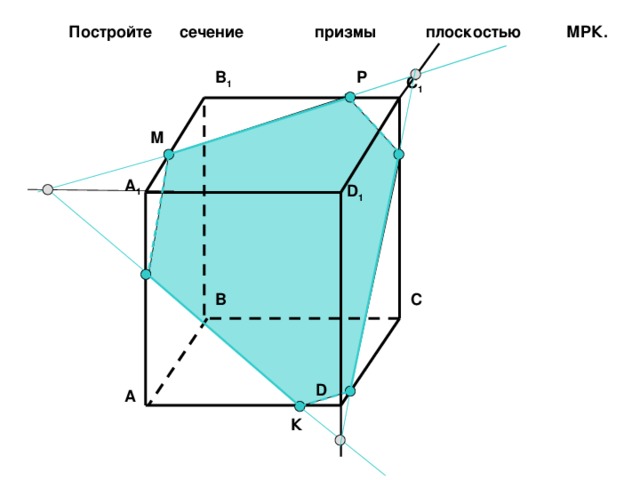
Постройте сечение призмы плоскостью МPК.

Р

B 1

C 1

М

A 1

D 1

C

B

D

A

К

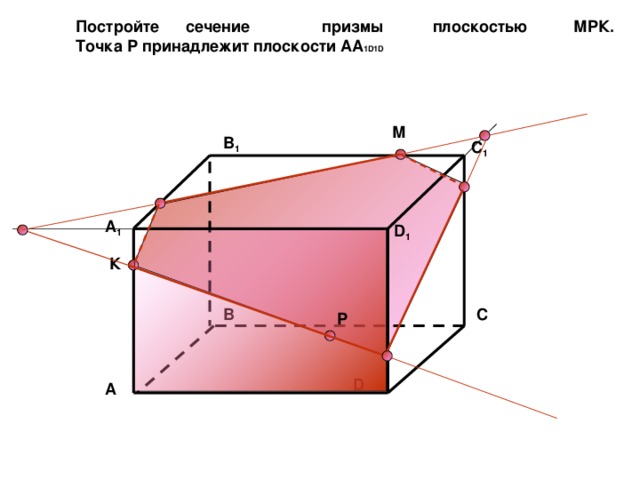
Постройте сечение призмы плоскостью МPК.

Точка Р принадлежит плоскости АА 1D1D

М

B 1

C 1

A 1

D 1

К

C

B

Р

D

A

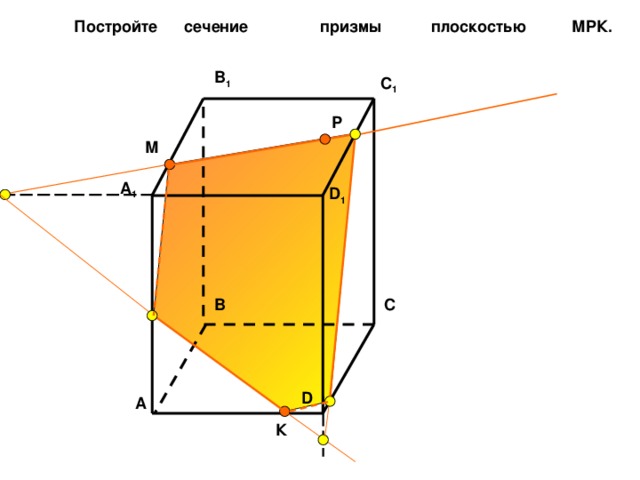
Постройте сечение призмы плоскостью МPК.

B 1

C 1

Р

М

A 1

D 1

C

B

D

A

К

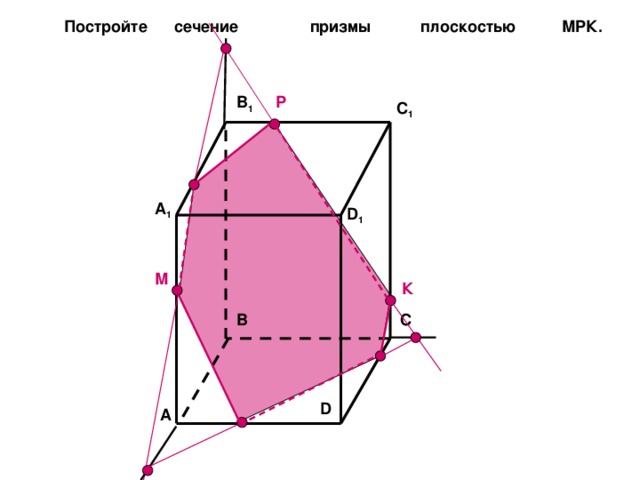
Постройте сечение призмы плоскостью МPК.

Р

B 1

C 1

A 1

D 1

М

К

C

B

D

A

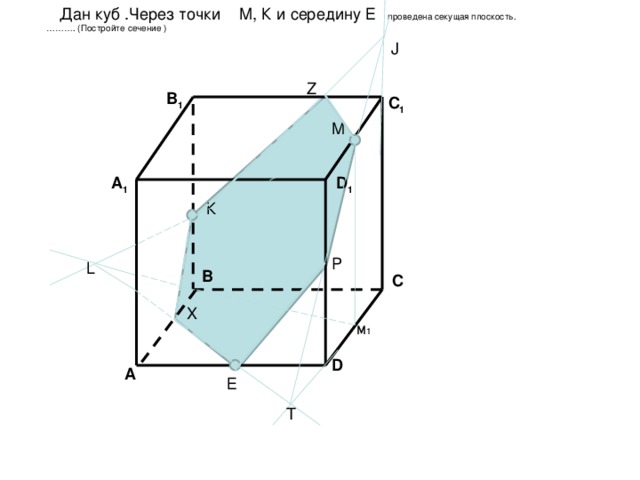
Дан куб .Через точки М, К и середину Е проведена секущая плоскость. ………. (Постройте сечение )

J

Z

B 1

C 1

М

A 1

D 1

К

P

L

B

C

X

м 1

1.Построим ортогональные проекции точек К и М на плоскость АВСD : это точки В и М 1 соответственно.

2. К↔М

3. КМ n BM1=L є ( АВСD)

4.L ↔E

5. K↔X

6. XE n CD = T ( XE и CD лежат в плоскости ABCD)

7. Т ↔ М ( принадлежат одной плоскости CC1DD1)

8. MT n DD1 = P

9.P↔E (принадлежат одной плоскости)

10.РМ n CC1= J

11. K↔J

12.KJ n BC1=Z

13. Z↔M ( принадлежат одной плоскости)

14. Искомое сечение KXEPMZ

D

A

Е

Т

24

Для преподавателя

• С 10 слайда упрощается объяснение, так как подразумевается, что ученики видят плоскость в которой находятся точки.
• Для дидактического материала быстро можно распечатать заготовки слайда.

Домашняя работа

• на « 3 » - построить сечение на бумажном носителе без описания;
• на « 4 » - построить сечение с пошаговым описанием построения;
• на « 5 » – построить сечение с полным обоснованием (пошаговым описанием построения и ссылками на аксиомы и теоремы).

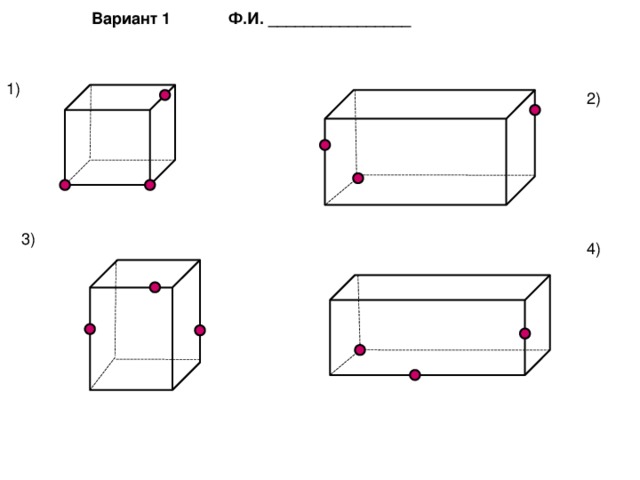
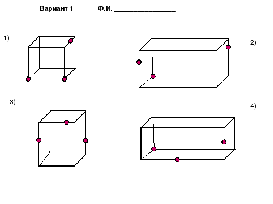
Вариант 1 Ф.И. ________________

1)

2)

3)

4)

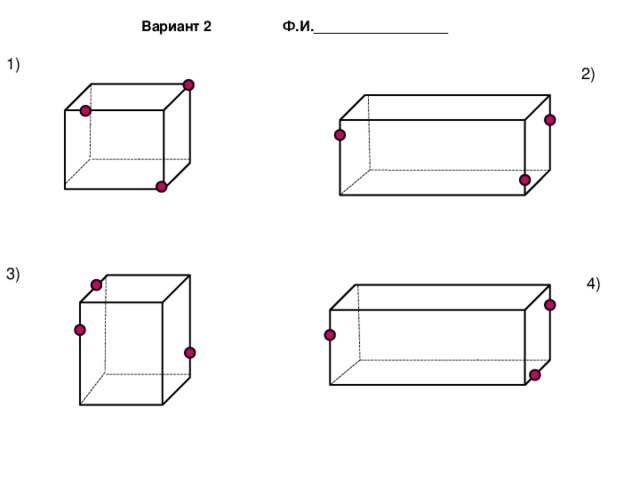
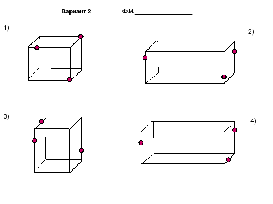
Вариант 2 Ф.И._________________

1)

2)

3)

4)

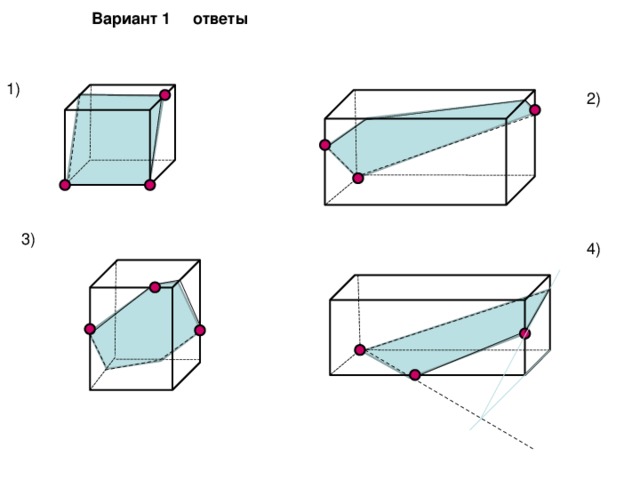
Вариант 1 ответы

1)

2)

3)

4)

1)Проверка домашней работы осуществляется с помощью данного слайда в течение 3-5 мин.

2)Пошаговое построение проговаривается устно.

24

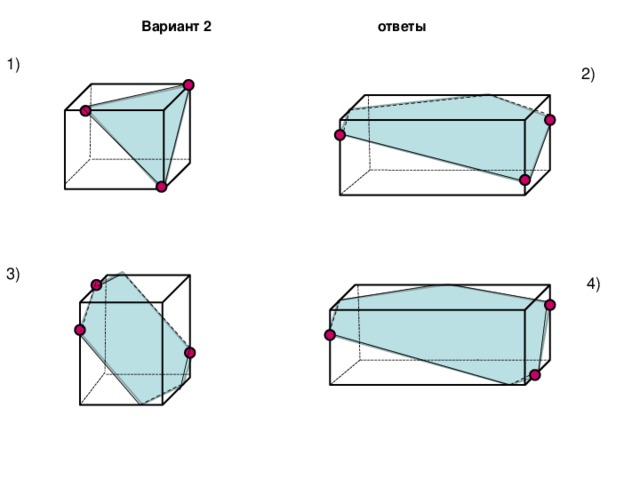
Вариант 2 ответы

1)

2)

3)

4)

Зачетная работа ( вариант)

В-1 В-2

1. сл.№5 1. сл.№6

2. сл.№ 10 2.сл.№11

3. сл.№16 3. сл.№17

2. Теоретический вопрос.

Существование плоскости

С1. Какова бы ни была плоскость , существуют точки, принадлежащие этой плоскости, и точки , не принадлежащие ей.

Т.15.1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

С2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Т.15.3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

С3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Для самостоятельного изучения

Существование плоскости

С1. Какова бы ни была плоскость , существуют точки, принадлежащие этой плоскости, и точки , не принадлежащие ей.

Т.15.1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

С2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Аксиомы и теоремы из учебника А.В.Погорелов 7-11

Т.15.3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

С3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Основной закон!

• Через две точки плоскости можно провести прямую и только одну.

Построение сечения пирамиды

задача: построить сечение ,проходящее через вершину D и точки М и N, лежащие на ребрах AB и BC тетраэдра ABCD

1.M↔N

D

2.M↔D

3.D↔N

4.Искомое сечение - ∆ MDN.

C

A

N

M

B

ПОЛНОЕ ОПИСАНИЕ ПОСТРОЕНИЯ К СЛАЙДУ №3

• 1.Через три точки всегда можно провести плоскость ( теорема 15.3.)
• ( обозначим её α) и притом только одну.
• 2.Так как точки М и Nявляются общими для плоскостей α и пл. АВС , то прямая MN является прямой пересечения этих плоскостей ( соединим точки M и N отрезком) ( по С2).
• 3. Подобными рассуждениями обосновывается возможность соединить точки М и D, и точки N иD .
• 4.Искомое сечение - ∆ MDN.

Построение сечения тетраэдра

Построить сечение тетраэдра ABCD плоскостью ,проходящей через точки M,N,P, лежащие , соответственно, на ребрах AD,DC и CB тетраэдра. Причем M и N заданы так, что прямые MN и AC не параллельны.

D

1.M↔N

2.N↔P

М

3.MN n AC ↔ Q

4. PQ n AB ↔ S

N

5. S ↔M

6.четырёхугол. SMNP – искомое сечение

Q

C

A

Р

S

В

Построение сечений куба

ABCDA 1 B 1 C 1 D 1 - куб, Е – середина СС 1. Определите число сторон сечения плоскостью, которая проходит через точки A , B 1 , E.

1 . A↔B 1

2. B 1 ↔E

C 1

D 1

3 . BC n B 1 E ↔Q

A 1

B 1

E

4 . A↔Q

Q

5.DC n AQ ↔ K

6. E ↔K

C

D

K

7. Искомое сечение AB 1 EK - четырёхугольник

A

B

• Построить сечение куба, плоскостью, проходящей через заданные точки.

C 1

B 1

N

A 1

D 1

K

M

B

C

A

D

Постройте сечение куба плоскостью МPК.

Y

K

B 1

C 1

R

P

A 1

D 1

C

B

S

M

Z

D

A

E

H

9