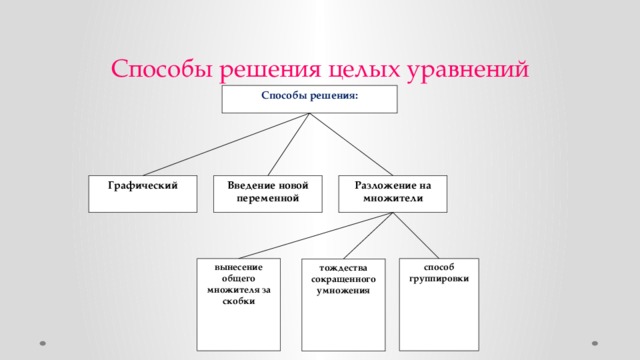
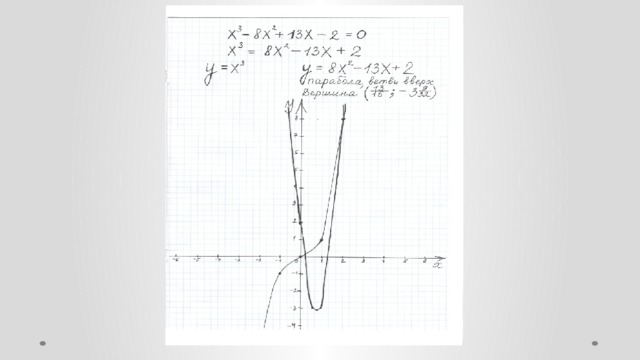
Предмет: алгебра. Класс: 9. Тема: Целые уравнения и способы их решения. Тип урока: обобщение и углубление (расширение) знаний. Оборудование: компьютер, мультимедийный проектор, экран. Приложение: презентация к уроку в программе PowerPoint (слайды). Цели урока: образовательные: систематизация и обобщение, расширение и углубление знаний учащихся по решению целых уравнений с одной переменной высших степеней; подготовка учащихся к применению знаний в нестандартной ситуации. развивающие: развитие личности обучающегося через самостоятельную творческую работу, развитие инициативы обучающихся; обеспечивать устойчивую мотивационную среду, интерес к изучаемой теме; развивать умение обобщать, правильно отбирать способы решения уравнения; воспитательные: развитие интереса к изучению математики, подготовка обучающихся к применению знаний в нестандартной ситуации; воспитывать волю и настойчивость для достижения конечных результатов.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Презентация к уроку по теме "Целые уравнения высших степеней и способы их решения".
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация к уроку по теме "Целые уравнения высших степеней и способы их решения". »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1230 руб.
1760 руб.
1970 руб.
2820 руб.
2100 руб.
3000 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства