| 1.Организационный момент. Учитель приветствует учащихся, проверяет их готовность к уроку.
Ребята! Девиз нашего урока: «Чем больше я знаю, тем больше я умею». А эпиграфом к уроку я взяла следующие слова: «Кто ничего не замечает, тот ничего не изучает. Кто ничего не изучает, тот вечно хнычет и скучает!» (поэт Р.Сеф.). Я думаю, что у нас сегодня на уроке скучно не будет!
2.Устная работа. На слайде записаны уравнения: 2х+5=10х-4 Х2-5х+6=0 Х3-6х=0 3х3-х2+18х-6=0 Х4-7х+12=0 Х4+х3-5х2+6х-2=0 Ребята, посмотрите на слайд. 1) Что вы видите? 2)А что такое уравнение? 3)Какие уравнения вы видите? 4)Что называется корнем уравнения? 5)Что значит решить уравнения?
6)Как называется первое уравнение? Каким способом оно решается? 7)Что вы можете сказать про второе уравнение? 8)Какова степень следующих уравнений?
Ребята! Уравнения, степень которых больше двух, мы будем называть уравнениями высших степеней.
Встречались ли вам такие уравнения? Если встречались, то какими способами вы их решали?
Как вы думаете, каким уравнениям мы сегодня посвятим наш урок? Попробуйте сформулировать тему нашего урока?
3.Актуализация и систематизация знаний.
Посмотрите на уравнения, представленные на слайде. х4 -2х2-8=0 х3-4х2-9х+36=0
х3-3х-2=0 х3-8х2+13х-2=0
Назовите степень каждого уравнения и способ его решения. Решите эти уравнения. Ребята, при решении четвёртого уравнения графическим способом, мы получим приближённые корни. Хорошо ли это? Какая перед нами стоит проблема? Можно ли найти точные корни известными вам способами?
Как же нам быть?
4.Целеполагание и мотивация.
Итак, ребята, что тогда будет целью нашего урока? Можете ли вы сформулировать цели урока?
5.Объяснение нового материала.
Ребята! Это уравнение можно решить применяя теоремы о корне многочлена и о целых корнях уравнения. Сейчас я вас познакомлю с ними.
Теорема 1.(О целых корнях уравнения). Если уравнение a0 xn + a1 xn-1 + … +an-1 x + an = 0 имеет целые коэффициенты, причём свободный член отличен от нуля, то целыми корнями такого уравнения могут быть только делители свободного члена.
Теорема 2.(теорема Безу). (О корне многочлена). Если число а является корнем многочлена Р(х)= a0 xn + a1 xn-1 + … +an-1 x + an = 0, то этот многочлен можно без остатка разделить на двучлен (х-а) и представить его в виде произведения (х-а)Р1(х), где Р1(х)-многочлен n-1ой степени.
Эта теорема позволяет решение целого уравнения n-ой степени для которого известен один из корней, свести к решению уравнения n-1ой степени.
Давайте теперь попробуем решить наше уравнение, используя данные теоремы. А для этого попытаемся составить алгоритм решения.
Ребята! Понятен ли вам этот способ? Будите ли вы его применять?
6.Физкультминутка!
Давайте немного отдохнём и сделаем небольшую зарядку.
7.Углубление и расширение знаний.
Продолжаем работу. Вы видите на слайде уравнение: х4-5х3+6х2-5х+1=0. Каким способом вы предложите его решить? Найдите целые корни этого уравнения. (Их нет.) Сделайте вывод. Как нам быть?
Посмотрите очень внимательно на это уравнение? Что вы заметили?
Ребята, уравнение такого вида, когда коэффициенты, равноудалённые от концов совпадают, называются возвратными. Это уравнение сводиться к квадратному с помощью подстановки. Предлагаю вам следующий алгоритм их решения :
Алгоритм решения возвратных уравнений.
1.Разделить обе части уравнения на х2 . 2.Сгруппировать слагаемые (первый с последним, второй с четвёртым). Привести уравнение к виду а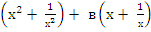 + с = 0 + с = 0
3. Ввести новую переменную t = 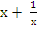 , тогда выполнено t2 = , тогда выполнено t2 = 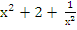 , т.е. , т.е. 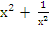 = t2 – 2. = t2 – 2.
4. Выполнить подстановку и решить квадратное уравнение. 5.Вернуться к замене и решить получившиеся уравнения. 6.Записать ответ.
Ребята, и ещё одно уравнение я хочу вам сегодня предложить, я его взяла из сборника задач для подготовки к ГИА. (х+1)(х+2)(х+4)(х+5) = 40 Если бы вы встретили такое уравнение, то как бы вы начали его решать?
Уравнения вида (х + а)(х + b)(x + c)(x + d) = А, где а + d = c + b называются симметрическими. Методика решения подобных уравнений заключается в частичном раскрытии скобок, а затем введении новой переменной. Показать решение этого примера на слайде.
8.Закрепление полученных знаний.
Я вам предлагаю по аналогии самостоятельно решить следующее уравнение (х-1)(х-3)(х+5)(х+7) = 297
Проверим ваше решение.
9.Подведение итогов урока. Рефлексия.
И так ребята, наш урок подошёл к концу. Давайте подведём итоги нашего урока.
Какие цели мы ставили в начале урока? Наши цели достигнуты? Что нового мы узнали на уроке? Как вы можете оценить свою работу?
Сегодня вы хорошо поработали, особенно активны были….. Кто работал у доски, получают оценки.
Запишите домашнее задание.
А закончить урок мне хочется словами великого учёного Эйнштейна А. : « Мне приходиться делить своё время между политикой и уравнениями. Однако уравнение, по – моему, гораздо важнее, потому что политика существует только для данного момента, а уравнение будет существовать вечно».
Спасибо за урок! До свидания !
|
Учащиеся готовы к началу работы.
Ребята смотрят на слайд и отвечают на вопросы учителя. 1) Это уравнения. 2).Уравнение – это равенство, содержащее переменную. 3).Это целые уравнения, в которых левая и правая части являются целыми выражениями. 4).Это значение переменной, при котором уравнение обращается в верное числовое равенство. 5).Это значит найти все его корни или доказать, что корней нет. 6)Это уравнение первой степени (линейное). 7)Уравнение второй степени, квадратное. Решаем по формулам или теореме Виета. 8)Третья и четвёртая степени!
Да! Встречались, но очень редко. Называют известные способы решения целых уравнений: разложение на множители (вынесение за скобки, группировка, формулы сокращённого умножения); подстановка (введение новой переменной); графический способ.
Уравнениям высших степеней. Называют тему урока: «Целые уравнения высших степеней и способы их решения». Записывают тему в тетрадях.
Ученики называют способ решения уравнения, решают уравнения на доске. 1.Биквадратное (введение новой переменной). 2. Разложение на множители (группировка).
3.Графический способ. 4.Пытаються решить графическим способом, но получают не точные корни, а приближённые. Это не очень хорошо. Определяют проблему – как найти точные корни уравнения? Можно ли это сделать? Нам не хватает знание известных способов.
Нам нужно узнать новые способы, которые помогут решить уравнения такого вида.
Формулируют цели урока - узнать новые способы решения целых уравнений высших степеней и научиться применять их при решении уравнений.
.
Слушают объяснение учителя.
Составляют алгоритм решения уравнения, записывают его в тетради.
Алгоритм: 1. Найти делители свободного члена. 2.Среди делителей найти корень уравнения путем проверки. 3.Разделить многочлен правой части уравнения на выражение ( х-а), где а – найденный путем подбора корень уравнения (деление уголком). 4.Разложить многочлен на множители. 5. Найти корни уравнения. 6.Записать ответ.
По алгоритму решают уравнение. Делают вывод о нахождении точных корней.
Делают вывод о необходимости знания этого способа.
Учащиеся повторяют упражнения за учителем!
Ребята предлагают решить его с помощью изученных теорем. Устанавливают подбором, что целых корней нет. Делают вывод, что это уравнение нельзя решить с помощью теорем. Ищем иной способ.
Внимательно смотрят на уравнения и делают вывод, что в этом уравнении коэффициенты равноудалённые от концов равны.
Ребята изучают алгоритм. Ученик у доски по алгоритму и с помощью учителя решает уравнение, остальные пишут в тетрадях.
Предлагают свои способы решения.
Записывают определение в тетрадь. Разбирают решение примера.
Решают уравнение самостоятельно. Затем сверяют своё решение и готовое решение на слайде.
Подводят итоги урока, делают выводы.
Записывают домашнее задание.
|