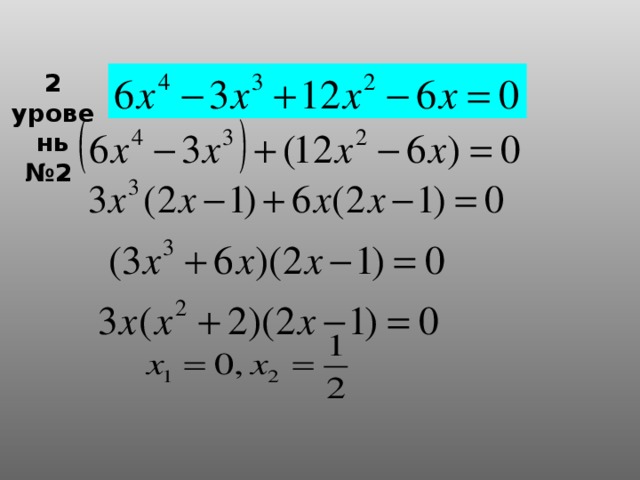Автор: Жданова Мария Власовна, учитель математики,
МАОУ «Кондратовская средняя общеобразовательная школа»
Методическая разработка открытого урока алгебры (9 класс)
в рамках комплексной проверки школы 28.11.2012г.
Тема: «Решение целых уравнений различными методами».
(УМК: Алгебра. 9 класс. Макарычев Ю.Н., Миндюк Н.Г. и др.)
Цель урока: обобщить и систематизировать знания о целых уравнениях и методах их решений.
Задачи урока
1. Образовательные: закрепить, систематизировать, обобщить знания, умения и навыки решения целых уравнений различными способами. Актуализировать опорные знания решения линейных, квадратных уравнений и уравнений высших степеней
2. Развивающие: развивать умения в применении знаний в конкретной ситуации; развивать логическое мышление, умение работать в проблемной ситуации; умение обобщать, конкретизировать, правильно излагать мысли; развивать самостоятельную деятельность учащихся.
3. Воспитательные: поддерживать интерес к предмету через содержание учебного материала; развивать умение работать в коллективе и в паре, взаимопомощь, культуру общения, умение применять преемственность в изучении отдельных тем; воспитывать настойчивость в достижении цели, умение не растеряться в проблемных ситуациях.
Оборудование: мультимедийный проектор, компьютер, экран, презентация учителя, карточки для учащихся, карточки с уравнениями, учебник, листы самоконтроля для учащихся, доска, мел.
Ход урока
ЭТАП 1. Вхождение в тему урока и создание условий для осознанного
восприятия материала.
(Вводно-мотивационная часть, с целью активизации деятельности учащихся)
1.1. Организационный момент (слайд 1).
- Доброе утро, ребята! Садитесь. (слайд 2).
- Ребята, перед вами красивое дерево, часть дерева скрыта от нашего взгляда. Что у дерева мы не видим? Без нее дерево не живет (корни).
- Да, верно ( на слайде у дерева появляются корни).
- На каких уроках вы встречались со словом «корень»? Что имеет корень? (Корень есть у слова, без корня слово рассыпается, корень зуба, корень языка, корни волос, в переносном смысле – мои корни (родословная), корень проблемы, корень зла… )
- В математике тоже есть корни. Какие? (Квадратные корни, корни многочленов, при решении уравнений мы находим корни, значения переменных, которые обращают уравнение в верное числовое равенство).
1.2. Устная работа.
(слайд 4; слайд 5).
- Найдите корни уравнений
(Ответы: (-2); (0,5); (-4; 4); (0;-3; 3); (нет корней); (0); (любое);(15); (-1); (2; 3);
(-5; 5; -10; 10); (0;-1;-44 4)).
(На доске уравнения с номерами)
- Ребята, какое из данных уравнений лишнее? Почему?
(Лишнее под № 2 т. к. дробно- рациональное, а остальные уравнения целые).
- Дайте определение целого уравнения с одной переменной.
(Если левая и правая части представляют собой целые выражения, то это уравнение называется целым)
-Распределите данные уравнения на 3 группы.
(Линейные, квадратные, уравнения высших степеней)
- Сколько корней может иметь линейное уравнение ах+в=0, квадратное уравнение, уравнение третьей степени,… уравнение п-ой степени.
(Уравнение п-ой степени имеет не более п корней)
-Какие методы решения целых уравнений с одной переменной вы знаете?
(Аналитический и графический)
- Какие аналитические методы можно применить для решения уравнений высших степеней?
(Метод разложения, метод введения новой переменной)
1.3. Целеполагание.
- Итак, сформулируйте тему нашего урока?
( Решение целых уравнений различными методами) (слайд5)
- Ребята, какие цели вы ставите на этом уроке? Пожалуйста, я вас прошу зафиксировать свои цели в оценочном листе.
- Итак, цель нашего урока: «обобщение и систематизация знаний о целых уравнениях с одной переменной и методах их решений (слайд 6).
- Откройте тетради, запишите число 28.11.12. и тему урока «Решение целых уравнений различными методами».
ЭТАП 2. Организация и самоорганизация учащихся в ходе дальнейшего
усвоения материала. Организация обратной связи.
- Вспомним алгоритмы решения целых уравнений с одной переменной. Работаем в тетрадях. (3 ученика решают уравнения у доски) (слайд 7)
- Вспомним алгоритм решения целых уравнений методом введения новой переменной. (Ученик решает у доски) (слайд 8).
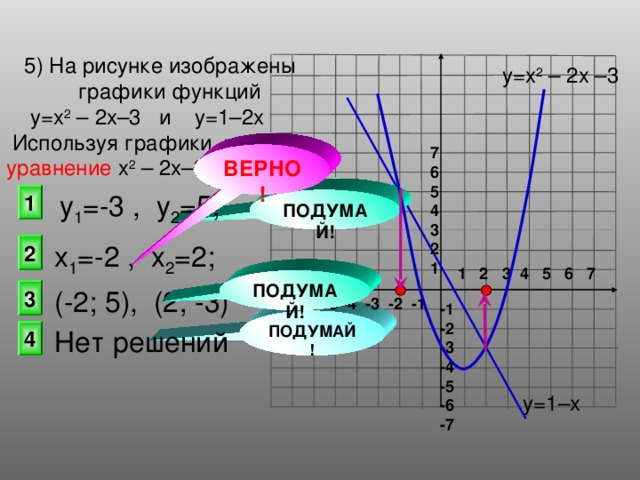
- Используя графики функций решите уравнение графически. (Фронтальная проверка и оценка) (слайд 9) (слайд 10)
- Вывод: графические способы красивы, но не дают гарантии решения любого уравнения.
Этап 3. Практикум.
Работа в парах (слайд 11).
- «Умение решать задачи–практическое искусство, подобное плаванию, или катанию на лыжах: научиться этому можно лишь подражая избранным образцам и постоянно тренируясь…»
- На парте есть задания на карточке, работаем в парах. Выберите уровень. (Проверка у доски по готовности, выходим парой).
(слайд 12-15)
(Проверка полученных результатов. Коррекция.)
ЭТАП 4. Тестирование. (слайд 16)
(Проверка полученных результатов. Коррекция.)
ЭТАП 5. Рефлексия.
- Вернемся к цели урока. Достигли ли вы на уроке поставленной цели?
- Какие затруднения возникли при работе на уроке? Почему? (слайд 17)
- Какие методы и приемы можно применить при решении уравнений высших степеней?
- При решении уравнений какой метод вызывает у вас затруднения?
- Оцените свою работу и поставьте себе отметку за урок в оценочном листе.
- Сегодня вы действительно хорошо поработали. Итоговая отметка за урок будет выставлена после анализа оценочных листов (слайд 18) .
- Запишем домашнее задание (слайд 19).
- «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться находить корни уравнений, то решайте их. Уравнения являются математическими моделями реальных ситуаций». (слайд 20)
- Урок окончен. Спасибо!
5