Занятие элективного курса предпрофильной подготовки в 9 классе.
Тема занятия: «Схема Горнера и её применения»
Цели: 1. В направлении личностного развития: развитие интереса к математическому творчеству и математических способностей
2. В метапредметном предметном направлении: формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности
3. В предметном направлении: овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни
Задачи:
Образовательные:
• научить находить значение многочлена, его корни, используя теорему Безу, схему Горнера;
• сформировать у учащихся умения и закрепить навыки решения алгебраических уравнений;
• научить применять ключевые задачи не только в знакомой, но и в модифицированной и незнакомой ситуациях.
Развивающие
• развить умения самостоятельного решения уравнений и задач, связанных с преобразованием многочленов;
• содействовать развитию устойчивого интереса к математике с помощью математической строгости умозаключения;
• ознакомить с логическими приемами мышления.
Воспитательные:
• воспитать чувство ответственности, формировать навыки самооценки;
• содействовать желанию расширить и углубить знания, полученные на уроке,
• воздействовать на мотивацию к учению с помощью историко-математического материала;
• содействовать повышению грамотности устной и письменной речи учащихся.
Тип урока: урок « открытия» новых знаний
Результаты обучения: 1. Личностные: Представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации
2. Метапредметные: Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
3. Предметные: Овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
Оборудование: компьютер, проектор, экран, маркерная доска, карточки с заданиями
Форма организации учебной деятельности: Индивидуальная, фронтальная, групповая, самопроверка.
План урока:
1. Организационный момент: вступительное слово учителя о цели занятия
2. Актуализация опорных знаний (10 мин.):
1) Повторение теории о многочленах: (вопросы учащимся)
a. Что мы называем многочленом? ( Что называется одночленом? Когда одночлен представлен в стандартном виде?)
Примеры: 2х2+3у; 7х5у3-5х2у+7х-5; 6х5+9х4-8х+6
b. Сколько переменных может входить в многочлен? С многочленами скольких переменных мы чаще всего работаем?
c. Когда многочлен представлен в стандартном виде?
Примеры: 6х4+х3-х; х7+х6-6х5+х2-5х; х3+5х2+11х+7;
2) Как определить степень многочлена, находящегося в стандартном виде?
Определите степени многочленов.
Разложение многочлена на множители:
a. Что значит разложить многочлен на множители?
b. Какие способы разложения мы знаем?
Учащиеся у доски выполняют разложения:
1.Вынесением за скобку общего множителя:
5х3+10х=5х(х2+2)
2.С помощью группировки:
х3+3х2-25х-75= (х2-25)(х+3)
3.С помощью формул сокращённого умножения:
25х2-36=(5х-6)(5х+6)
16х2-80х+25=(4х-5)2
3. Постановка проблемы.
Разложите многочлен на множители: 3х3+2х2-х-4=
Учитель: Эта задача не поддаётся известным способам, но выход есть. Нужно подбором найти хотя бы одно значение х, при котором значение многочлена равно нулю.
Учащиеся ищут значение х=1. Остальной ход смотрят на слайде 2.
3х3+2х2-х-4=(х-1)(3х2+5х+4)+0
Учитель: Наш многочлен разложился на два множителя. Всегда ли это возможно? Да, если х=а – корень многочлена.
4. Изучение нового материала
Учитель: Перепишем данное равенство в виде: (3х3+2х2-х-4) : (х-1)= (3х2+5х+4)
Говорят ещё, что многочлен 3х3+2х2-х-4 разделили на двучлен (х-1) нацело.
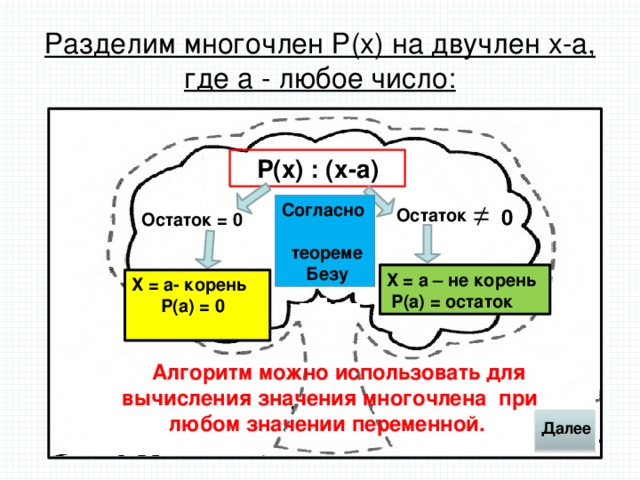
На это есть специальная теорема – теорема Безу( слайд 3)
Учащиеся записывают теорему в тетради.
Понравился ли вам такой способ разложения? Очевидно, нет, из-за его трудоёмкости. Но есть два других способа, более лёгких.
1 способ. Деление «уголком»
Разбор метода на слайде 4.
Попробуйте самостоятельно выполнить такое разложение, предварительно отыскав корень многочлена.
Кстати, его легко найти, зная тот факт, что он находится среди делителей свободного члена многочлена.
Задание1(выполняется на доске): 1. Разложить на множители многочлен:
х3-2х2-5х+6=(х-1)(х2-х-6)
2. Разложить на множители многочлен:
х3+5х2+11х+7=(х+1)(х2+4х+7)
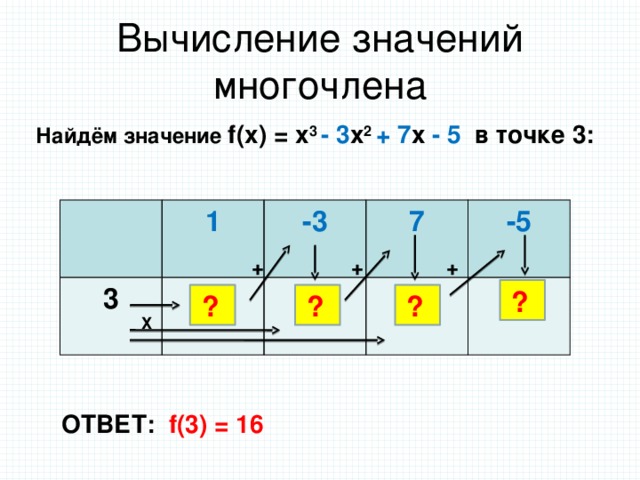
Учитель: Но и это не предел! Есть способ ещё более быстрый и лёгкий. Это применение схемы Горнера.(СЛАЙД 4).
Учащиеся разбирают схему Горнера, заносят в тетради алгоритм. Учитель рассказывает о Джордже Горнере(слайд 6)
С помощью схемы Горнера можно «автоматизировать» и процесс нахождения корней многочлена. Раньше вы искали их подбором, а теперь можно применить схему Горнера. Ведь если последнее число в таблице 0, то взятое число – корень многочлена. (Слайд8)
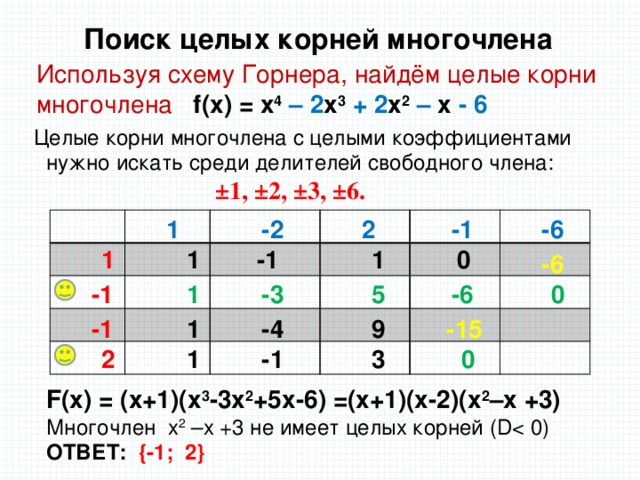
Задание2: Разложите многочлен на множители, используя схему Горнера:
х4+3х3-13х2-9х+30=(х-2)(х+5)(х2-3)
1 3 -13 -9 30
1 1 4 -9 -18 12
-1 1 2 -15 6 24
2 1(х3) 5(х2) -3(х) -15 0
-2 1 3 -9 3 -6
3 1 8 21 48 144
-3 1 2 -9 3 -9
5 1 10 47 220 1100
-5 1(х2) 0(х) -3 0 0
5. Актуализация новых знаний.
Учитель: Ребята, а зачем мы раскладываем многочлен на множители?
Учащиеся дают ответы: чтобы сокращать дроби и т.д.
Учитель: А если мы приравняем многочлен к нулю, то что получим? Верно, уравнение. Уравнение той же степени, что и многочлен.
Каких степеней уравнения мы умеем решать?( Первой, второй, биквадратные и некоторые третьей)
Как мы их решаем? (по формулам)
А если многочлен разложен на множители?(приравниваем к нулю каждый множитель).
Но теперь мы можем разложить любой многочлен на множители, а значит…можем решать уравнения высших степеней.
Учащиеся разбирают решение уравнения пятой степени(Слайд 9)
6. Практическое применение новых знаний
Задание 3.(на доске)
Решить уравнение, разложив на множители левую часть.
1)Х3+5х2+5х-3=0
Х=-3-корень, дальше по схеме Горнера
1 5 5 -3
-3 1 2 -1 0
Х3+5х2+5х-3=(х+3)(х2+2х-1)=0 ( Квадратное уравнение решаем по формуле.)
Ответ: { -3; -1-√2; -1+√2}
3) Решить уравнение х4-3х3-8х2+12х+16=0
1 -3 -8 12 16
1 1 -2 -10 2 18
-1 1 -4 -4 16 0
х4-3х3-8х2+12х+16=(х+1)(х3-4х2-4х+16)=0
1 -4 -4 16
-1 1 -5 1 15
1 1 -3 -7 9
2 1 -2 -8 0
х4-3х3-8х2+12х+16=(х+1)(х-2)(х2-2х-8)=0 ( Квадратное уравнение решаем по формуле.)
Ответ: {-1;2;4;-2}
7. Самостоятельная работа в группах
Учащиеся объединяются в группы по 4 человека. Группы с нечётными номерами решают вариант 1, а группы с чётными номерами – вариант 2.
Вариант 1.
Решить уравнение: х3-4х2+х+6=0
Вариант 2.
Решить уравнение: х3-3х2+6х-4=0
8. Рефлексия
Учащиеся ставят «+» возле смайликов: весёлого( всё понял), озабоченного( понял, но не всё), грустного(ничего не понял)
9.Подведение итогов.
Учитель: Какова же была цель нашего занятия? Что вы научились делать на занятии? С чего вы начнёте дома решение уравнений высших степеней? Объясните алгоритм действия Схемы Горнера.
10. Домашнее задание
1.Найти корни многочлена по схеме Горнера:
а) f (x) = x 3 + 2 x 2 – 5 x – 6;
б) f (x) = x 5 – 5 x 4 + 6 x 3 – x 2 + 5 x – 6;
2. Решить уравнения
а) х3 - 7 х + 6 = 0
б) 6 х3 + 11х2 +3 х – 2 = 0
Список используемых ресурсов
1. Методика преподавания темы «Схема Горнера, теорема Безу и деление уголком».
Из копилки приемов репетитора по математике Колпакова А.Н., 2010г.
http://www.ankolpakov.ru/
2. «Схема Горнера » Е.А.Максименко, Южный федеральный университет, 2007 г.
3. Исторические сведения: ВИКИПЕДИЯ
.

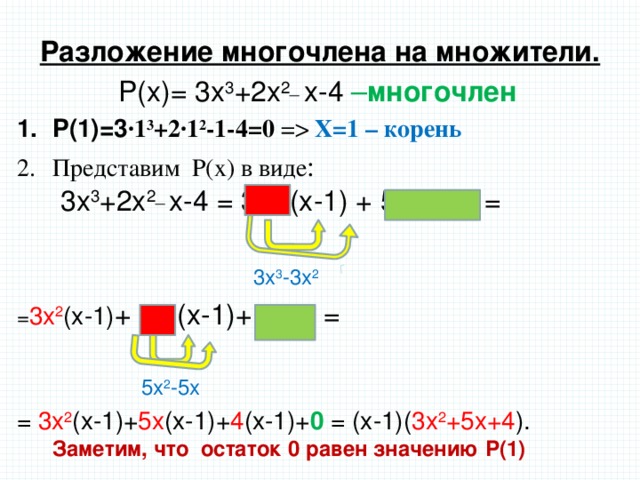 X=1 – корень Представим P(x) в виде : 3x 3 +2x 2_ x-4 = 3x 2 (x-1) + 5x 2 -x-4 = 3x 3 -3x 2 = 3x 2 (x-1) + 5x (x-1)+ 4x-4 = 5x 2 -5x = 3x 2 (x-1)+ 5x (x-1)+ 4 (x-1)+ 0 = (x-1)( 3x 2 +5x+4 ). Заметим, что остаток 0 равен значению Р(1)" width="640"
X=1 – корень Представим P(x) в виде : 3x 3 +2x 2_ x-4 = 3x 2 (x-1) + 5x 2 -x-4 = 3x 3 -3x 2 = 3x 2 (x-1) + 5x (x-1)+ 4x-4 = 5x 2 -5x = 3x 2 (x-1)+ 5x (x-1)+ 4 (x-1)+ 0 = (x-1)( 3x 2 +5x+4 ). Заметим, что остаток 0 равен значению Р(1)" width="640"