Презентация предназначена для урока формирования новых знаний по теме "Показательные неравенства". Содержит основной теоретический материал для актуализации знаний и умений по темам "Показательная функция", "Показательные уравнения". Отражены основные теоретические сведения по новой теме, приведены примеры, а также даны задания для закрепления полученных знаний. Содержит занимательный момент и элемент рефлексии.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Презентация для урока "Показательные уравнения и неравенства"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация для урока "Показательные уравнения и неравенства"»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2020 руб.
2880 руб.
1970 руб.
2820 руб.
2220 руб.
3170 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства






 1 Основание больше нуля и меньше единицы 0 а" width="640"
1 Основание больше нуля и меньше единицы 0 а" width="640"
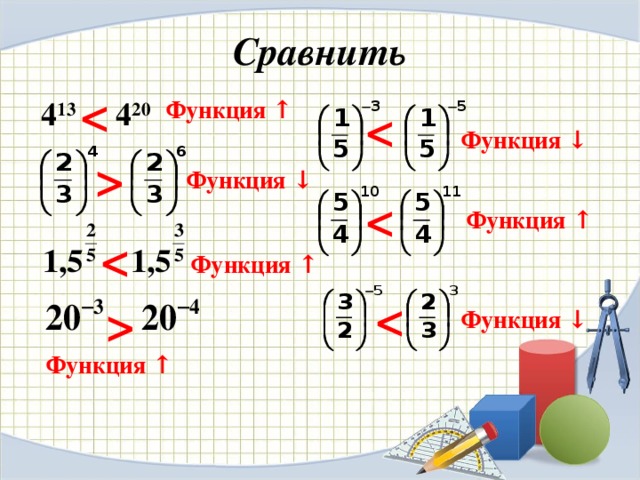 Функция ↓ Функция ↑ Функция ↑ Функция ↓ Функция ↑" width="640"
Функция ↓ Функция ↑ Функция ↑ Функция ↓ Функция ↑" width="640"
 1 функция возрастает При а 1 функция возрастаетП При 0 а функция убывает" width="640"
1 функция возрастает При а 1 функция возрастаетП При 0 а функция убывает" width="640"


 0, a 1, b – любое число ." width="640"
0, a 1, b – любое число ." width="640"




 1 , ф-ция ↑" width="640"
1 , ф-ция ↑" width="640"
 1 , то ф- ция ↑ Ответ: 0 х 2 ." width="640"
1 , то ф- ция ↑ Ответ: 0 х 2 ." width="640"

 1 ф-ия ↑ Ответ : x x 4 x 2" width="640"
1 ф-ия ↑ Ответ : x x 4 x 2" width="640"
 1 ф-ия ↑ Решите неравенство x -5 -5" width="640"
1 ф-ия ↑ Решите неравенство x -5 -5" width="640"
 1 ф-ия ↑ Решите неравенство _ х 1 = 2 х 2 = 3 + + 3 2 Ответ :" width="640"
1 ф-ия ↑ Решите неравенство _ х 1 = 2 х 2 = 3 + + 3 2 Ответ :" width="640"
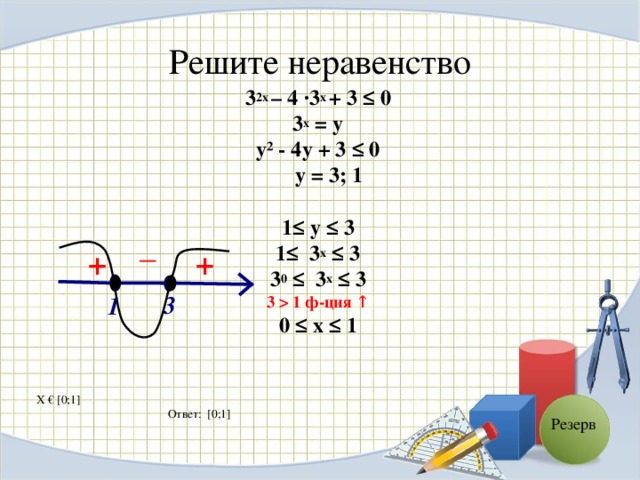 1 ф-ция ↑ 0 ≤ х ≤ 1 Х € [ 0;1 ] Ответ: [ 0;1 ] _ + + 3 1 Резерв" width="640"
1 ф-ция ↑ 0 ≤ х ≤ 1 Х € [ 0;1 ] Ответ: [ 0;1 ] _ + + 3 1 Резерв" width="640"























