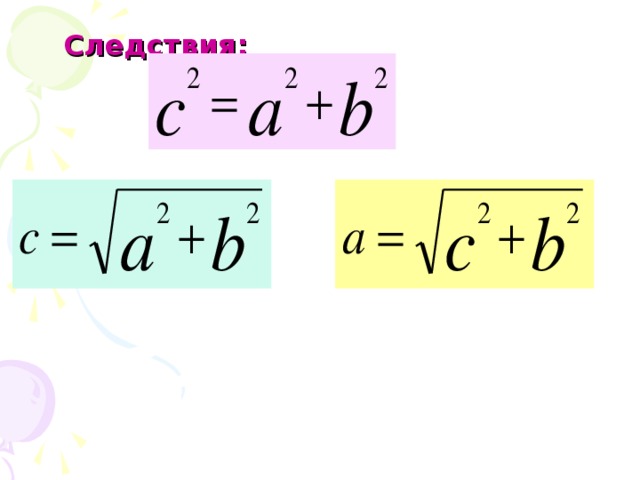Автор разработки: Белянина Светлана Игоревна, учитель математики высшей категории
МБОУ СОШ № 48 города Нижнего Новгорода
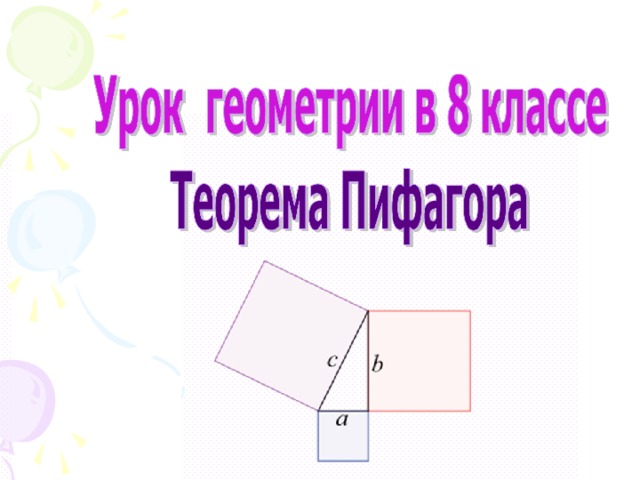
?Тема урока: Теорема Пифагора
?Класс: 8 .Предмет : Геометрия
?Форма проведения: Урок объяснения нового материала ( с использованием презентации)
?Цели и задачи:
Образовательные:
• познакомить учащихся с основными этапами жизни и деятельности Пифагора;
• обеспечить понимание доказательства теоремы Пифагора и ее применение к решению задач.
Развивающие:
• поставить учащихся перед необходимостью получения новых знаний,
• показать, что новые знания могут быть следствием ранее изученной закономерности и развивать математическую речь, умение рассуждать, сравнивать, делать выводы.
• приобрести навыки исследовательской деятельности
• развивать умение работать в сотрудничестве и с учителем
• расширить кругозор учащихся, их познавательный интерес и творческую активность
Воспитательные:
- Показать математику как интересную науку, со своей историей
• воспитывать аккуратность, умение слушать товарищей и учителя.
?Ход урока
-Здравствуйте, ребята. Каждый новый урок – это повод для удивительных открытий.
Я надеюсь, что мы сегодня с вами на уроке сделаем некоторые открытия и наше сотрудничество сегодня будет конструктивным.
- Эпиграфом к нашему уроку являются следующие слова: «Геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора…» Вы наверное
слышали об этом замечательном учёном. Но почему его открытия сравнивают с «великим сокровищем» ? Постараемся ответить на эти вопросы.
Начнем с устной работы.
- Начнём с устной работы.
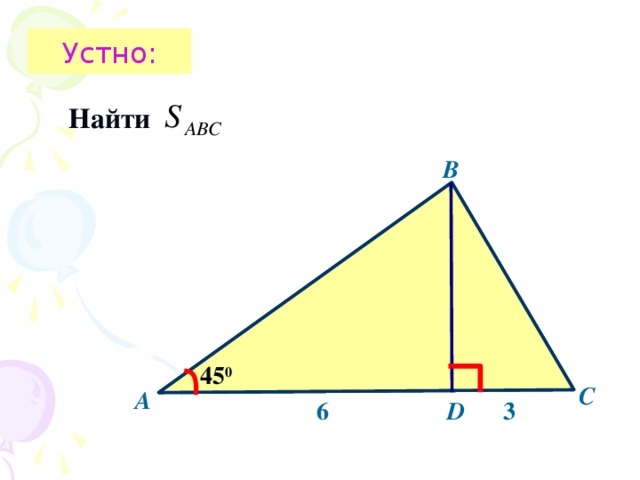
- Найти площадь треугольника, изображённого на рисунке. (смотри слайд 2).
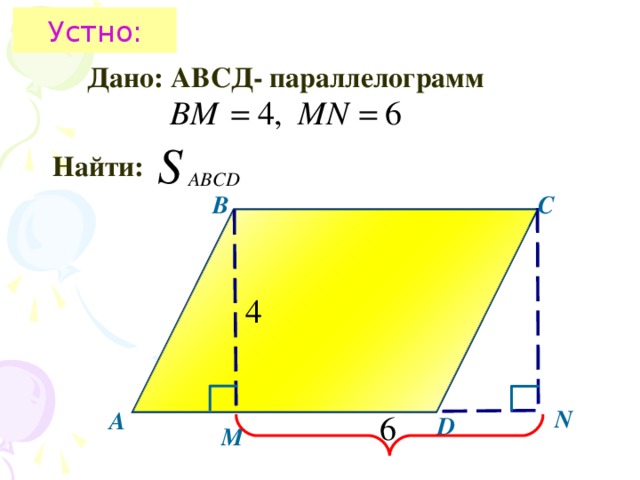
-Найти площадь параллелограмма, изображённого на рисунке. (смотри слайд 3).
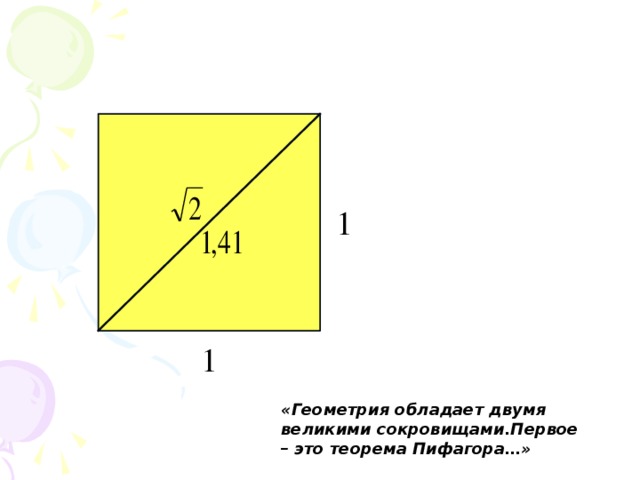
-Найти диагональ квадрата, если сторона квадрата равна 1. (смотри слайд 4)
С древности эта задача считалась неразрешимой. Действительно, в древней Греции в школе учёного Пифагора было сделано открытие несоизмеримости диагонали квадрата с его стороной. И оно считалось одним из ярких достижений древнегреческой математики.
Диагональ квадрата со стороной 1 не выражается рациональным числом. Она равна
иррациональному числу . И ответом на этот вопрос являлась доказанная теорема Пифагора, которая связывает катеты и гипотенузу в прямоугольном треугольнике.
Посмотрим на слайд.
Пифагор (570 – 490 года до н.э.) – древнегреческий математик, философ. Родился Пифагор в Сидоне Финикийском в древней Греции. О его жизненном пути можно судить лишь из произведений других древнегреческих философов. По их мнению, математик Пифагор общался с известнейшими мудрецами, учеными того времени.
Известно, что долгое время Пифагор пробыл в Египте, изучая местные таинства. Затем в биографии философа Пифагора произошла поездка в Вавилон. Лишь после этого он вернулся на Самос. В то время там правил Поликрат, из-за тиранической власти которого Пифагор вынужден был покинуть Самос. Пифагор обосновался на юге Италии. Философия Пифагора, его образ жизни привлекли многих последователей. Сплотившись, они создали школу –Пифагорейский союз. Пифагорейский Союз отличался строгими обычаями и высокой нравственностью. Пифагорейская школа положила начало математическим наукам. В пифагорейской школе начали развиваться астрономия и медицина. Известно, что члены его ордена занимались космологией, верили в переселение душ. (смотри слайды 5-7).
Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров. Ещё Геродот называл его величайшим эллинским мудрецом».
Как математик Пифагор достиг больших успехов. Ему приписывают открытие и доказательство теоремы Пифагора, создание таблицы Пифагора.
Впоследствии стало известно, что теорема , сформулированная Пифагором, была ещё до него доказана в Древней Индии и Древнем Китае, но тем не менее великая теорема носит его имя.
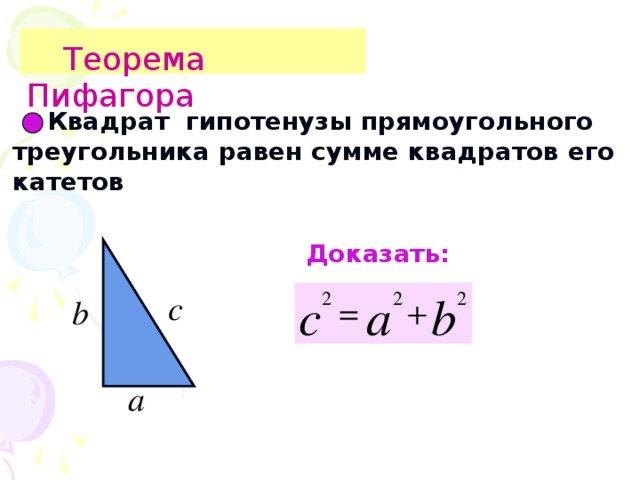
Итак, запишем формулировку теоремы Пифагора.:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
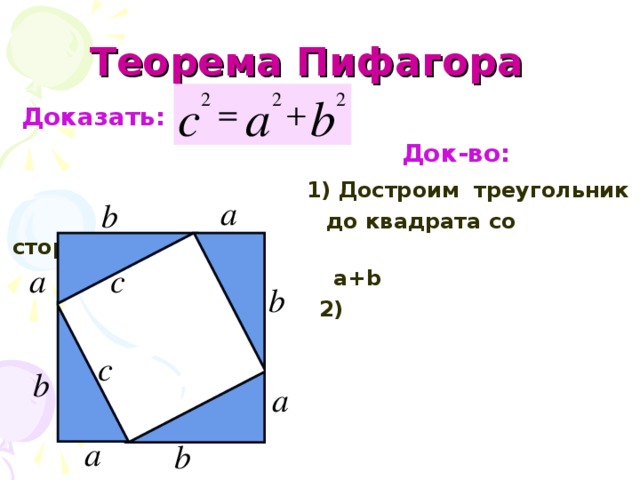
Докажем теорему Пифагора. (См. слайды 8-9).
Очень интересное доказательство. На следующем уроке заслушаем другие доказательства этой замечательной теоремы. (Учитель даёт индивидуальные творческие задания ученикам ).
Запишем основные следствия из теоремы Пифагора(см. слайд 10). Известно много пифагоровых троек : 5,4,3
13,12,5
17, 15, 8
25, 20, 15 и т.д. (Слайд 11)
А теперь рассмотрим основные одношаговые задачи, в которых применяется теорема Пифагора.
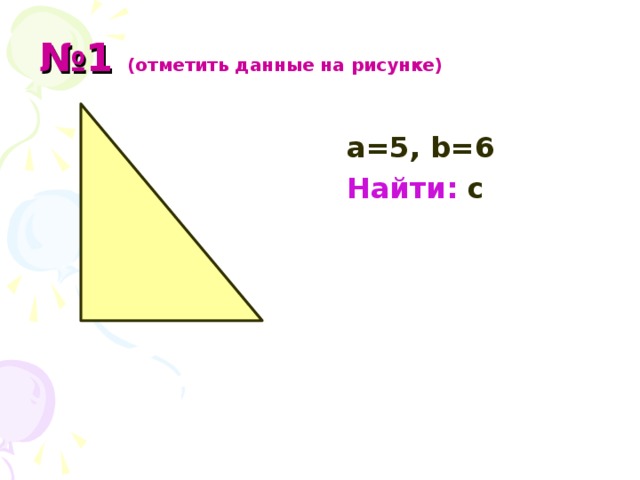
Задача №1. Катеты а и b прямоугольного треугольника равны 5 и 6 соответственно. Найти гипотенузу этого прямоугольного треугольника. Сделаем рисунок, смотри слайд 12.
. Обратите внимание на то, что гипотенуза в этой несложной задаче является иррациональным числом.
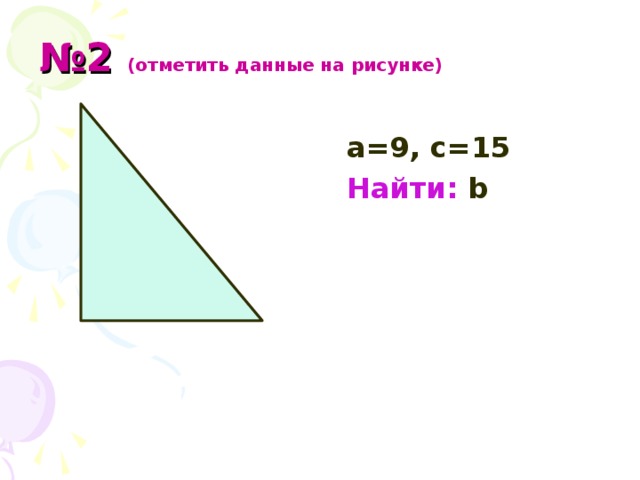
Задача №2 В прямоугольном треугольнике гипотенуза равна 15, а один из катетов 9. Найти длину другой другого катета. (Слайд 13)
Получили ещё одну пифагорову
тройку: 15, 12,9.
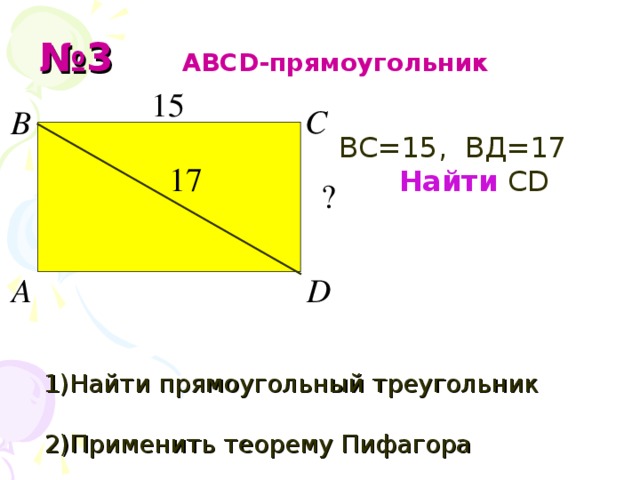
Задача №3. (Слайд № 14, см. ниже). Для решения этой задачи запишем план решения задач с применением теоремы Пифагора. Решим задачу у доски.
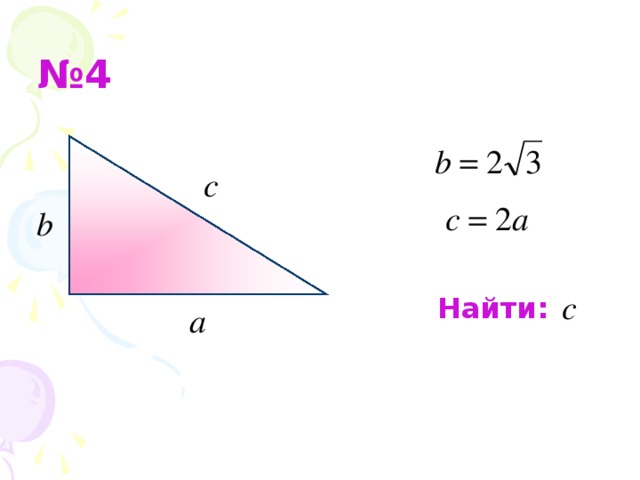
Задача №4 В прямоугольном треугольнике катеты a и b, гипотенуза с. Причём , . Найти с. (Слайд 15). В этой задаче мы составляем уравнение с использованием теоремы Пифагора.
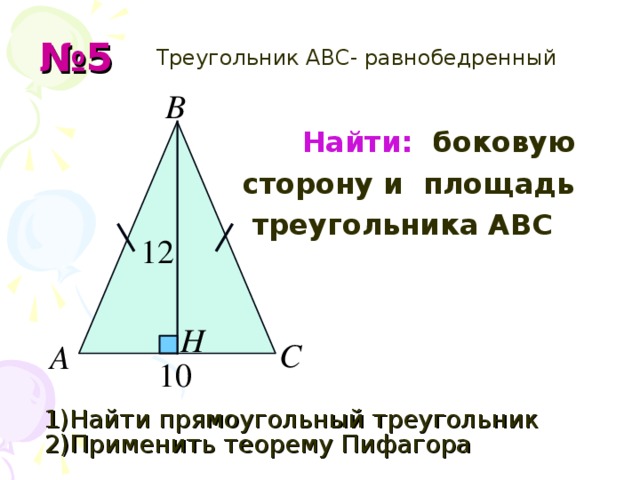
Задача №5 (Слайд 16). Решим задачу 5 у доски
Итак, ребята, мы научились решать основные задачи с использованием теоремы Пифагора.
- Что же узнали мы об этом замечательном учёном, о его теореме?
-Почему её называют «великим сокровищем» геометрической науки.?
- Как вы поняли проблему несоизмеримости диагонали квадрата с его стороной.
На сдедующем уроке мы будем решать более сложные задачи по этой теме, разберём другие доказательства этой великой теоремы.
Запишем домашнее задание:
Выучить Теорема Пифагора, подготовить древнеиндийское, древнекитайское доказательство.
Решить задачи: (задачи раздаются на карточках):
1) Катеты прямоугольного треугольника 6 и 8 см. Найти гипотенузу.( Сделать рисунок)
2) Катеты прямоугольного треугольника
Найти гипотенузу.
3) В прямоугольном треугольнике a и b – катеты, с- гипотенуза.
. Найти катет b.
4)В прямоугольном треугольнике . Найти b.
5) В прямоугольнике АВСД найдите АД, если АВ=5, АС=13
6) Основание равнобедренного треугольника равно 24, а высота, проведённая к основанию, равна 9. Найти боковую сторону.