Построение графиков функций, содержащих переменную под знаком модуля

Построение графиков функций, содержащих переменную под знаком модуля.

г. Мурманск МБОУ гимназия №3

Шахова Татьяна Александровна.

Необходимые умения и навыки.

Уметь решать линейные и

квадратные

неравенства.

http://ta-shah.ucoz.ru/load/8_klass/8_klass/reshenie_kvadratnykh_neravenstv_graficheskim_sposobom/10-1-0-64

Уметь строить графики

элементарных функций.

http://ta-shah.ucoz.ru/load/8_klass/8_klass/postroenie_grafikov_vida_u_f_x_l_m_postroenie_grafika_kvadratichnoj_funkcii/10-1-0-47

Владеть правилами

переноса

графиков.

23.10.23

№ 1 Универсальный способ.

По определению модуля.

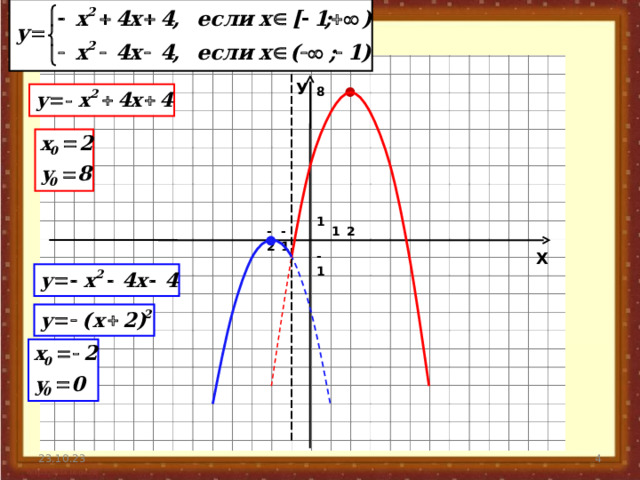
Рассмотрим на конкретном примере.

Построим график функции :

2 случай.

1 случай.

Таким образом :

23.10.23

У

8

1

1

2

-2

-1

-1

Х

23.10.23

Универсальный способ.

По определению модуля.

Алгоритм.

• Сравнить с нулем подмодульные выражения

(решить соответствующие неравенства).

• Аналитически задать функцию на каждом из

полученных числовых промежутков (перейти к

кусочному заданию функции).

3) Построить график полученной кусочной функции.

Замечание: если функция содержит несколько

подмодульных выражений, то удобно для определения

рассматриваемых числовых промежутков использовать

метод интервалов .

Назад

23.10.23

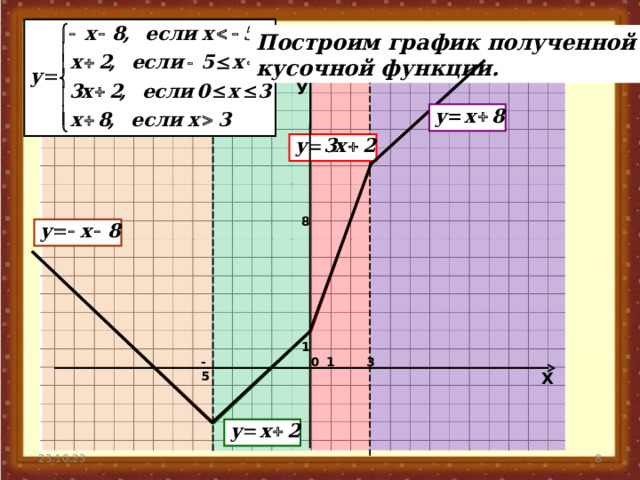
Пример.

Найдем нули подмодульных выражений и разобьем

числовую прямую на интервалы.

Определим знак каждого выражения

на полученных интервалах

Для этого достаточно взять любое число из интервала и

подставить в подмодульные выражения.

23.10.23

Пример.

Теперь можем снять

модули на каждом промежутке.

23.10.23

Построим график полученной

кусочной функции.

У

8

1

3

1

0

-5

Х

23.10.23

Часто график функции, содержащей переменную

под знаком модуля

можно построить быстрее и проще.

Рассмотрим некоторые другие

способы построения.

23.10.23

№ 2 Построение графиков функций вида

f (х)=а 1 |х-х 1 |+а 2 |х-х 2 |+…+а n | x-x n | +ax+b

График - ломаная.

Построим график «методом контрольных точек»

Алгоритм.

• Определить координаты вершин ломаной

( (х 1 ; f(x 1 ) ) , (х 2 ; f(x 2 ) ),….. (х n ; f(x n ) ) ).

• Отметить их в координатной плоскости.

Последовательно соединить отрезками

3) На крайнем левом и крайнем правом промежутке

взять по одной контрольной точке.

• Достроить справа и слева лучи,

проходящие через эти точки

Назад

23.10.23

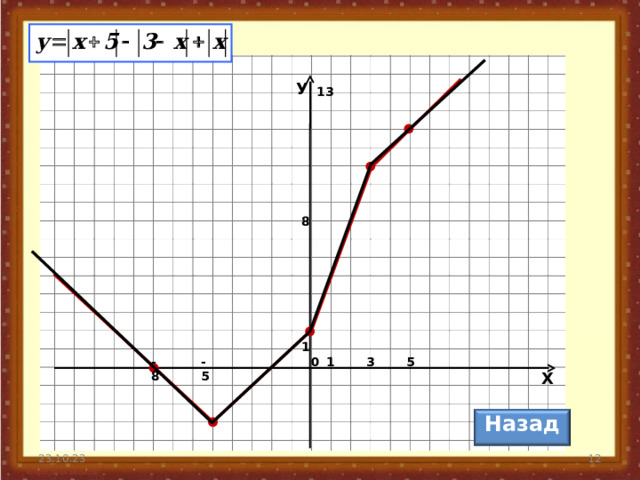
Пример.

• х 1 = -5; у(х 1 )=

|-5+5|-|3-(-5)|+|-5|= -3

(-5;-3)

|3+5|-|3-3|+|3|=12

(3;11)

х 2 = 3; у(х 2 )=

|0+5|-|3-0|+|0|=2

(0;2)

х 3 = 0; у(х 3 )=

Отметим вершины ломаной в координатной плоскости и соединим отрезками.

2)

3) Контрольные точки: х= -8 и х= 5.

(-8;0)

у(-8)=|-8+5|-|3-(-8)|+|-8|= 0

(5;13)

у(5)=|5+5|-|3-5|+|5|= 13

4)

Достроим ломаную.

10

23.10.23

У

13

8

1

3

1

0

-5

5

-8

Х

Назад

23.10.23

11

12

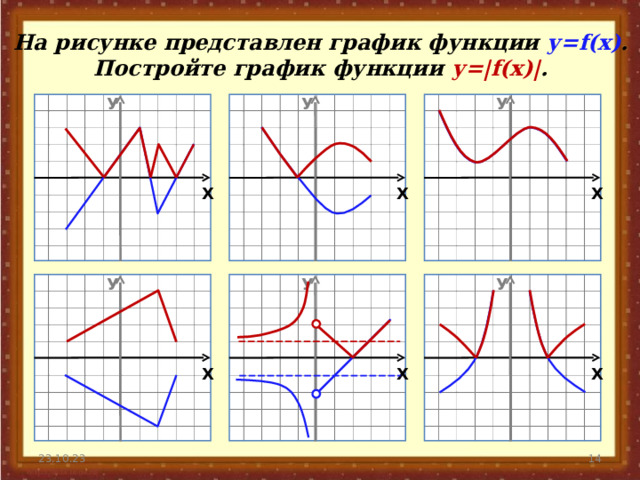
№ 3 Как построить график функции у=| f(x)|,

если известен график функции у= f(x) ?

Очевидно, что для f( х ) ≥ 0 | f( х ) |= f (х) ,

а для f( х ) 0 | f( х ) |= -f (х) .

Алгоритм.

• Построить график функции f(x) .

• Часть полученного графика, лежащую выше Ох

оставить без изменения.

3) Часть полученного графика, лежащую ниже Ох

симметрично отобразить относительно Ох..

Назад

23.10.23

12

На рисунке представлен график функции у= f(x) .

Постройте график функции у=| f(x) | .

У

У

У

Х

Х

Х

У

У

У

Х

Х

Х

13

23.10.23

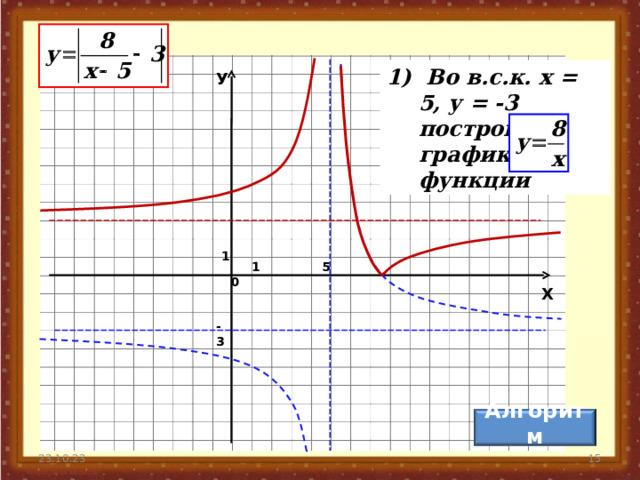
1) Во в.с.к. х = 5, у = -3 построим график функции

У

1

1

5

0

Х

-3

Алгоритм

23.10.23

14

15

№ 4 Как построить график функции у= f(|x|),

если известен график функции у= f(x) ?

Очевидно, что для х ≥ 0 f(| х| ) = f (х) ,

и для х 0 f(| х| ) = f (-х) .

Алгоритм.

• Построить график функции f(x) .

• Оставить только часть полученного графика,

лежащую правее Оу.

• Ее же симметрично отобразить

относительно Оу.

Пример

23.10.23

15

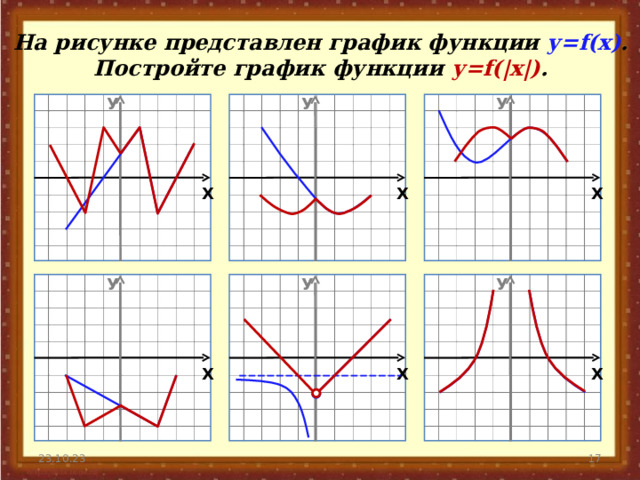
На рисунке представлен график функции у= f(x) .

Постройте график функции у= f(|x|) .

У

У

У

Х

Х

Х

У

У

У

Х

Х

Х

16

23.10.23

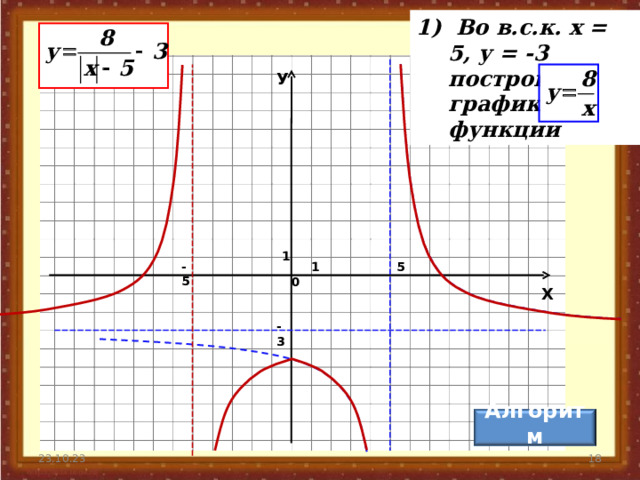
1) Во в.с.к. х = 5, у = -3 построим график функции

У

1

-5

5

1

0

Х

-3

Алгоритм

23.10.23

17

18

№ 5 Как построить график функции у=| f(|x|)|,

если известен график функции у= f(x) ?

Данный график можно построить цепочкой

последовательных преобразований .

Алгоритм.

• Построить график функции f(x) .

2) Построить график

функции | f(x)| .

2) Построить график

функции f(|x| ).

3) Построить график

функции | f(|x|)| .

3) Построить график

функции | f(|x|)| .

Назад

23.10.23

18

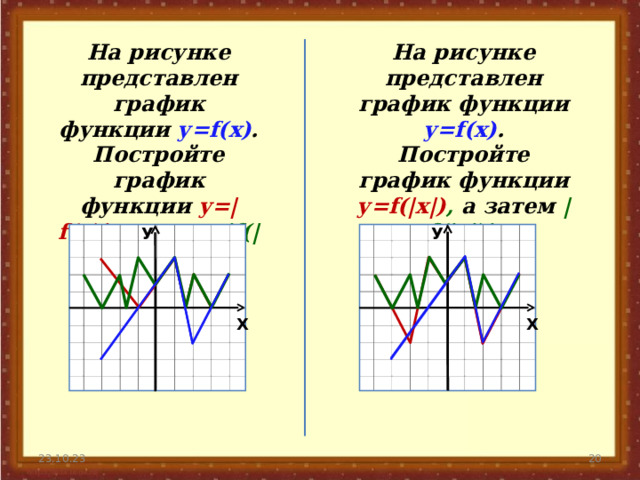
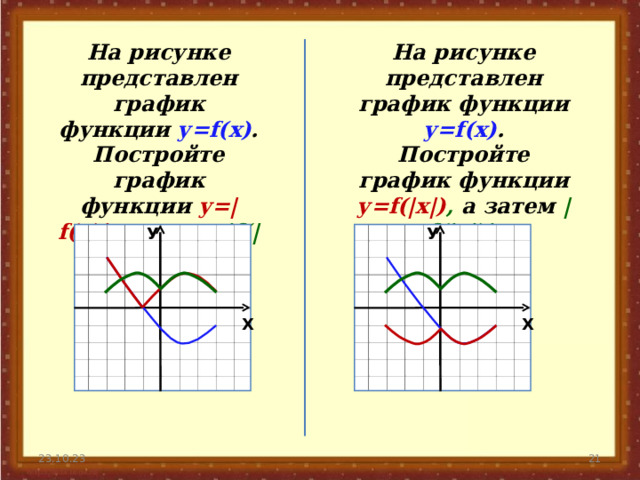
На рисунке представлен график функции у= f(x) .

Постройте график функции у= f(|x|) , а затем | f(|x|)| .

На рисунке представлен график функции у= f(x) .

Постройте график функции у=| f(x)| , а затем | f(|x|)| .

У

У

Х

Х

19

23.10.23

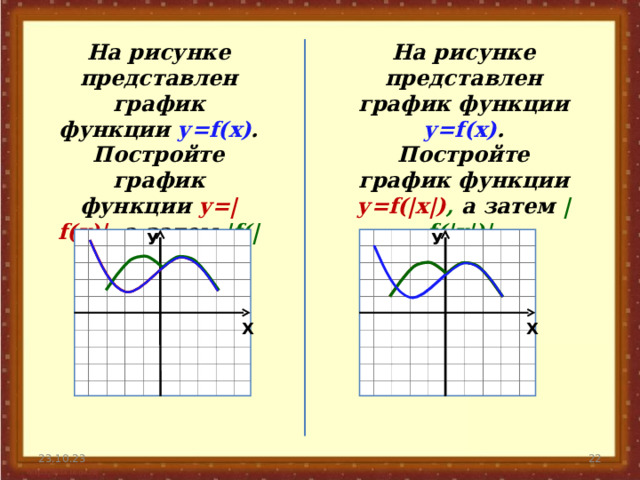
На рисунке представлен график функции у= f(x) .

Постройте график функции у= f(|x|) , а затем | f(|x|)| .

На рисунке представлен график функции у= f(x) .

Постройте график функции у=| f(x)| , а затем | f(|x|)| .

У

У

Х

Х

20

23.10.23

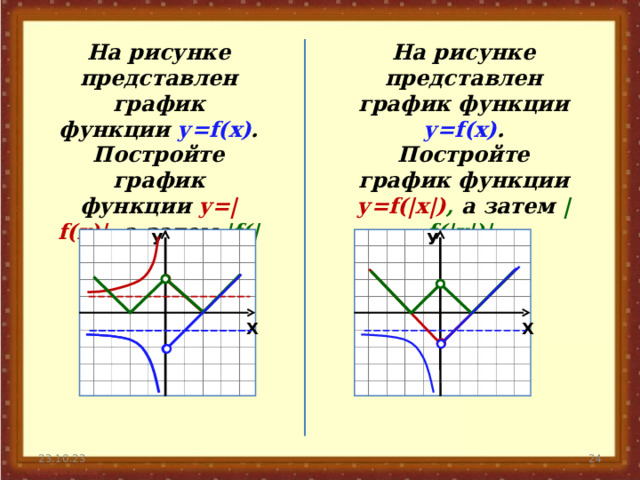
На рисунке представлен график функции у= f(x) .

Постройте график функции у= f(|x|) , а затем | f(|x|)| .

На рисунке представлен график функции у= f(x) .

Постройте график функции у=| f(x)| , а затем | f(|x|)| .

У

У

Х

Х

21

23.10.23

На рисунке представлен график функции у= f(x) .

Постройте график функции у= f(|x|) , а затем | f(|x|)| .

На рисунке представлен график функции у= f(x) .

Постройте график функции у=| f(x)| , а затем | f(|x|)| .

У

У

Х

Х

22

23.10.23

На рисунке представлен график функции у= f(x) .

Постройте график функции у= f(|x|) , а затем | f(|x|)| .

На рисунке представлен график функции у= f(x) .

Постройте график функции у=| f(x)| , а затем | f(|x|)| .

У

У

Х

Х

23

23.10.23

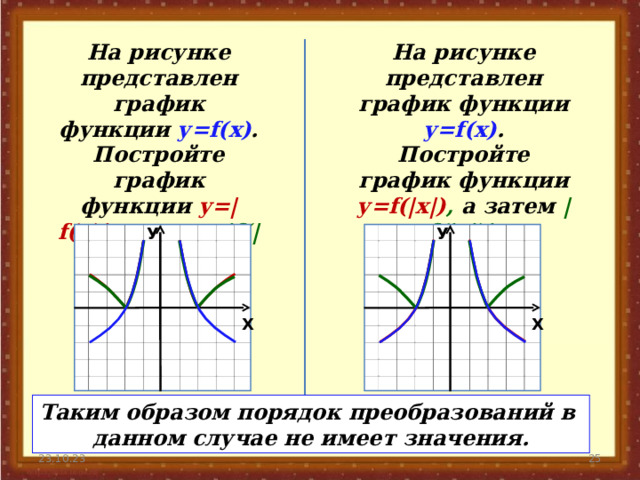
На рисунке представлен график функции у= f(x) .

Постройте график функции у= f(|x|) , а затем | f(|x|)| .

На рисунке представлен график функции у= f(x) .

Постройте график функции у=| f(x)| , а затем | f(|x|)| .

У

У

Х

Х

Таким образом порядок преобразований в

данном случае не имеет значения .

24

23.10.23

Итак, мы рассмотрели 5 способов построения

графиков функций, содержащих переменную

под знаком модуля.

1) Универсальный способ по определению модуля.

2) Метод контрольных точек.

3) Преобразование у= |f(x)| .

4 ) Преобразование у= f(|x|)

5) Цепочка последовательных преобразований.

Способы можно комбинировать.

23.10.23

25

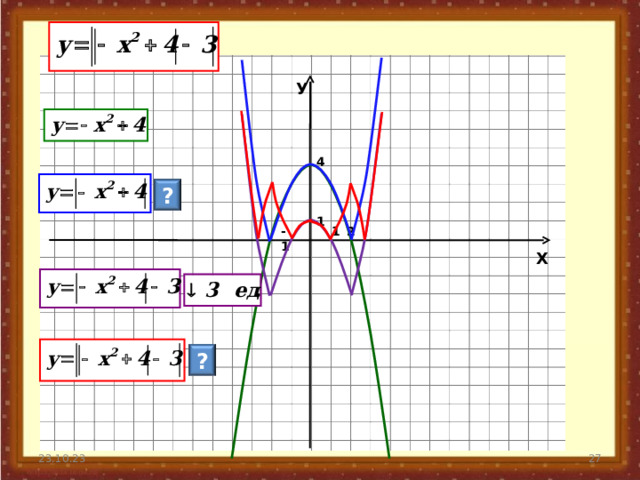
У

4

?

1

-1

2

1

Х

?

23.10.23

26

Определи удобный способ и

построй графики предложенных функций.

Проверить можно в программе геогебра.

http://www.geogebra.org/cms/ru/download/

23.10.23

27