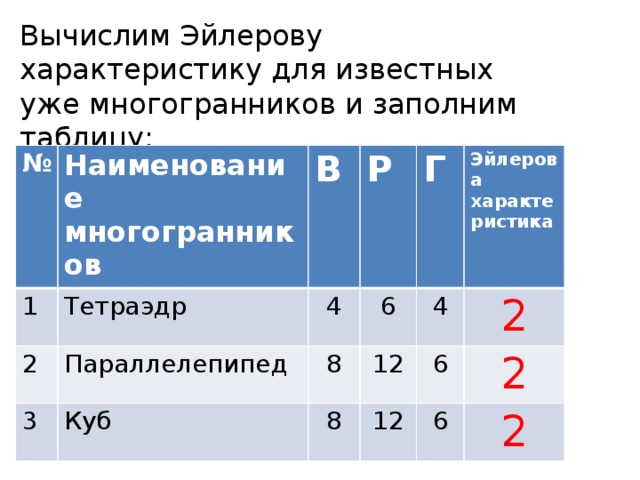
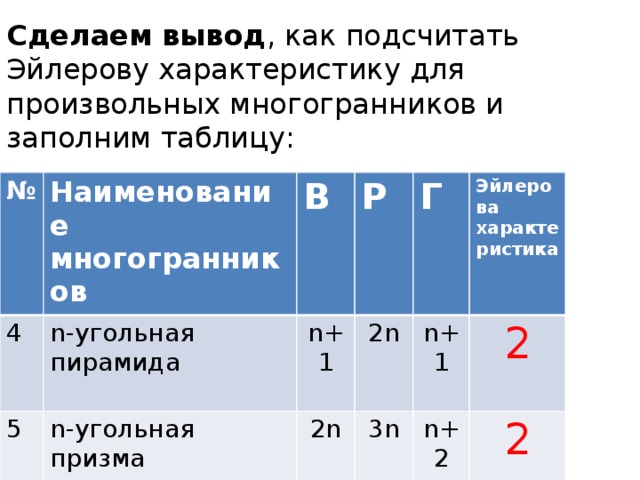
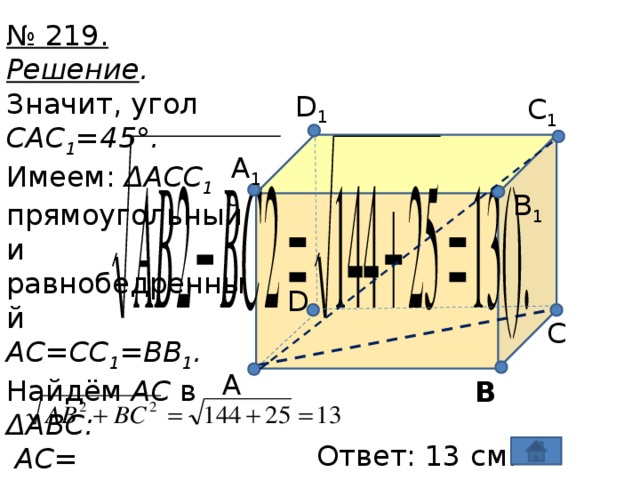
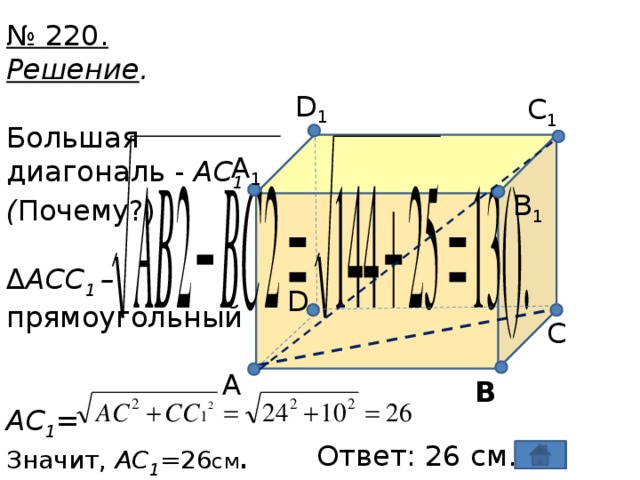
Данная презентация может быть использована при введении темы "Многогранники" на уроках геометрии 10 класса. В презентации рассмотрены определения многогранника, его граней, ребер, вершин, углов, диагоналей, примеры многогранников в жизни и в природе. Приведены формула Эйлера и таблицы с вычисленными характеристиками Эйлера для различных многогранников, которые могут быть использованы для проведения лабораторной работы в классе. А также в презентации приведены решения задач из учебника геометрии 10-11 класса Л. С. Атанасяна, В. Ф. Бутузова и др., предложен вариант домашнего задания.
Файл удален
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
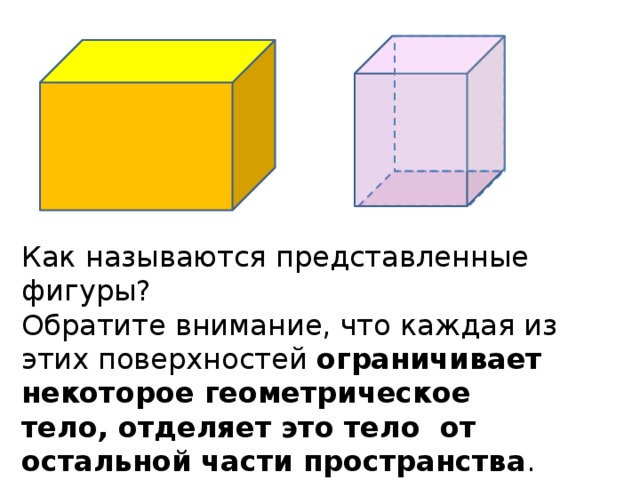
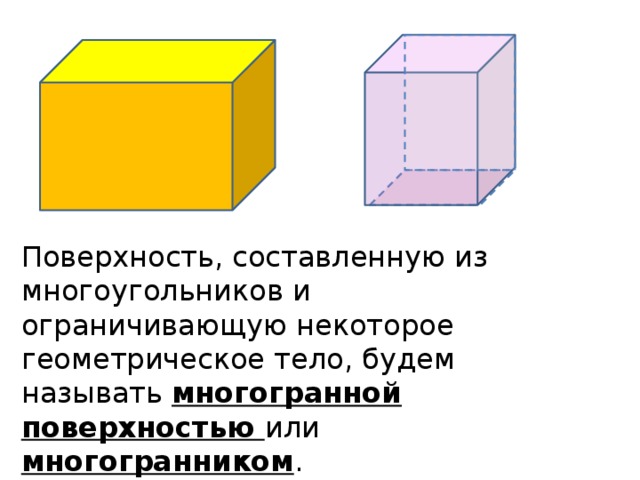
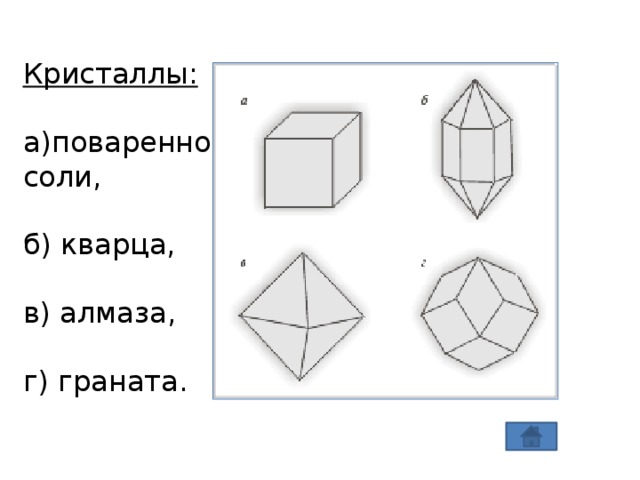
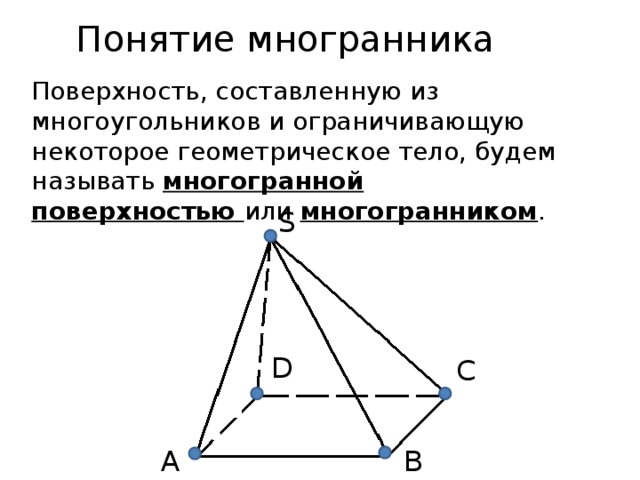
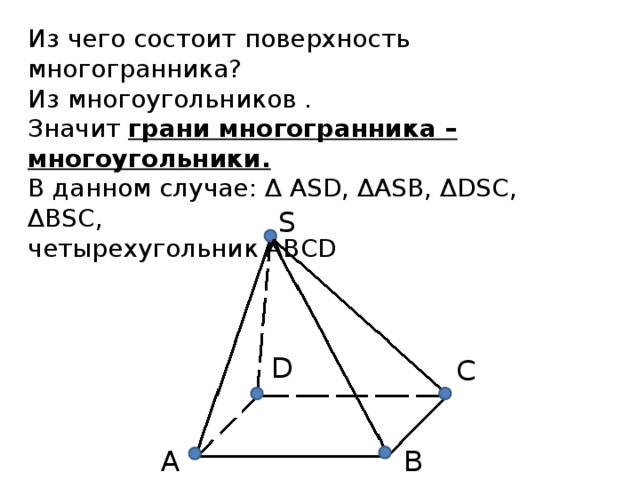
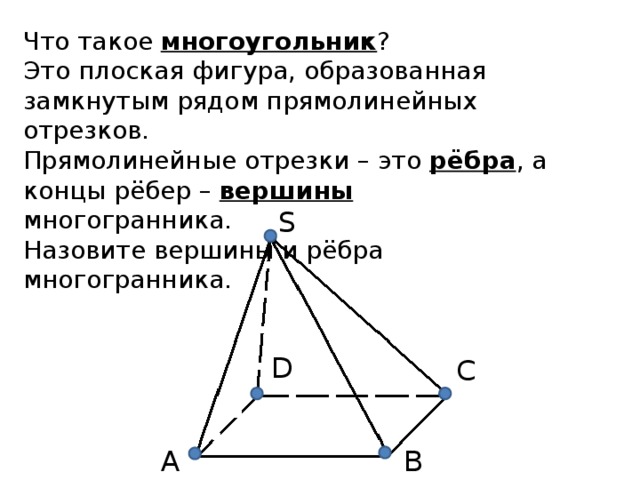
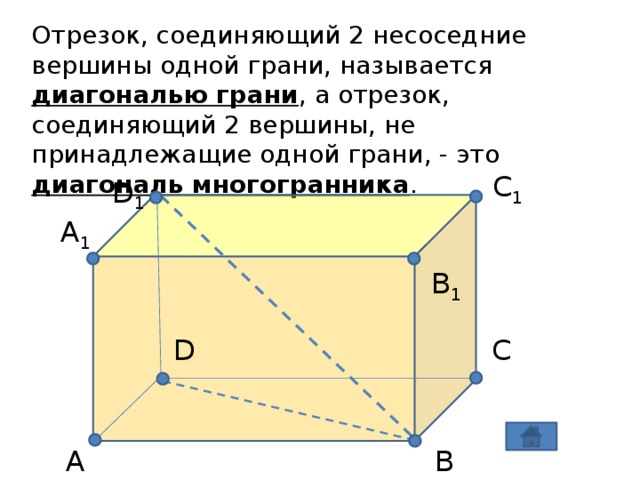
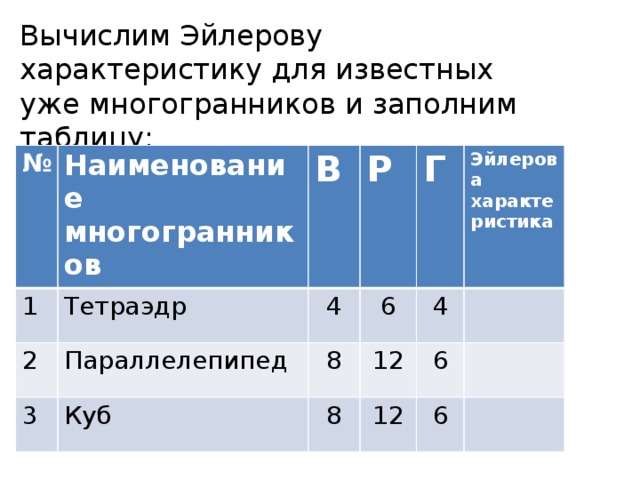
Понятие многогранника
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Понятие многогранника »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1760 руб.
2510 руб.
2020 руб.
2880 руб.
2100 руб.
3000 руб.
1790 руб.
2560 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства