Методическая разработка урока геометрии в 10 классе "Понятие многогранника. Призма"

Данилова А.В.

НЧОУ-лицей «Армавирский классический лицей»

учитель математики.

Методическая разработка урока «Понятие многогранника. Призма». Геометрия 10 класс.

Цели урока.

Образовательные:

• ввести понятие многогранника;

• дать определение призмы;

• рассмотреть решения геометрических задач из учебника по теме «Многогранники».

Развивающие:

• развивать пространственное воображение обучающихся;

• формировать умения чётко и ясно излагать свои мысли;

совершенствовать графическую культуру.

Воспитательные:

• воспитывать умение работать с имеющейся информацией в необычной ситуации;

• воспитывать уважение к предмету, умение видеть геометрические задачи в окружающем нас мире.

Тип урока – изучение нового материала.

Форма урока – урок-практикум.

Формы организации учебной деятельности: коллективная, индивидуальная.

Оборудование:

• Компьютер. Мультимедийный проектор.

• Анимационный слайд-фильм. Электронное «Приложение 1», презентация Microsoft PowerPoint.

• «Рабочая тетрадь», листы формата А4 с готовыми чертежами многогранников. «Приложение 2», лист Microsoft Excel.

Оформление доски: Тема и дата урока.

Структура урока

Вид деятельности.	Время
1. Организационный момент. Постановка цели урока.	5
2. Повторение ранее изученного материала (определение параллелепипеда, прямоугольного параллелепипеда, тетраэдра).	7
3. Обьяснение нового материала (введение понятий многогранника, выпуклых и невыпуклых многогранников, призмы, площади полной поверхности призмы и площади ее боковой поверхности).	20
4. Практическая часть.	35
5. Экскурс «Невозможные объекты».	5
6. Постановка домашнего задания.	3
7. Подведение итогов урока.	5

Ход урока.

1. Сообщение темы и цели урока. Демонстрация слайд-фильма.

Слайд-1.

Тема нашего урока «Понятие многогранника. Призма». Сегодня на уроке мы узнаем, что такое многоранник и познакомимся с одним из них, называемым призмой.

1. Повторение ранее изученного материала.

Давайте вспомним, с какими пространственными фигурами мы с вами уже знакомы? (Тетраэдр и параллелепипед)

Слайд-2.

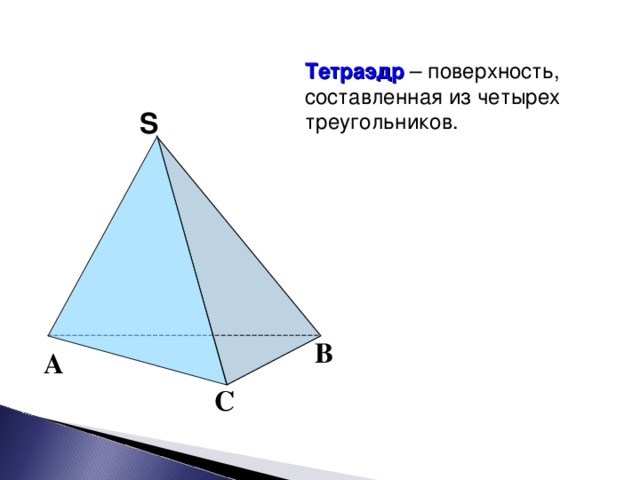
Как вы знаете, тетраэдр-это поверхность, составленная из 4-х треугольников.

(щелчок)

Следующая, известная вам фигура – это параллелепипед.

Слайд-3. (щелчок).

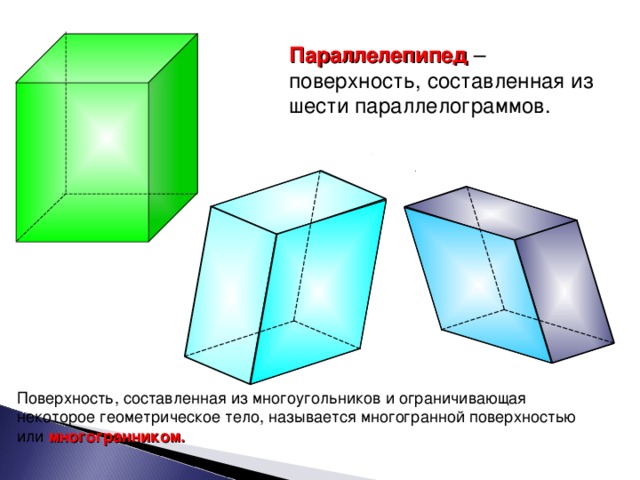
Параллелепипед – это поверхность, составленная из 6-ти параллелограммов. А какой параллелепипед называется прямоугольным?

Т.о. каждая из этих поверхностей ограничивает некоторое геометрическое тело, отделяет это тело от остальной части пространства.

1. Обьяснение нового материала.

Поэтому поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.

(щелчок)

Учащимся предлагается записать определение 1, выведенное на экран.

Слайд-4.

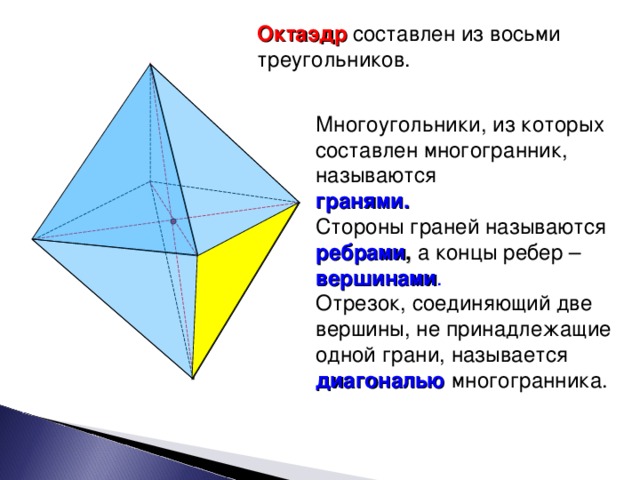
Перед вами еще один пример многогранника – октаэдр, он составлен из 8-ми треугольников.

(щелчок)

Многоугольники, из которых составлен многогранник, называются гранями.

(2 щелчка)

Стороны граней называются ребрами, а концы ребер – вершинами.

(щелчок)

Отрезок, соединяющий 2 вершины, не принадлежащие одной грани, называется диагональю многогранника.

(щелчок)

Многогранники бывают выпуклые и невыпуклые.

Слайд-5.

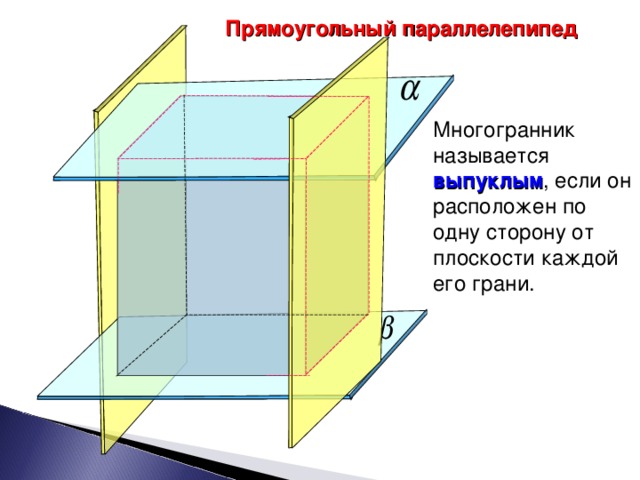
Рассмотрим выпулый многогранник на примере прямоугольного параллелепипеда.

(щелчок)

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Давайте это проверим.

(4 щелчка)

Тетраэдр и октаэдр также являются выпуклыми многогранниками.

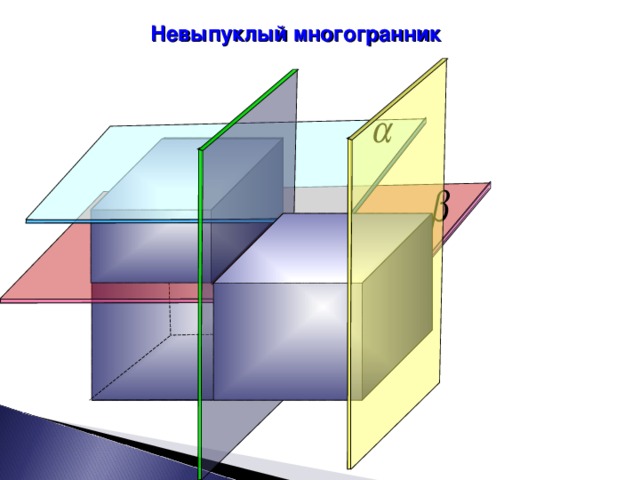
Слайд-6.

Невыпуклый многогранник.

(4 щелчка)

В данном случае не всегда многогранник остается по одну сторону от плоскости грани,он делится на 2 части.

Ясно, что все грани выпуклого многогранника являются выпуклыми многоугольниками.

Также в выпуклом многоугольнике сумма всех плоских углов при каждой его вершине меньше 360º.

Сегодня мы подробно рассмотрим один из многогранников – призму.

Слайд-7.

Перед вами изображена призма. Как вы думаете данная фигура выпуклая или невыпуклая?

(щелчок)

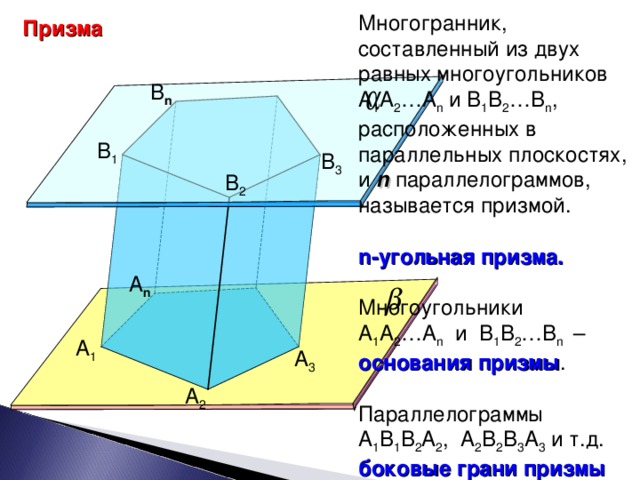
Запишем определение 2 n-угольной призмы.

(щелчок)

Многогранник, составленный из 2-х равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.

(щелчок)

Многоугольники А1А2…Аn и В1В2…Вn – основания призмы.

(щелчок)

Параллелограммы А1В1В2А2 и А2В2В3А3 и т.д. – боковые грани призмы.

Какая из знакомых вам пространственных фигур является призмой?

Слайд-8. (щелчок)

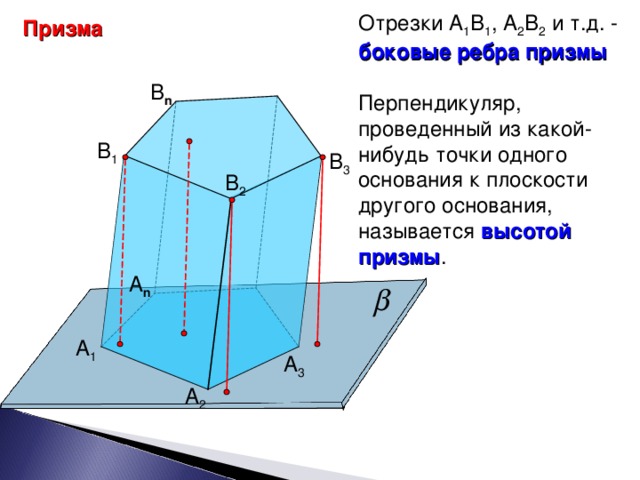
Отрезки А1В1, А2В2 и т.д. – боковые ребра призмы. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется высотой призмы.

(2 щелчка)

Слайд-9.

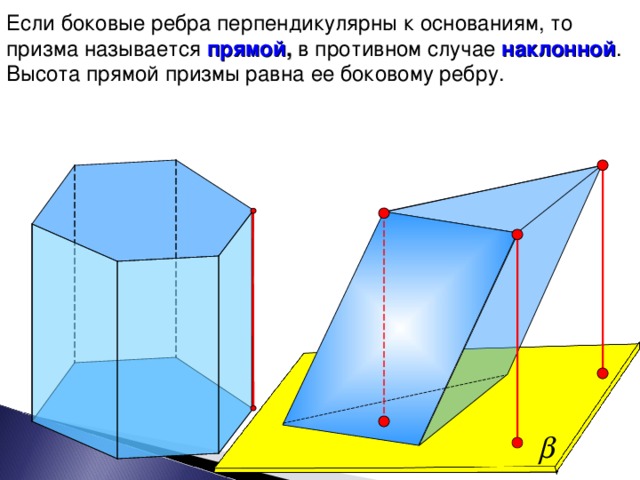
Если боковые ребра перпендикулярны к основанию, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.

(3 щелчка)

Слайд-10.

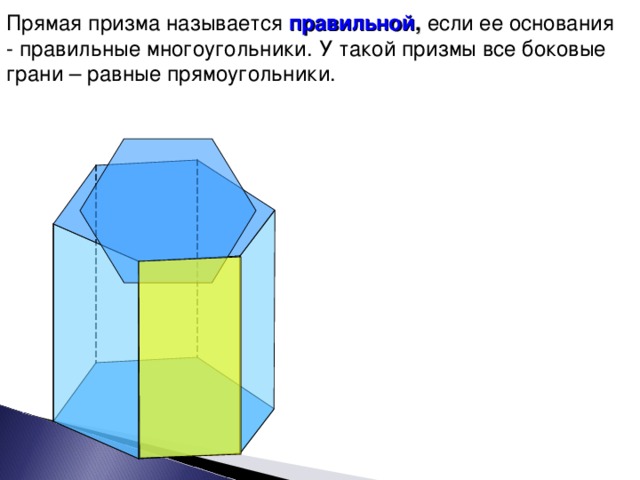
Прямая призма называется правильной, если ее основания – правильные многоугольники. У такой призмы все боковые грани – равные прчмоугольники.

Слайд -11.

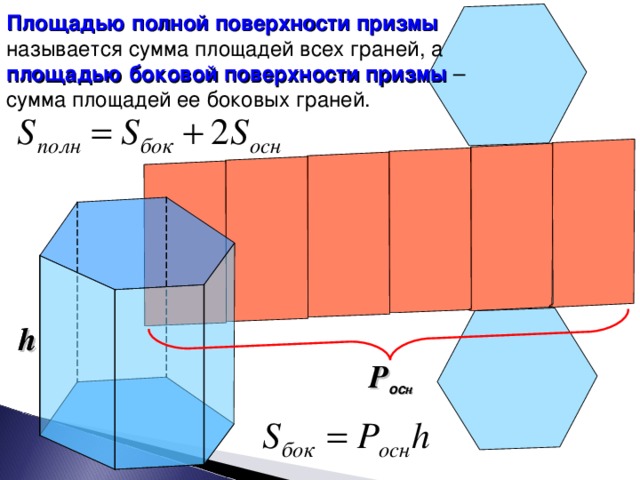
Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой – сумма площадей ее боковых граней.

(щелчок)

Запишите формулу нахождения площади полной поверхности призмы.

(4 щелчка)

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы. Запишите эту формулу.

1. Практическая часть.

На доске записываются номера заданий:

С. 60-61, №219, №221, №222, №223, №230, №231.

Берем рабочие тетради.

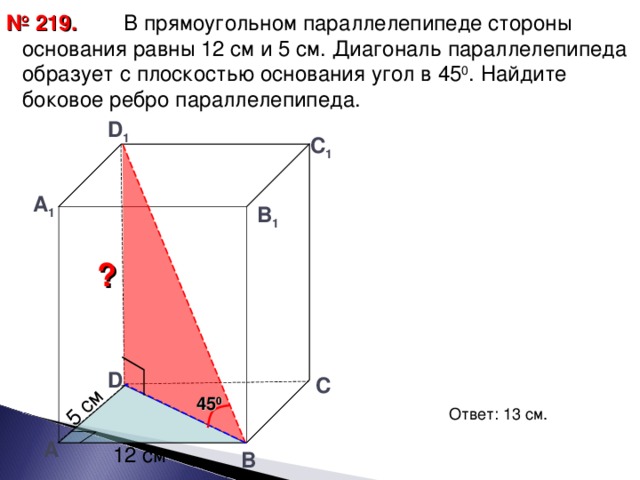
№219. Читаем условие задачи.

Слайд-12

На доске записываем

Дано:АВСДА1В1С1Д1-параллелепипед, АВ=12 см, АД=5 см, ВД1-диагональ.

(щелчок ) Угол ДВД1=45º. Найти: ДД1(щелчок )

Решение:

1. В треугольнике ДД1В: угД=90º (щелчок)

Т.к. угВ=45º, то ДД1=ДВ.

2. Рассмотрим трАДВ (щелчок)

Уг А=90º (щелчок)

АД=5 см, АВ=12см.⇒ ДВ=13см (по Т.Пифагора).

1. Из 1. и 2. ⇒ ДД1=13 см (щелчок)

Ответ: 13 см. (щелчок)

Переходим к следующей задаче.

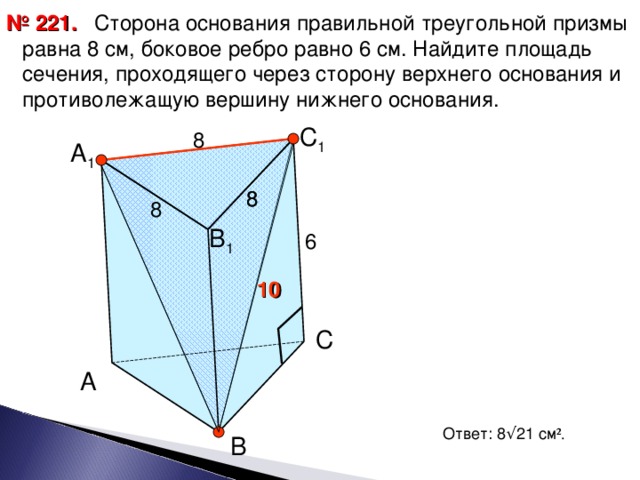
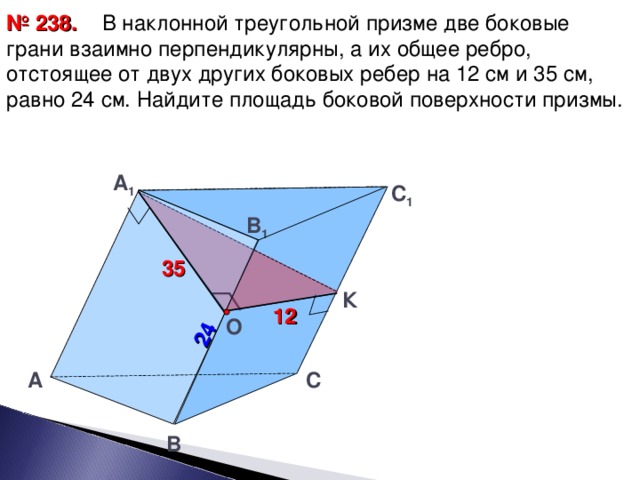
№221. Читаем условие задачи.

Слайд-13

На доске записываем

Дано:АВСА1В1С1- треугольная призма, А1В1=В1С1=А1С1=8 см, СС1=6 см,

Строим сечение (щелчок)

Найти: S трА1С1В.

Решение:

1. Рассмотрим тр ВСС1: СС1=6 см, ВС=8 см (щелчок)

угС=90º (щелчок)

ВС1=10 см (по Т.Пифагора). (щелчок)

1. А1В=ВС1=10 см.

2. S трА1С1В= ф-ла Герона. p=0,5(10+10+8)=14 см. , S= 8√21 см².

Ответ: 8√21 см². (щелчок)

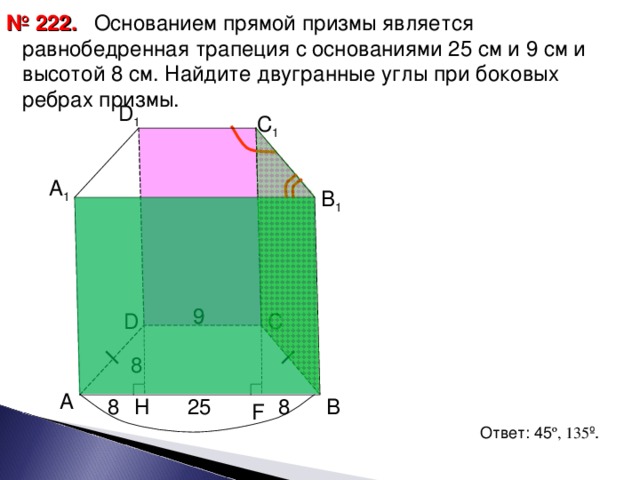
№222. Читаем условие задачи.

Слайд-14

На доске записываем

Дано:АВСДА1В1С1Д1- прямая призма, АВСД-трапеция, АД=СВ, АВ=25 см, ДН｣АВ, ДН=8 см. Найти: (2 щелчка).

Уг А1В1С1 и (3 щелчка).

Уг Д1С1В1.

Решение:

1. Проведем CF｣АВ (2 щелчка).

НF=ДС=9 см (щелчок)

2. АН=FВ= (25-9)/2=8 см (щелчок)

3. Т.к. в трАДС угН=90º, АН=ДН, то уг ДАН=45º.⇒ уг А!В1С1=45º.

4. Уг Д1С1В1=90º+45º=135º.

Ответ: 45º, 135º. (щелчок)

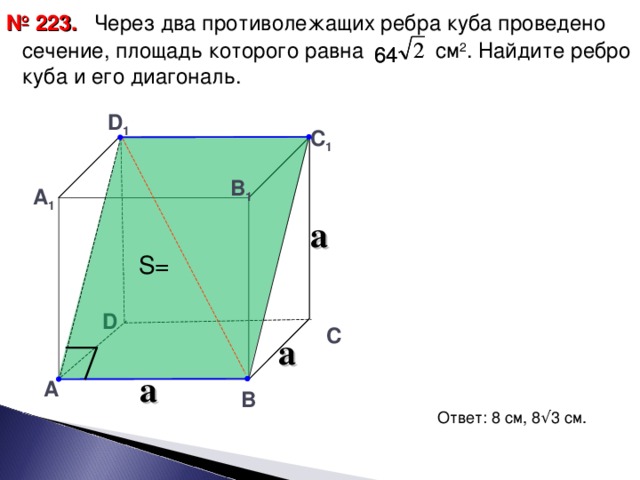
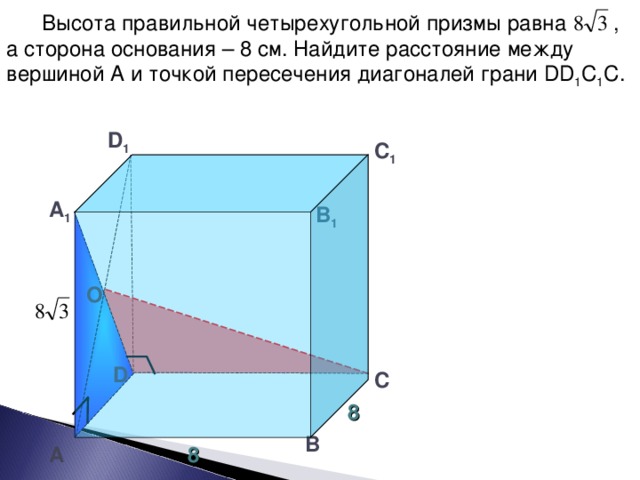
№223. Читаем условие задачи.

Слайд-15

На доске записываем

Дано:АВСДА1В1С1Д1-куб, S АВС1Д1=64 см² (щелчок)

Найти: АВ и ВД1.

Решение:

1. АВС1Д1-прямоугольник. (3 щелчка)

АВ=ВС=СС1=а.

1. В тр ВСС1: угС=90º , ВС=СС1=а, ВС1=а.

2. Т.о. S= а* а,т.е. 64=а² ⇒ а=8 см.

3. В трД1ВА: угА=90º, АВ=8 см, АД1=8  ⇒ ВД1=8√3 см (по Т.Пифагора).

Ответ: 8 см, 8√3 см.

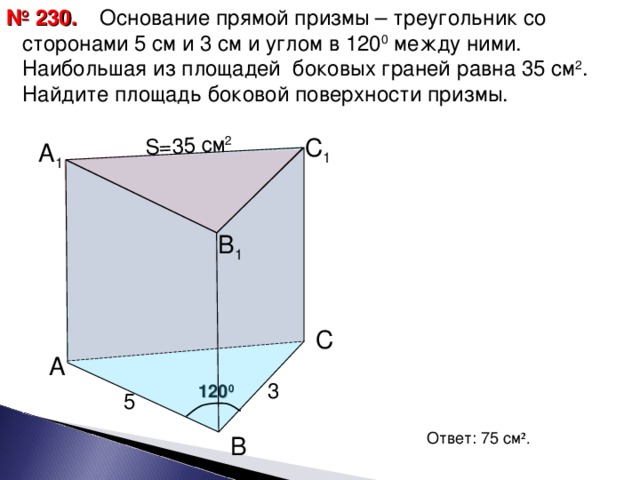
№230. Читаем условие задачи.

Слайд-16

На доске записываем

Дано:АВСА1В1С1- прямая призма, АВ=5 см, ВС=3 см, уг АВС=120º, S АСС1А1=35 см².

(щелчок)

Найти: S бок.

Решение:

1. Sбок=Р*h/

2. По Т.Косинусов: АС²=25+9-2*5*3*cos 120º=49 см².⇒ АС=7 см.

3. АА1=35/7=5 см, Р=5+3+7=15 см.

4. S бок=15*5=75 см².

Ответ: 75 см². (щелчок)

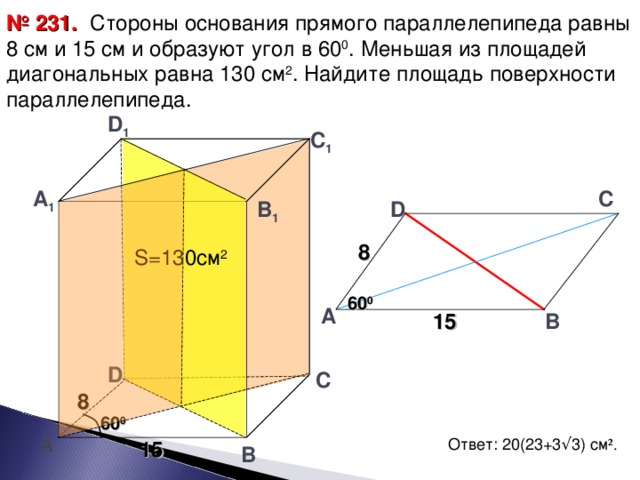
№231. Читаем условие задачи.

Слайд-17

На доске записываем

Дано:АВСДА1В1С1Д1-прямой параллелепипед,АД=8 см, =15 см, уг ДАВ=60º, S ДД1В1В=130 см² (2 щелчка)

Найти: S полн.

Решение:

S полн=S бок+2Sосн.

1. Sосн=2S тр АДВ. По Т.Косинусов: ДВ²=64+225-2*8*15*0,5=169, ДВ=13см.

р=0,5(8+15+13)=18 см, S тр=30√3 см² ( по ф-ле Герона).

S осн=60√3 см².

2. S бок=Росн*h.

Росн=2(*+15)=46 см., h=130/13=10 см.

S бок=46*10=460 см².

3. S полн=460+120√3=20(23+6√3) см². (щелчок)

Ответ: 20(23+6√3) см².

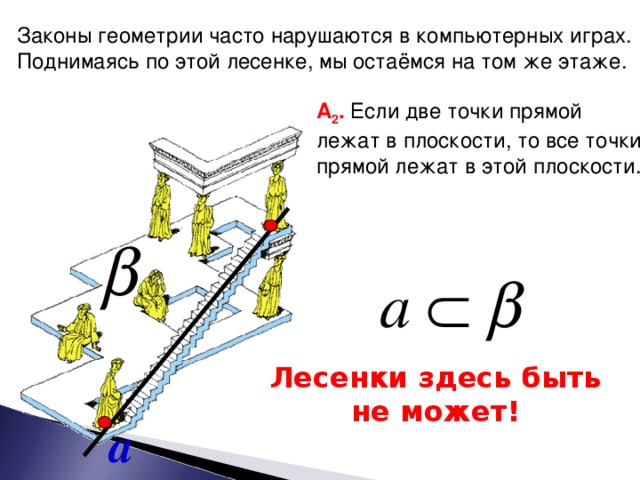
5. Экскурс «Невозможные обьекты».

.

	Слайд-18. Многие художники, искажая законы перспективы, рисуют необычные картины. Эти рисунки очень популярны среди математиков. В сети Internet можно найти множество сайтов, где публикуются эти невозможные объекты. Слайд-19. (щелчок на значок)
Популярные художники Морис Эшер, Оскар Реутерсвард, Жос де Мей удивляли своими картинами математиков. На картине нарушена аксиома А3. Чтобы исправить рисунок сделайте клик на клавише «сведения». Слайд 20. Законы геометрии часто нарушаются в компьютерных играх. Например, встречаются «невозможные лестницы». (2 щелчка) Нарушена аксиома A2.

1. Постановка домашнего задания.

Слайд 21.

7. Подведение итогов урока.

Список литературы:

1. Геометрия: Учеб. Для 10-11 кл. общеобразов. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 9-е изд., с изм. – М.: Просвещение, 2000. – 206 с.:ил. – ISBN 5-09-008612-5.

2. Зив Б.Г. Дидактические материалы по геометрии для 10 класса. – 2-е изд. – М.: Просвещение, 1997. – 144 с.: ISBN 5-09-007468-2.

3. Справочное пособие по методам решения задач по математике для средней школы. Цыпкин А.Г, Пинский А.И./Под. редакцией В.И.Благодатских . – М.: Наука. Главная редакция физико-математической литературы, 1983. – 416 с.

4. Александров А.Д. и др. Геометрия для 10-11 классов: Учеб. пособие для учащихся шк. и классов с углуб. изуч. Математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик.– 4-е изд., перераб. – М.: Просвещение, 1994. – 464 с.: ил.– ISBN 5-09-006089-4

5. Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Часть 3. – М.: «Баласс», «С-инфо», 2002. – 176 с., ил. – ISBN 5-85939-301-6 («Баласс») ISBN 5-85429-031-6 («С-инфо»)

Сайты Internet.

http://alone.sammit.kiev.ua/moremind/illusion/index.html

http://www.im-possible.info/english/art/mey/mey2.html

http://lib.world-mobile.net/culture/special/imp/imp-world-r.narod.ru/art/index.html

http://www.edu.yar.ru/russian/pedbank/sor_uch/math/legcosh/work.html

http://schools.techno.ru/sch758/2004/geometr/a.htm

Л.С. Атанасян. Геометрия 10-11.

Тетраэдр – поверхность, составленная из четырех треугольников.

S

S

В

А

С

2

Параллелепипед – поверхность, составленная из шести параллелограммов.

Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется многогранной поверхностью или многогранником.

3

Октаэдр составлен из восьми треугольников.

Многоугольники, из которых составлен многогранник, называются

гранями.

Стороны граней называются ребрами , а концы ребер – вершинами .

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

4

Прямоугольный параллелепипед

Многогранник называется выпуклым , если он расположен по одну сторону от плоскости каждой его грани.

5

Невыпуклый многогранник

Г.В. Дорофеев, Л.Г. Петерсон, 6 класс (часть 3 ). № 7 42 ( а)

6

Многогранник, составленный из двух равных многоугольников А 1 А 2 …А n и В 1 В 2 …В n , расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.

n -угольная призма.

Многоугольники

А 1 А 2 …А n и В 1 В 2 …В n – основания призмы .

Параллелограммы А 1 В 1 В 2 А 2 , А 2 В 2 В 3 А 3 и т.д. боковые грани призмы

Призма

B n

B 1

B 3

B 2

А n

А 1

А 3

А 2

7

Отрезки А 1 В 1 , А 2 В 2 и т.д. -

боковые ребра призмы

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы .

Призма

B n

B 1

B 3

B 2

А n

А 1

А 3

А 2

8

Если боковые ребра перпендикулярны к основаниям, то призма называется прямой , в противном случае наклонной .

Высота прямой призмы равна ее боковому ребру.

9

Прямая призма называется правильной , если ее основания - правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

9

Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней.

h

h

P oc н

11

5 см

В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 45 0 . Найдите боковое ребро параллелепипеда.

№ 219.

D 1

С 1

А 1

В 1

?

D

С

45 0

Ответ: 13 см.

А

12 см

В

12

Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.

№ 22 1 .

С 1

8

А 1

8

8

8

В 1

6

10

С

А

Ответ: 8 √ 21 см ² .

В

12

Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых ребрах призмы.

№ 22 2 .

D 1

С 1

А 1

В 1

9

9

С

D

8

А

25

H

8

В

8

F

Ответ: 45 º , 135 º .

14

Через два противолежащих ребра куба проведено

сечение, площадь которого равна см 2 . Найдите ребро куба и его диагональ.

№ 223.

64

64

D 1

С 1

В 1

А 1

a

S=

D

С

a

a

А

В

Ответ: 8 см, 8 √ 3 см.

15

Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 120 0 между ними. Наибольшая из площадей боковых граней равна 35 см 2 . Найдите площадь боковой поверхности призмы.

№ 230.

S= 35 см 2

С 1

А 1

В 1

С

А

3

120 0

5

Ответ: 75 см ² .

В

15

№ 231.

Стороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в 60 0 . Меньшая из площадей диагональных равна 130 см 2 . Найдите площадь поверхности параллелепипеда.

D 1

С 1

А 1

С

В 1

D

8

S= 130см 2

60 0

А

15

В

D

С

8

60 0

А

Ответ: 20(23+3 √ 3) см ² .

15

В

17

Это интересно!

Многие художники, искажая законы перспективы, рисуют необычные картины. Кстати, эти рисунки очень популярны среди математиков. В сети Internet можно найти множество сайтов, где публикуются эти невозможные объекты.

Популярные художники Морис Эшер, Оскар Реутерсвард, Жос де Мей и другие, удивляли своими картинами математиков.

http://www.im-possible.info/english/art/mey/mey2.html

http://alone.sammit.kiev.ua/moremind/illusion/index.html

http://lib.world-mobile.net/culture/special/imp/imp-world-r.narod.ru/art/index.html

18

"Такое может нарисовать только тот, кто делает дизайн, не зная перспективы..."

Жос де Мей

19

Законы геометрии часто нарушаются в компьютерных играх.

Поднимаясь по этой лесенке, мы остаёмся на том же этаже.

А 2 . Если две точки прямой

лежат в плоскости, то все точки

прямой лежат в этой плоскости.

Геометрия: Учеб. Для 10-11 кл. общеобразова. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 9-е изд., с изм. – М.: Просвящение, 2000. – 206 с.:ил. – ISBN 5-09-008612-5.

Лесенки здесь быть не может !

а

19

Глава 3, § 1,п.25,27.

№ 220

№ 225

№ 226

№ 232

19

24

10

Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда 10 см. Найдите большую диагональ параллелепипеда.

№ 220.

С 1

D 1

А 1

В 1

10 см

?

D

С

А

В

19

a 2

Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30 0 . Найдите угол между диагональю и плоскостью основания.

№ 225.

a

D 1

С 1

А 1

В 1

2 a

30 0

D

С

a

?

a

А

В

23

В правильной четырехугольной призме через диагональ основания проведено сечение параллельно диагонали призмы. Найдите площадь сечения, если сторона основания призмы равна 2 см, а ее высота 4 см.

№ 226.

D 1

С 1

А 1

В 1

N

4

С

D

2

O

А

2

В

23

№ 228.

Основанием наклонной призмы АВСА 1 В 1 С 1 является равнобедренный треугольник АВС, в котором АС=АВ=13см, ВС=10см,а боковое ребро призмы образует с плоскостью основания угол в 45 0 . Проекцией вершины А 1 является точка пересечения медиан треугольника АВС. Найдите площадь грани СС 1 В 1 В.

А 1

C 1

B 1

13

А

C

13

10

B

25

№ 2 32 .

Диагональ прямоугольного параллелепипеда, равная d , образует с плоскостью основания угол , а с одной из боковых граней – угол . Найдите площадь боковой поверхности параллелепипеда.

D 1

С 1

А 1

В 1

d

D

С

В

А

26

Основание прямой призмы АВСА 1 В 1 С 1 является прямоугольный треугольник АВС с прямым углом В. Через ребро ВВ 1 проведено сечение ВВ 1 D 1 D , перпендикулярное к

плоскости грани АА 1 С 1 С.

Найдите площадь сечения,

если АА 1 =10см, А D =27см,

DC = 12см.

№ 2 3 3.

В 1

А 1

С 1

D 1

Из АВС

10

S сеч = 10 * 18

В

27

12

С

D

А

27

2 0

21

21

2 0

Основанием прямой призмы является прямоугольный треугольник. Через середину гипотенузы перпендикулярно к ней проведена плоскость. Найдите S сеч ,

если катеты равны 20см и 21см,

а боковое ребро равно 42 см.

№ 2 3 4.

В 1

N 1

А 1

С 1

D 1

В

42

N

В

?

N

А

С

D

D

С

А

28

24

В наклонной треугольной призме две боковые грани взаимно перпендикулярны, а их общее ребро, отстоящее от двух других боковых ребер на 12 см и 35 см, равно 24 см. Найдите площадь боковой поверхности призмы.

№ 23 8 .

А 1

C 1

B 1

35

К

12

О

C

А

B

29

Высота правильной четырехугольной призмы равна , а сторона основания – 8 см. Найдите расстояние между вершиной А и точкой пересечения диагоналей грани DD 1 С 1 С.

D 1

С 1

А 1

В 1

О

Тесты. Геометрия 11 класс. Варианты и ответы централизованного (итогового) тестирования – М.: Центр тестирования МО РФ, 2004.

D

С

8

В

А

8

29