Основные тригонометрические функции

CЛАЙД 1Основные тригонометрические функции Демидова Надежда Алексеевна преподаватель общеобразовательных дисциплин КГБПОУ  «Змеиногорский лицей профессионального образования» Урок – презентация для студентов 1 курса

СЛАЙД 2 Вопросы 

1.Что такое числовая окружность?

2.Что называется косинусом числа t?

3.Что называется синусом числа t?

4.Что называется тангенсом числа t?

5.Что называется котангенсом числа t?

6.Какие функции являются функциями числового аргумента?

7.Какие функции являются функциями углового аргумента?

8.Какие меры измерения  существуют для измерения угла?

СЛАЙД 3 Ответы на вопросы 

1.Числовая окружность – это математическая модель необходимая для введения тригонометрических функций.

2.Косинусом числа t называется абсцисса точки ( х = cos t).

3.Синусом числа t называется ордината точки ( у = sin t).

4.Тангенсом числа t называется отношение синуса числа t к косинусу числа t  ( обозначается tg  t ).

5.Котангенсом числа t называется отношение косинуса числа t к синусу числа t  ( обозначается сtg  t ).

6.Функциями числового аргумента являются функции вида u = sin t,

         u = cos t, u = tg  t , u = сtg  t, где  t  любое действительное число для синуса и косинуса, а для тангенса  t любое действительное число  кроме t = п/2+ пr,  для котангенса t любое действительное число  кроме t = пr,   где r любое целое число.

7.   Функциями углового аргумента являются функции вида  у = sin t, у = cost,  у = tg t,  у = ctg t, где t любое значение угла.

8.     Для измерения угла существуют меры измерения: градусная и радианная. 

СЛАЙД 4 Свойства функции y= cos А и y= sin А

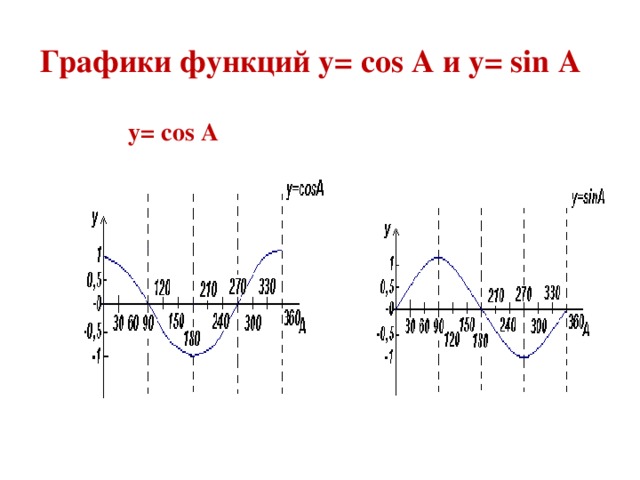
y= cos А

1.D = R

2.Е = [-1;1]

3.cos (-x) = cos x

4.min (y) = -1,

      mas (y) = 1

5.   Т = 2п

6.Непрерывная

7.Выпукла вверх [- п/2;п/2]

 выпукла вниз [п/2;3п/2]

y= sin А

1.D = R

2.Е = [-1;1]

3.sin (-x) = - sin x

4.min (y) = -1,

      mas (y) = 1

5.   Т = 2п

6.Непрерывная

7.Выпукла вверх [0;п], выпукла вниз [п;2п]

СЛАЙД 5 Графики функций y= cos А и y= sin А  

СЛАЙД 6 Свойства функции y= tg x и y= ctg x 

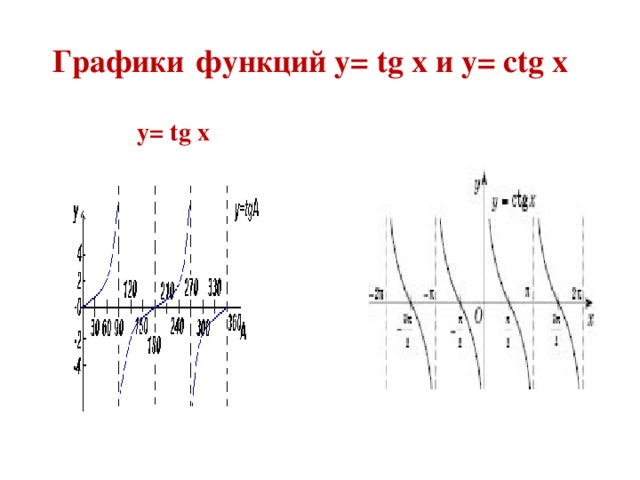
y= tg x

1.D = R кроме

       х= п/2 + пr,

       r принадлежит Z

2.    Е = R

3.    tg (-x) = -tg x

4.   min (y) не имеет

      mas (y) не имеет

5.   Т = п

6.Возрастает [- п/2; п/2]

7.Неограниченная  ни снизу, ни сверху

8. Непрерывная [- п/2; п/2]

y= ctg х

1. D = R кроме х= пr,

        r принадлежит Z

2.     Е = R

3.    ctg (-x) = - ctg x

4.    min (y) не имеет

      mas (y) не имеет

5.   Т = п

6.  Непрерывная [0; п]

7.   Убывает [0; п]

8. Неограниченная  ни снизу, ни сверху

СЛАЙД 7 Графики функций y= tg x и y= ctg x  

СЛАЙД 8 Практические задания

Учебник А. Г. Морткович Алгебра и начала анализа 10, часть 2.   

1.Стр. 77: 13.1, 13.4 (а,б).

2.Стр. 78: 13.14.

3.Стр.  79: 13.16(а;в).  

4.Стр.  83: 14.1, 14.2, 14.5.

5.Стр . 90: 16.1, 16.4.

Стр. 92:  16.11, 16.14.