Немного о геометрии

Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости: треугольники, окружности, параллелограммы и т.д.

Первое систематическое изложение планиметрии впервые было дано Евклидом в его труде «Начала».

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого презентации
«к уроку»

Составитель: Соснина Е.В.,

школа №7

Выход

Первое сочинение, содержащее простейшие геометрические сведения, дошло до нас из Древнего Египта. Оно относится к 17 в. до н. э. В нем содержатся правила вычисления площадей и объемов некоторых фигур и тел. Эти правила были получены практическим путем, без какого-либо логического доказательства их справедливости.

Становление геометрии как математической науки произошло позднее и связано с именами греческих ученых Фалеса (ок. 625— 547 гг. до н. э.), Пифагора (ок. 580—500 гг. до н. э.), Демокрита (ок. 460—370 гг. до н. э.), Евклида (3 в. до н. э.) и др. В знаменитом сочинении Евклида «Начала» были систематизированы основные известные в то время геометрические сведения. Главное же — в «Началах» был развит аксиоматический подход к построению геометрии, который состоит в том, что сначала формулируются основные положения (аксиомы), а затем на их основе посредством рассуждений доказываются другие утверждения (теоремы).

Полученные результаты используются как на практике, так и в дальнейших научных исследованиях. Некоторые из аксиом, предложенных Евклидом, и сейчас используются в курсах геометрии. Часть из них в современной формулировке имеется в нашем курсе. Например: «Через любые две точки проходит прямая, и притом только одна».

Большой вклад в дальнейшее исследование различных вопросов геометрии внесли Архимед (ок. 287—212 гг. до н. э.), Аполлоний ( 3 в. до н. э.) и другие дневнегреческие ученые.

Качественно новый этап в развитии геометрии начался лишь много веков спустя — в 17 в. н. э.— и был связан с накопленными к этому времени достижениями алгебры. Выдающийся французский математик и философ Р. Декарт (1596—1650) предложил новый подход к решению геометрических задач. В своей «Геометрии» (1637) он ввел метод координат, связав геометрию и алгебру, что позволило решать многие геометрические задачи алгебраическими методами.

На возможность такого подхода впервые указал греческий ученый Аристотель (ок. 384—322 гг. до н. э.).

В развитии геометрии важную роль сыграла аксиома, которая в «Началах» Евклида называлась пятым постулатом. Формулировка пятого постулата у Евклида весьма сложна. Поэтому обычно его заменяют эквивалентной ему аксиомой параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Много веков усилия большого числа ученых были направлены на доказательство пятого постулата. Это объяснялось тем, что число аксиом стремились свести к минимуму. Ученые думали, что пятый постулат можно доказать как теорему, опираясь на остальные аксиомы.

В конце 18 в. у некоторых геометров возникла мысль о невозможности доказать пятый постулат. Решение этого вопроса было найдено великим русским математиком Николаем Ивановичем Лобачевским (1792—1856).

Вся творческая жизнь нашего выдающегося соотечественника была связана с Казанским университетом, где он учился, затем был профессором, а с 1827 г.— ректором университета. Его очень рано заинтересовала геометрия, и он, как и многие его предшественники, пытался доказать пятый постулат Евклида. Лобачевский предпринял попытку доказать пятый постулат от противного: он предположил, что через данную точку, не лежащую на данной прямой, можно провести несколько прямых, не пересекающих данную. Исходя из этого, он попытался получить утверждение, которое противоречило бы аксиомам или полученным из них теоремам..

Если бы такое утверждение удалось получить, то это означало бы, что предположение неверно, а верно противоположное утверждение: через точку, не лежащую на данной прямой, можно провести только одну прямую, не пересекающую данную. Тем самым пятый постулат Евклида был бы доказан.

Но Лобачевский не получил противоречивых утверждений. На основании этого им был сделан замечательный вывод: можно построить другую геометрию, отличную от геометрии Евклида. Такая геометрия им была построена. Ее называют теперь геометрией Лобачевского. Сообщение об открытии новой геометрии было сделано Лобачевским в 1826 г.

К аналогичным выводам пришел венгерский математик Я. Бойяи (1802—1860), но он свои результаты опубликовал несколько позже, в 1832 г. В рукописях великого немецкого математика К- Ф. Гаусса (1777—1855) высказывались идеи, близкие к идеям Лобачевского и Бойяи. Однако он, опасаясь критики, не решился их обнародовать.

При изучении геометрии мы опирались на ряд аксиом. Напомним, что аксиомами называются те основные положения геометрии, которые принимаются в качестве исходных. Вместе с так называемыми основными понятиями они образуют фундамент для построения геометрии. Первыми основными понятиями, с которыми мы познакомились, были понятия точки и прямой. Определения основных понятий не даются, а их свойства выражаются в аксиомах. Используя основные понятия и аксиомы, мы даем определения новых понятий, формулируем и доказываем теоремы и таким образом изучаем свойства геометрических фигур.

Отметим, что не все аксиомы, необходимые для построения планиметрии, были приведены в нашем курсе — для упрощения изложения некоторые из них мы не формулировали, хотя ими и пользовались. Здесь мы приведем все аксиомы планиметрии.

Первые три аксиомы характеризуют взаимное расположение точек и прямых.

1. Каждой прямой принадлежат по крайней мере две точки.

Такие понятия, как «принадлежать», «множество», «число» и т. д., относятся не только к геометрии, но и к другим разделам математики. Поэтому мы считаем их известными и не относим к числу основных понятий планиметрии.

2. Имеются по крайней мере три точки, не лежащие на одной прямой.

3. Через любые две точки проходит прямая, и притом только одна.

Для точек, лежащих на одной прямой, мы использовали понятие «лежать между», которое относим к основным понятиям геометрии. Свойство этого понятия выражено в следующей аксиоме:

4. Из трех точек прямой одна и только одна лежит между двумя другими.

Подчеркнем, что, говоря «точка В лежит между точками А и С», мы имеем в виду, что А, В, С — различные точки прямой и точка В лежит также между С и А. Иногда вместо этих слов мы говорим, что точки А и В лежат по одну сторону от точки С (аналогично точки В и С лежат по одну сторону от точки А) или точки А и С лежат по разные стороны от точки В.

5. Каждая точка О прямой разделяет ее на две части (два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.

При этом точка О не принадлежит ни одному из указанных лучей.

Напомним, что отрезком АВ называется геометрическая фигура, состоящая из точек А и В и всех точек прямой АВ лежащих между А и В. Коротко можно сказать так: отрезок -это часть прямой, ограниченная двумя точками. Если отрезок АВ не имеет общих точек с прямой а, то говорят, что точки А и В лежат по одну сторону от прямой а; если же отрезок АВ пересекается с прямой а (в некоторой точке С, лежащей между А и В), то говорят, что точки А и В лежат по разные стороны от прямой а.

6. Каждая прямая а разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.

Прямая а называется границей каждой из указанных полуплоскостей: ее точки не принадлежат ни одной из этих полуплоскостей.

Следующие аксиомы связаны с понятиями наложения и равенства фигур. Понятие наложения относится в нашем курсе к основным понятиям геометрии. Мы определили равенство геометрических фигур, используя понятие наложения. При этом мы опирались на наглядные представления о наложении фигур и допускали, что всякая геометрическая фигура может перемещаться как единое целое, наподобие того, как перемещаются материальные тела. Но геометрические фигуры не материальные тела, а воображаемые объекты, поэтому наложение геометрических фигур следует понимать в особом смысле.

Чтобы выяснить этот смысл, заметим, что при наложении фигуры Ф на равную ей фигуру Ф|, как мы представляем его наглядно, каждая точка фигуры Ф накладывается на некоторую точку фигуры Ф1. Иначе говоря, каждая точка фигуры Ф сопоставляется некоторой точке фигуры Ф1.

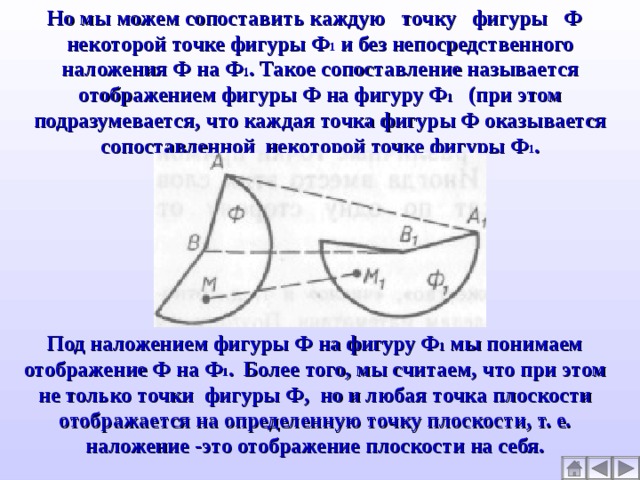
Но мы можем сопоставить каждую точку фигуры Ф некоторой точке фигуры Ф 1 и без непосредственного наложения Ф на Ф 1 . Такое сопоставление называется отображением фигуры Ф на фигуру Ф 1 (при этом подразумевается, что каждая точка фигуры Ф оказывается сопоставленной некоторой точке фигуры Ф 1 .

Под наложением фигуры Ф на фигуру Ф 1 мы понимаем отображение Ф на Ф 1 . Более того, мы считаем, что при этом не только точки фигуры Ф, но и любая точка плоскости отображается на определенную точку плоскости, т. е. наложение -это отображение плоскости на себя.

Однако не всякое отображение плоскости на себя мы называем наложением. Наложения — это такие отображения плоскости на себя, которые обладают свойствами, выраженными в аксиомах (см. ниже аксиомы 7—13). Чтобы сформулировать эти аксиомы, введем понятие равенства фигур. Пусть Ф и Ф 1 — две фигуры. Если существует наложение, при котором фигура Ф отображается на фигуру Ф 1 , то мы говорим, что фигуру Ф можно совместить наложением с фигурой Ф 1 , или что фигура Ф равна фигуре Ф 1 . Сформулируем теперь аксиомы о свойствах наложений.

7. Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.

8. На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.

Это означает, что если даны какой-то отрезок АВ и какой-то луч h с началом в точке О, то на луче h существует, и притом только одна, точка С, такая, что отрезок АВ равен отрезку ОС.

9. От любого луча в данную полуплоскость можно отложить угол, равный данному неразвернутому углу, и притом только один.

Это означает, что если даны какой-то луч ОА и какой-то неразвернутый угол СОЕ, то в каждой из двух полуплоскостей с границей ОА существует, и притом только один, луч ОВ, такой, что угол СОЕ равен углу АОВ.

10. Любой угол hk можно совместить наложением с равным ему углом h 1 k 1 двумя способами: 1) так, что луч h совместится с лучом h 1 , а луч k — с лучом k 1 ; 2) так, что луч h совместится с лучом k 1 , а луч k — с лучом h 1 .

11. Любая фигура равна самой себе.

12. Если фигура Ф равна фигуре Ф 1 , то фигура Ф 1 , равна фигуре Ф.

13. Если фигура Ф 1 равна фигуре Ф 2 , а фигура Ф 2 равна фигуре Фз, то фигура Ф 1 равна фигуре Фз.

Как видно, все приведенные аксиомы соответствуют нашим наглядным представлениям о наложении и равенстве фигур и поэтому не вызывают сомнений.

Следующие две аксиомы связаны с измерением отрезков. Прежде чем их сформулировать, напомним, как измеряются отрезки. Пусть АВ — измеряемый отрезок, PQ — выбранная единица измерения отрезков. На луче АВ отложим отрезок AA 1 = PQ , на луче А 1 В — отрезок A 1 A 2 = PQ и т. д. до тех пор, пока точка А n не совпадет с точкой В либо точка В не окажется лежащей между А n и А n +1 . В первом случае говорят, что длина отрезка АВ при единице измерения PQ выражается числом n (или что отрезок PQ укладывается в отрезке АВ n раз). Во втором случае можно сказать, что длина отрезка АВ при единице измерения PQ приближенно выражается числом n . Для более точного измерения отрезок PQ делят на равные части, обычно на 10 равных частей, и с помощью одной из этих частей измеряют описанным способом остаток А n В.

14. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.

Кроме того, мы принимаем аксиому существования отрезка данной длины.

15. При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом.

Систему аксиом планиметрии завершает аксиома параллельных прямых.

16. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Отметим, что для построения геометрии можно использовать различные системы аксиом. Например, вместо аксиомы параллельных прямых можно принять в качестве аксиомы утверждение о том, что сумма углов треугольника равна 180°. Тогда утверждение «Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной» можно доказать как теорему.

От различных систем аксиом требуется лишь, чтобы они были эквивалентны, т. е. приводили бы к одним и тем же выводам.

Иногда стремятся к тому, чтобы аксиомы были независимы, т. е. ни одну из них нельзя было вывести из остальных. Мы не ставили перед собой такой цели. Например, утверждение аксиомы 5 может быть доказано на основе остальных аксиом, т. е. фактически это утверждение является теоремой, а не аксиомой. Однако для упрощения изложения мы приняли его в качестве аксиомы.

В заключение рассмотрим одну из самых первых теорем нашего курса — теорему, выражающую первый признак равенства треугольников. Ее доказательство опиралось на наглядные представления о наложении и равенстве фигур, понятие аксиомы тогда еще не было введено. Напомним это доказательство и рассмотрим его с точки зрения принятых нами аксиом.

Нужно было доказать, что если АВ = А 1 В 1 , АС = А 1 С 1 и ∟ А= ∟ А 1 , то треугольники ABC и А 1 В 1 С 1 равны. С этой целью мы рассматривали такое наложение, при котором вершина А совмещается с вершиной А 1 , а стороны АВ и АС треугольника ABC накладываются соответственно на лучи А 1 С 1 и А 1 В 1 . При этом мы опирались на наглядно очевидный факт, что такое наложение существует, поскольку углы А и А 1 равны. Теперь можно сказать, что существование такого наложения следует из аксиомы 10. Далее мы рассуждали так: поскольку АВ = А 1 В 1 , АС = А 1 С 1 , то сторона АВ совместится со стороной А 1 В 1 , а сторона АС — со стороной А 1 С 1 , в частности совместятся точки В и В 1 , С и С 1 . Как обосновать этот факт, опираясь на аксиомы? Очень просто. По аксиоме 8 на луче A 1 B 1 от точки А 1 можно отложить только один отрезок, равный отрезку АВ. Но по условию теоремы АВ=А 1 В 1 , поэтому при нашем наложении точка В совместится с точкой В 1 . Аналогично точка С совместится с точкой С 1 .

Остается сослаться на аксиому 7, чтобы обосновать тот факт, что сторона ВС совместится со стороной В 1 С 1 . Теперь можно сделать вывод, что треугольники ABC и А 1 В 1 С 1 полностью совместились и, значит, они равны.

Как видим, само доказательство теоремы о первом признаке равенства треугольников, по существу, не изменилось, только теперь мы опирались уже не на наглядно очевидные факты, а на аксиомы, в которых эти факты выражены.

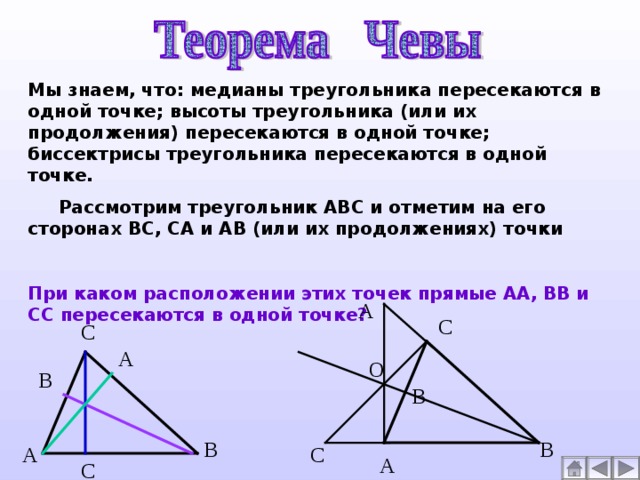
Мы знаем, что: медианы треугольника пересекаются в одной точке; высоты треугольника (или их продолжения) пересекаются в одной точке; биссектрисы треугольника пересекаются в одной точке.

Рассмотрим треугольник АВС и отметим на его сторонах ВС, СА и АВ (или их продолжениях) точки

При каком расположении этих точек прямые АА, ВВ и СС пересекаются в одной точке?

Обозначения:

пусть АВ и С - ненулевые коллинеарные векторы.

Обозначим через отношение длин этих векторов, взятое со знаком «+», если векторы сонаправлены, и со знаком «-», если они противоположно направлены. Сформулируем теперь теорему Чевы.

ТЕОРЕМА. Пусть в треугольнике АВС на сторонах ВС, СА и АВ или их продолжениях взяты соответственно точки А, В и С, не совпадающие с вершинами треугольника. Тогда если прямые АА, ВВ и СС пересекаются в одной точке или попарно параллельны, то

(1)

Обратно. Если выполнено равенство (1), то прямые АА 1 , ВВ 1 и СС 1 либо пересекаются в одной точке, либо попарно параллельны.

Доказательство:

Допустим сначала, что прямые АА1, ВВ1 и СС1 пересекаются в точке О. Для удобства условимся обозначать через площадь треугольника PQR , взятую со знаком «+», если обход вершин P, Q, R совершается против часовой стрелки, и со знаком «-», если по часовой стрелке.

Имеем , откуда

Аналогично

откуда

Следовательно

Итак,

Аналогично

Перемножая эти равенства и замечая, что

получаем

т.е. справедливо равенство (1).

Допустим, что теперь выполнено равенство (1)

Рассмотрим прямые АА 1 и ВВ 1 и предположим, что они пересекаются в некоторой точке О. Проведем прямую СО и обозначим через С 2 точку пересечения этой прямой с прямой АВ. Согласно

Из этого равенства и равенства (1) следует, что

Обозначив эти отношения λ , получаем

Вычтем одно равенство из другого:

Заметим теперь, что

(иначе получилось бы, что

Т.е.

А этого не может быть, т.к. точки А и В не совпадают)

Следовательно, т.е. точки С 1 и С 2 совпадают. Но это и означает, что прямые АА 1 , ВВ 1 и СС 1 пересекаются в одной точке

(в точке О).

Теорема доказана.

Для вывода вопроса выберите нужный сектор

Автор труда «Геометрия» (1637)?

Ответ

Р. Декарт

В начало

Кто из ученых доказал 5 постулат?

Ответ

Николай Иванович

Лобачевский

В начало

Из какой страны дошло до нас первое сочинение, содержащее простейшие геометрические сведения?

Ответ

Древний Египет

В начало

Сформулируйте теорему Чевы

Ответ

(1)

В начало

Перечислите три аксиомы, характеризующие взаимное расположение точек и прямых

Ответ

1. Каждой прямой принадлежат по крайней мере две точки.

2. Имеются по крайней мере три точки, не лежащие на одной прямой.

3. Через любые две точки проходит прямая, и притом только одна.

В начало

Какие аксиомы, связанные с понятиями наложения и равенства фигур вы запомнили?

Ответ

7. Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки.

8. На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.

10. Любой угол hk можно совместить наложением с равным ему углом h 1 k 1 двумя способами: 1) так, что луч h совместится с лучом h 1, а луч k — с лучом k 1; 2) так, что луч h совместится с лучом k 1, а луч k — с лучом h 1.