"Координатная плоскость"

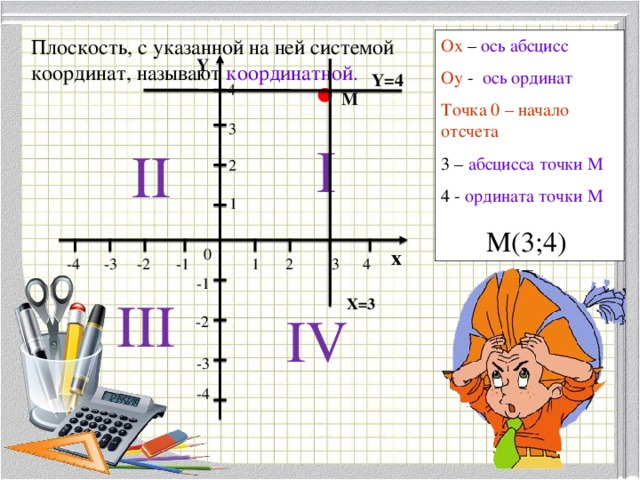
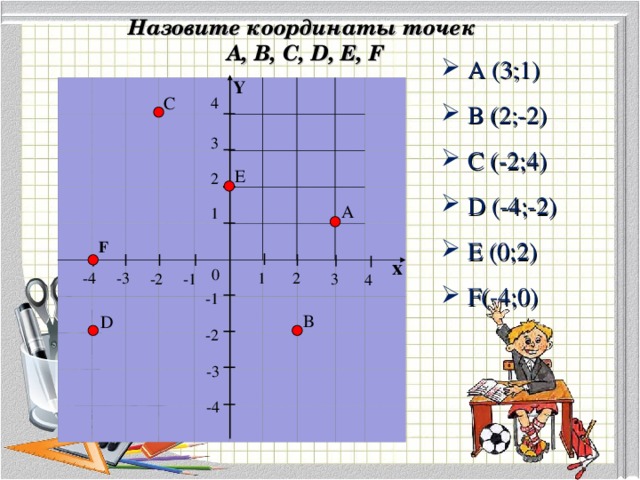
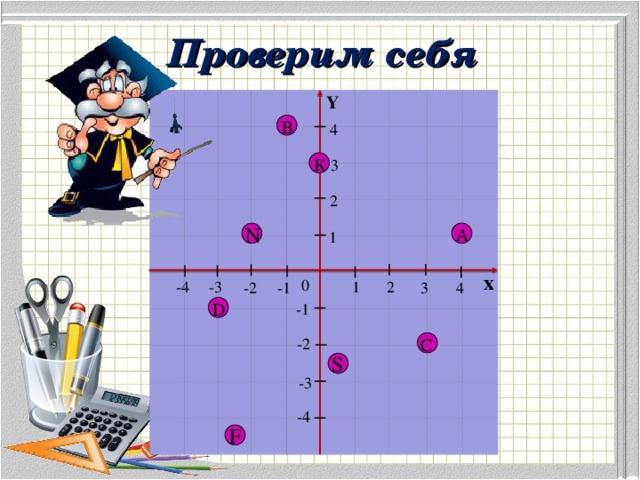
Тема "Координатная плоскость" у обучающихся вызывает заслуженный интерес. Можно дополнить задания учебника различными творческими задачами на построение фигур в прямоугольной системе координат. Предлагаю Вашему вниманию мини-презентацию, которую можно использовать на уроке для объяснения нового материала.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«"Координатная плоскость"»

Урок алгебры в 7 классе по теме «Координатная плоскость»

«Если действовать не будешь, ни к чему ума палата» Шота Руставели

Цель: формирование навыка отыскания координат точки и навыка построения точки по заданным координатам в прямоугольной системе координат

-5 -4 -3 -2 -1 0 1 2 3 4 5 6

Как называется прямая, изображенная на рисунке?

Назовите координаты точек

А, В , C, D, О .

А(4), В(-4), С(5,5), D (-1,5), О(0)

Числа, с помощью которых указывают, где находится некоторый объект, называют его координатами.

( от латинских слов ко – «совместно»

ординатус – «определенный»)

Плоскость, с указанной на ней системой координат, называют координатной .

О x – ось абсцисс

О y - ось ординат

Точка 0 – начало отсчета

3 – абсцисса точки М

4 - ордината точки М

М(3;4)

Y =4

-4

-1

-2

-3

-1

III

Х=3

-2

-3

-4

Прямоугольная система координат, состоящая из двух взаимно перпендикулярных осей с общим началом, изобретена в XVI в. Знаменитым французским математиком Рене Декартом.

Декартова система координат дала возможность объединить числовую и геометрическую линию математики.

Назовите координаты точек

А, В, С, D , Е, F

A (3;1)
B (2; - 2)
C (-2;4)
D (-4;-2)
E (0;2)
F(-4;0)

-3

-4

-2

-1

-2

-3

-4

Это нужно знать:

Если точка лежит на оси ординат, ее абсцисса равна нулю.

2. Если точка лежит на оси абсцисс, ее ордината равна нулю.

Начертите в тетради координатные оси, взяв единичный отрезок 1 см.

Постройте точки:

А (4;1), В (-1;4), С (3;-2),

D (-3;-1); К (0;3), N (-2; 1 )

F (-2,5;-4,5), S (0,5;-2,5)

Проверим себя

-3

-4

-2

-1

-2

-3

-4

Постройте фигуру, последовательно соединив отрезками точки с координатам и

(3; 7), (1; 5), (2; 4), (4; 3), (5; 2), (6; 2),

(8; 4), (8;-1), (6; 0), (0;-3), (2;-6), (-2;-3),

(-4;-2), (-5;-1), (-6; 1), (-6; 2), (-3; 5), (3; 7) Отдельно: (-3; 3) Отдельно: (-6; 1), (-4; 1) Отдельно: (-3; 5), (-2; 2), (-2; 0), (-4;-2) (за единичный отрезок примите 1 клетку тетради)

Всем спасибо

за работу!

Предмет: Математика

Категория: Презентации

Целевая аудитория: 7 класс

Скачать
"Координатная плоскость"

Автор: Вальковский Никита Михайлович

Дата: 25.01.2016

Номер свидетельства: 282478

Похожие файлы

Конспект урока по математике "Координатная плоскость" (6 класс)

object(ArrayObject)#855 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(115) "Конспект урока по математике "Координатная плоскость" (6 класс) "
    ["seo_title"] => string(62) "konspiekt-uroka-po-matiematikie-koordinatnaia-ploskost-6-klass"
    ["file_id"] => string(6) "119006"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1413305218"
  }
}

Конспект урока к уроку по математике по теме "Координатная плоскость"

object(ArrayObject)#877 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(129) "Конспект урока к уроку по математике  по теме "Координатная плоскость" "
    ["seo_title"] => string(72) "konspiekt-uroka-k-uroku-po-matiematikie-po-tiemie-koordinatnaia-ploskost"
    ["file_id"] => string(6) "109296"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1404312671"
  }
}

Координатная плоскость.

object(ArrayObject)#855 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(45) "Координатная плоскость. "
    ["seo_title"] => string(24) "koordinatnaia-ploskost-1"
    ["file_id"] => string(6) "104908"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1402769025"
  }
}

Учебный проект по математике "Координаты и координатная плоскость"

object(ArrayObject)#877 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(125) "Учебный проект по математике  "Координаты и координатная плоскость" "
    ["seo_title"] => string(69) "uchiebnyi-proiekt-po-matiematikie-koordinaty-i-koordinatnaia-ploskost"
    ["file_id"] => string(6) "124008"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1414609327"
  }
}

Открытый урок по теме: "Координатная плоскость"

object(ArrayObject)#855 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(88) "Открытый урок по  теме: "Координатная плоскость" "
    ["seo_title"] => string(46) "otkrytyi-urok-po-tiemie-koordinatnaia-ploskost"
    ["file_id"] => string(6) "195867"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1427974282"
  }
}

"Координатная плоскость"

Просмотр содержимого документа «"Координатная плоскость"»

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«"Координатная плоскость"»