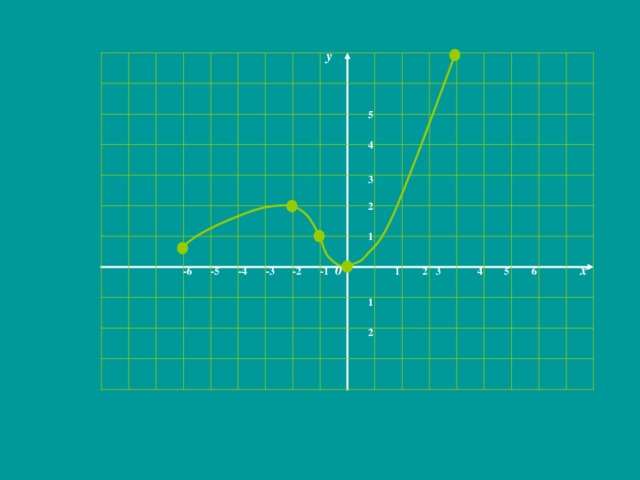Цель урока: способствовать развитию навыков чтения графиков и построения графиков функций, используя схему исследования функций.I.РАБОТА С УЧЕБНИКОМ
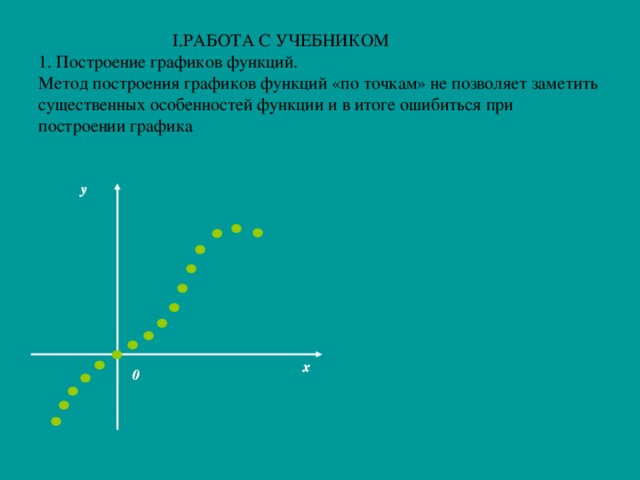
1. Построение графиков функций.
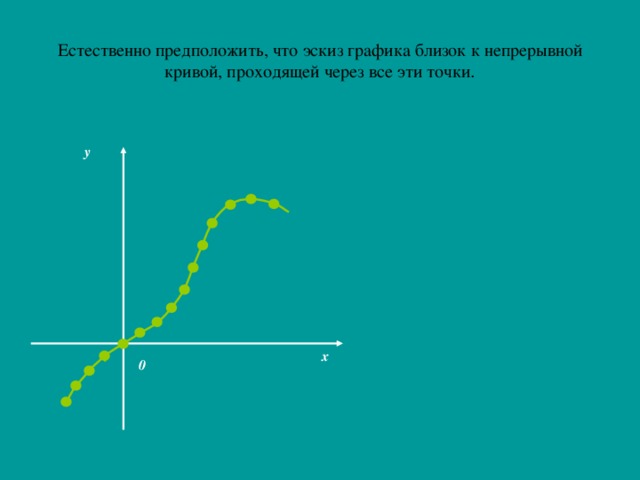
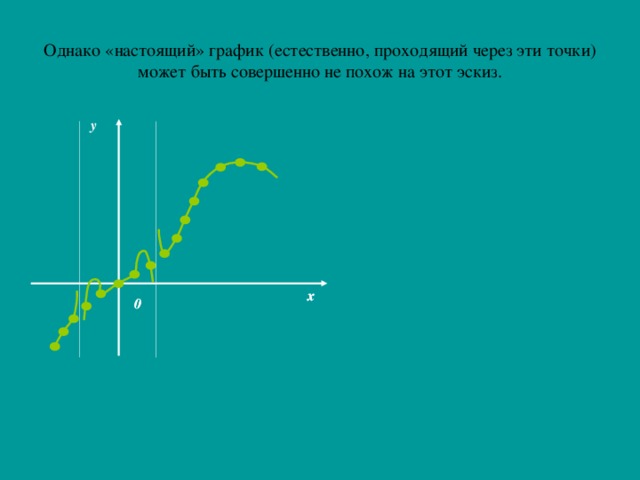
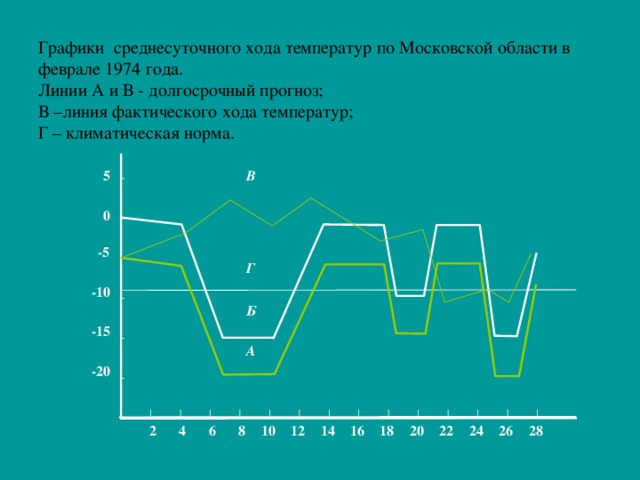
Метод построения графиков функций «по точкам» не позволяет заметить существенных особенностей функции и в итоге ошибиться при построении графика
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
"Исследование функций"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«"Исследование функций" »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1720 руб.
2860 руб.
1720 руб.
2860 руб.
1720 руб.
2860 руб.
1490 руб.
2480 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


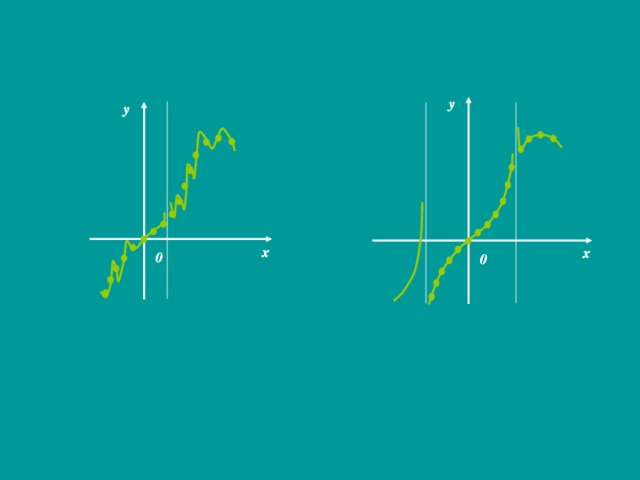

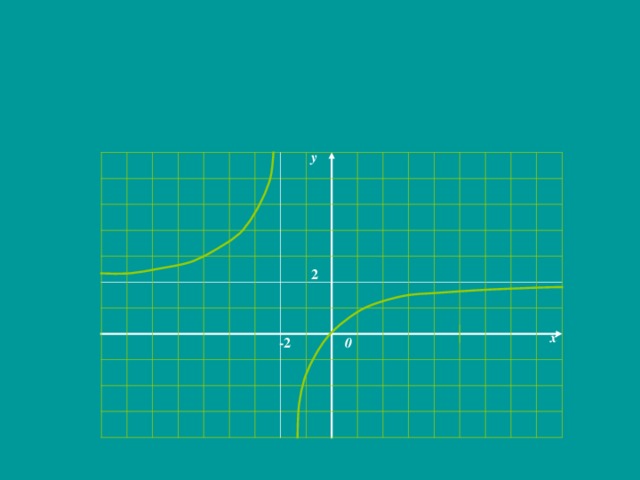
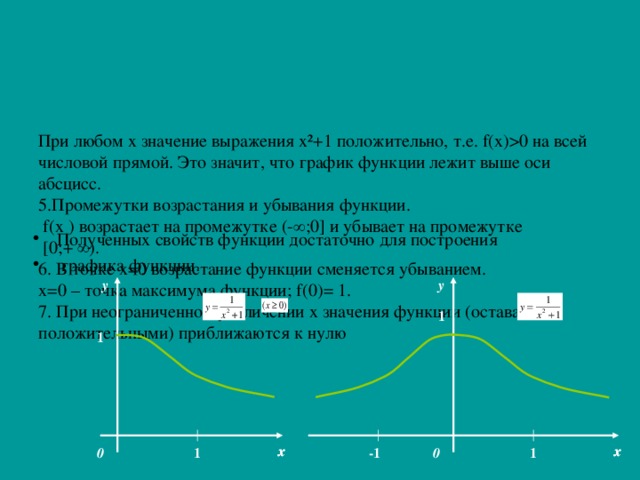 0 на всей числовой прямой. Это значит, что график функции лежит выше оси абсцисс. 5.Промежутки возрастания и убывания функции. f (х ) возрастает на промежутке (-∞;0] и убывает на промежутке [0;+ ∞). 6. В точке х=0 возрастание функции сменяется убыванием. х=0 – точка максимума функции; f (0)= 1. 7. При неограниченном увеличении х значения функции (оставаясь положительными) приближаются к нулю Полученных свойств функции достаточно для построения графика функции . y y 1 1 x x x x x x 1 0 1 0 -1" width="640"
0 на всей числовой прямой. Это значит, что график функции лежит выше оси абсцисс. 5.Промежутки возрастания и убывания функции. f (х ) возрастает на промежутке (-∞;0] и убывает на промежутке [0;+ ∞). 6. В точке х=0 возрастание функции сменяется убыванием. х=0 – точка максимума функции; f (0)= 1. 7. При неограниченном увеличении х значения функции (оставаясь положительными) приближаются к нулю Полученных свойств функции достаточно для построения графика функции . y y 1 1 x x x x x x 1 0 1 0 -1" width="640"

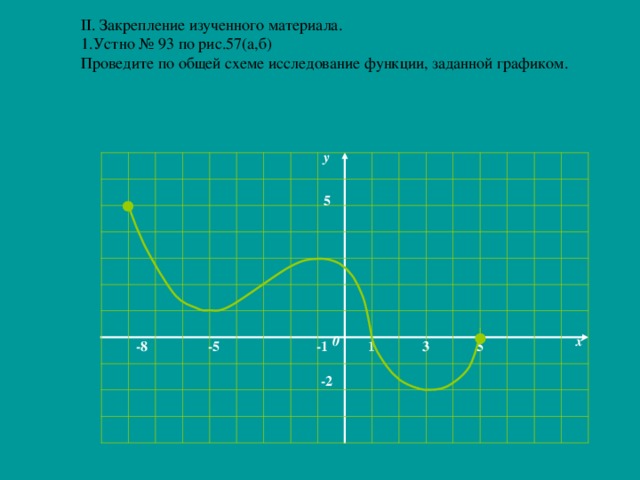
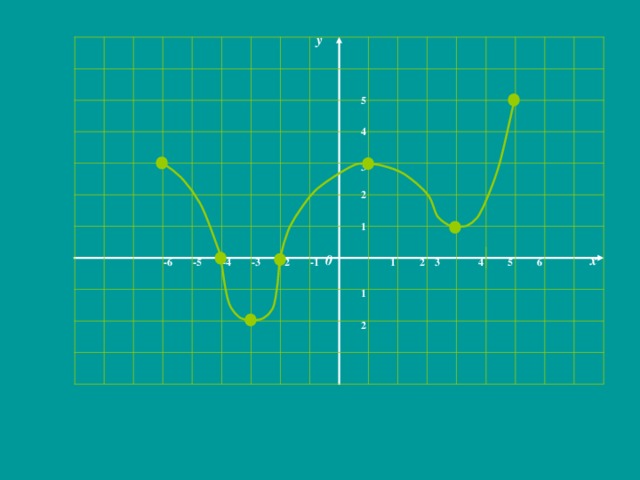
 0 б) f (х) 4. 5. О(0;0) [-6;-4); (-2;6] (-4;-2) Промежутки а) возрастания б) убывания Точки максимума, максимум функции. точки минимума, минимум функции [-5;0), (0;4] - [-3;1], [4;6] [-6;-3], [1;4] 6. [-5;-2] ;[0;4] [-2;0] 1, f (1) =3 -3, f (-3) = -2 4, f (4) =1 Дополнительные точки графика -2, f (-2) =2 0, f (0) =0 f (-6)=3 f (6) =5 f (-5) = 0,5 f (4) =6" width="640"
0 б) f (х) 4. 5. О(0;0) [-6;-4); (-2;6] (-4;-2) Промежутки а) возрастания б) убывания Точки максимума, максимум функции. точки минимума, минимум функции [-5;0), (0;4] - [-3;1], [4;6] [-6;-3], [1;4] 6. [-5;-2] ;[0;4] [-2;0] 1, f (1) =3 -3, f (-3) = -2 4, f (4) =1 Дополнительные точки графика -2, f (-2) =2 0, f (0) =0 f (-6)=3 f (6) =5 f (-5) = 0,5 f (4) =6" width="640"