Тема: «Умножение вектора на число».
Цель урока: совершенствовать навыки решения задач на применение свойств умножения вектора на число, развивать логическое мышление.
Ход урока
Презентация
I. Организационный момент
II. Актуализация знаний обучающихся
1. Фронтальный опрос:
а) дайте определение вектора;
б) какие векторы называются коллинеарными;
в) какой вектор называется произведением данного вектора на данное число;
Просмотр содержимого документа
«умножения вектора на число»
9 класс 20.09.2016
Тема: «Умножение вектора на число».
Цель урока: совершенствовать навыки решения задач на применение свойств умножения вектора на число, развивать логическое мышление.
Ход урока
Презентация
I. Организационный момент
II. Актуализация знаний обучающихся
1. Фронтальный опрос:
а) дайте определение вектора;
б) какие векторы называются коллинеарными;
в) какой вектор называется произведением данного вектора на данное число;
г) чему равно произведение 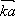 , если: а)
, если: а) 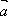 =
=  ; б) k=0?
; б) k=0?
д) могут ли векторы а и ka быть неколлинеарными?
е) сформулируйте основные свойства умножения вектора на число.
2. Устное решение задач на готовых чертежах.
Карточки для индивидуальной работы
I уровень (карточка № 1)
1. Даны два неколлинеарных вектора 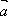 и
и 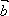 построить:
построить:
а) 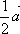 ; б) 2
; б) 2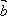 ; в)
; в) 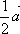 + 2
+ 2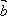 .
.
2. Дано: АВСD – параллелограмм, 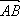 =
= 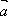 ,
, 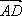 =
= 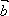 . Выразите
. Выразите 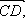
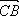 ,
, 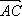 ,
, 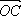 через
через 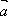 и
и 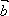
II уровень (карточка № 2)
1. Дан треугольник АВС. Построить векторы:
а) 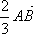 +
+ 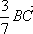 ; б) -
; б) -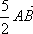 -
- 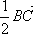 .
.
2 Дано: АВСD – параллелограмм, 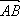 =
= 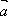 ,
, 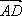 =
= 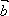 . Выразите
. Выразите 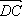 ,
, 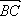 ,
,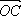 ,
, 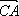 через
через 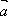 и
и 
III. Решение задач
1. Повторить свойства умножения вектора на число.

2. Решение задач:
а) № 781
б)
в)
IV.Самостоятельная работа
I уровень
Вариант 1
1. Начертит вектор  такой, что │
такой, что │ │= 2 см. Постройте векторы 3
│= 2 см. Постройте векторы 3 ; -2
; -2 ;
; 
 .
.
2. В параллелограмме АВСД на стороне АВ отмечена точка К так, что АК:КВ = 2:1 О – точка пересечения диагоналей. Выразите векторы  и
и 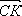 через векторы
через векторы 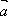 =
= 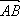 и
и  =
= 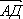 .
.
Вариант 2
1. Начертите вектор  , абсолютная величина которого равна 3 см. Постройте векторы 2
, абсолютная величина которого равна 3 см. Постройте векторы 2 ; -
; - ;
; 
 .
.
2. В параллелограмме АВСД на стороне ВС отмечена точка Р так, что ВР :РС = 3 :1 О – точка пересечения диагоналей. Выразите векторы  и
и  через векторы
через векторы 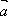 =
= 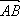 и
и  =
= 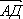 .
.
II уровень
1. Начертите два неколлинеарных вектора 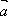 и
и  так, что │
так, что │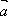 │= 2 см. и │
│= 2 см. и │ │= 3 см. Постройте вектор
│= 3 см. Постройте вектор 
 - 2
- 2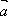 .
.
2. На сторонах ВС и СД параллелограмма АВСД взяты соответственно точки М и Е так, что М – середина ВС, СЕ : ЕД =1 :3. Выразите векторы  ,
,  ,
,  через векторы
через векторы  =
= 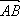 и
и  =
= 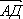 .
.
V. Подведение итогов урока
Оценить работу учащихся на уроке.
VI. Домашнее задание
П.86№775.776.778
Просмотр содержимого презентации
«умножения вектора на число»

Рисунки Савченко Е.М. Все рисунки в презентации выполнены с помощью инструментов панели рисования программы Microsoft PowerPoint .

Цель урока:
- Рассмотреть основные свойства умножения вектора на число
- Сформировать навыки решения задач на применение свойств умножения вектора на число
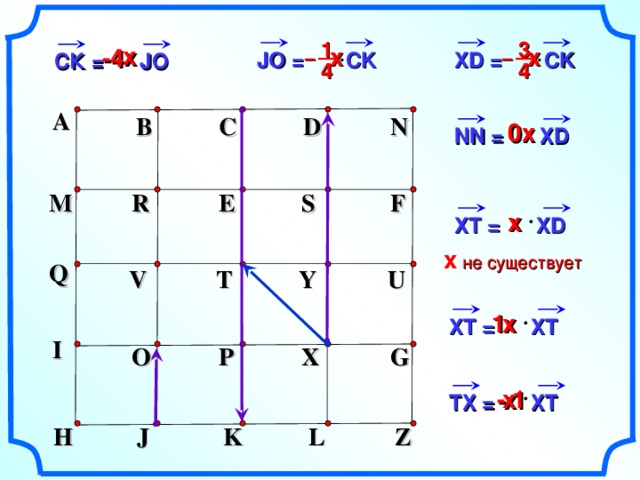
х
3
1
х
х
-4
JO = CK
XD = CK
–
–
СК = JO
4
4
A
B
N
D
C
х
0
NN = XD
M
R
E
S
F
х
ХТ = XD
х не существует
Q
V
U
Y
T
1
х
XT = XT
I
G
X
P
O
- 1
х
TX = XT
K
H
J
L
Z
3
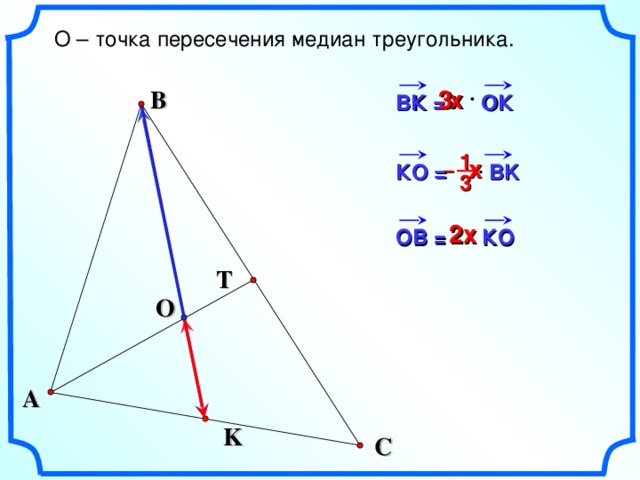
О – точка пересечения медиан треугольника.
3
B
х
ВК = ОК
1
х
–
К O = В K
3
х
2
ОВ = КО
T
O
A
K
C
4
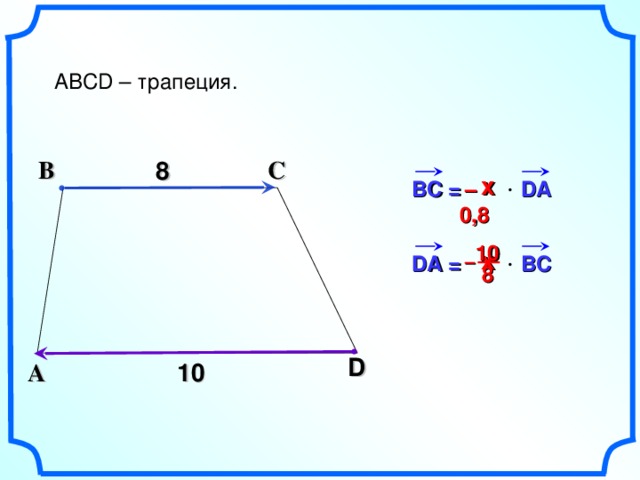
ABCD – трапеция.
С
В
8
х
– 0, 8
BC = DA
10
х
–
DA = BC
8
D
А
10
5

Умножение вектора на число обладает следующими основными свойствами.
a
b
b
l
k
Для любых , и любых чисел , справедливы равенства:
k (l a)
(kl)a =
1
Сочетательный закон
(k+l)a =
ka + la
2
«Геометрия 7-9» Л.С. Атанасян и др.
Первый распределительный закон
ka + kb
k (a + b) =
3
Второй распределительный закон
6
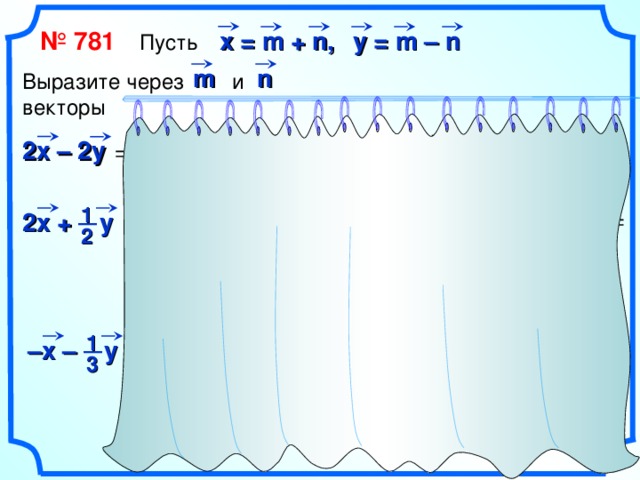
y = m – n
х = m + n,
№ 781 Пусть
n
m
Выразите через и
векторы
2х – 2у
1
2х + у
2
«Геометрия 7-9» Л.С. Атанасян и др.
1
– х – у
3
7
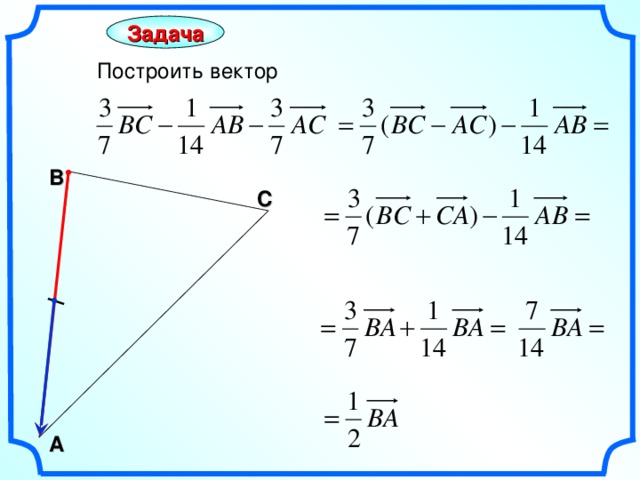
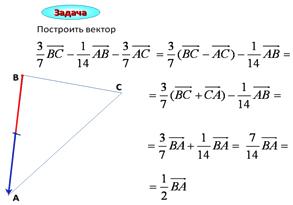
Задача
Построить вектор
В
С
Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)
А
7
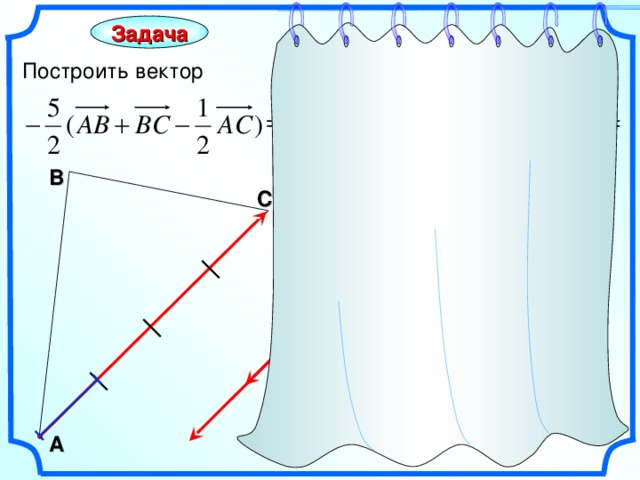
Задача
Построить вектор
В
С
Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)
А
9
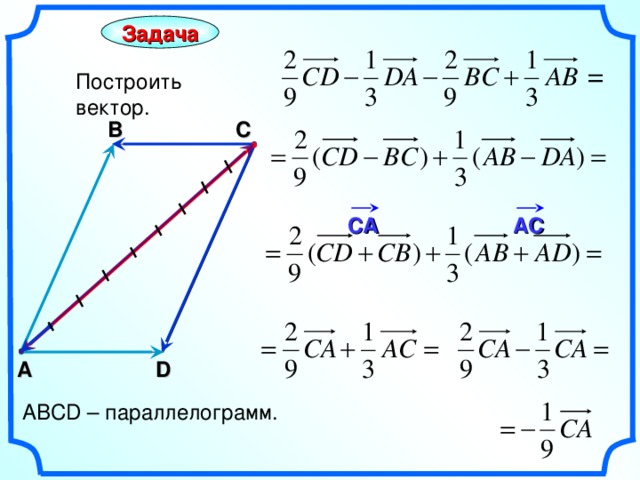
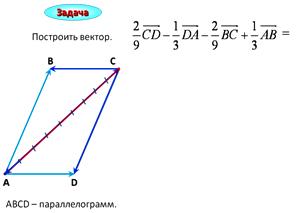
Задача
=
Построить вектор.
В
С
CA
AC
Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)
D
А
АВС D – параллелограмм.
10
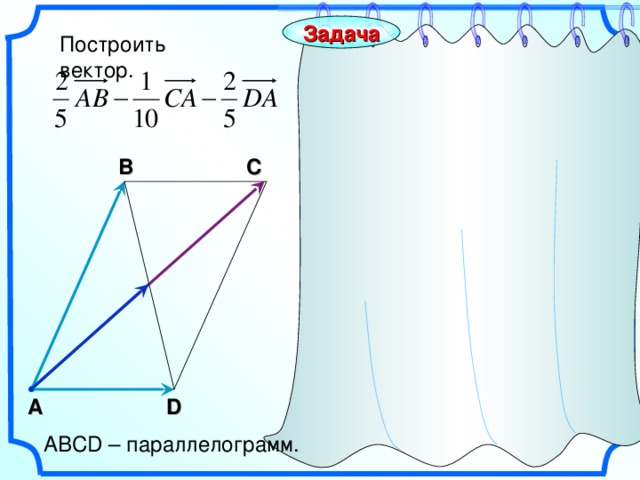
Задача
Построить вектор.
С
В
AC
Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)
D
А
АВС D – параллелограмм.
11
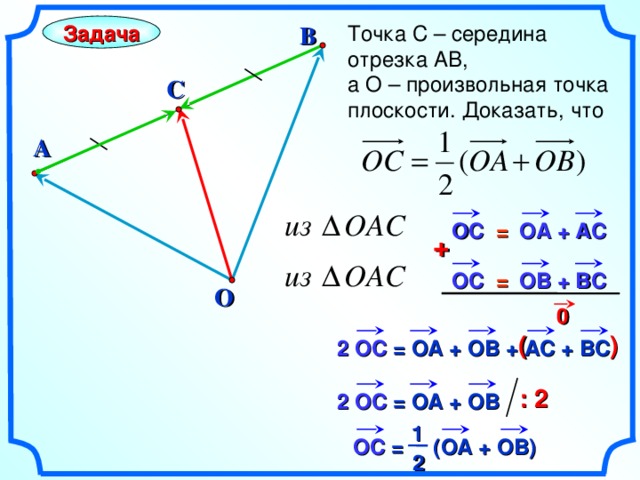
Точка С – середина отрезка АВ,
а О – произвольная точка плоскости. Доказать, что
B
Задача
C
A
O С =
O А + АС
+
O С =
O В + ВС
O
0
«Геометрия 7-9» Л.С. Атанасян и др.
( )
2 O С = ОА + ОВ + АС + ВС
: 2
2 O С = ОА + ОВ
1
O С = (ОА + ОВ)
2
12
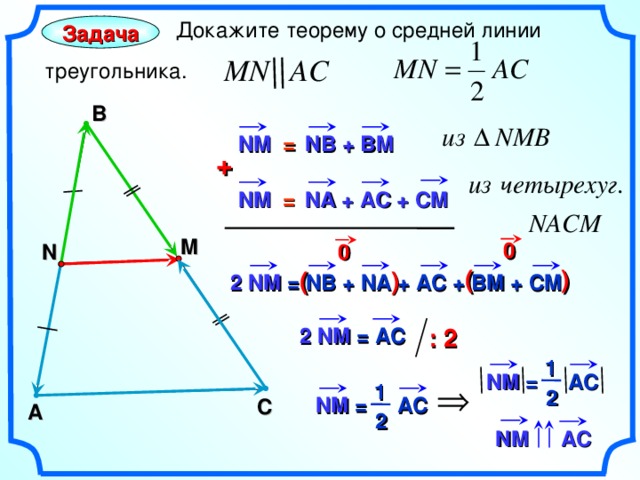
Докажите теорему о средней линии
треугольника.
Задача
В
NB + BM
NM =
+
NA + A С + CM
NM =
M
0
0
N
( )
( )
2 NM = NB + NA + АС + В M + CM
«Геометрия 7-9» Л.С. Атанасян и др.
2 NM = AC
: 2
1
NM = AC
1
2
NM = AC
С
A
2
NM
AC
13
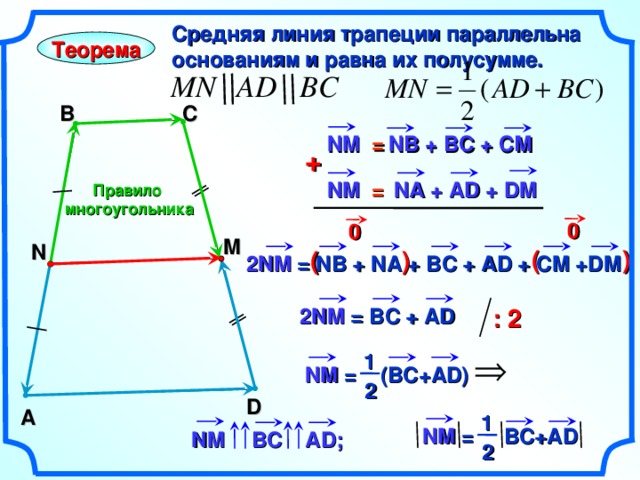
Средняя линия трапеции параллельна
основаниям и равна их полусумме.
Теорема
В
С
NB + B С + СМ
NM =
+
NA + AD + DM
NM =
Правило
многоугольника
0
0
M
N
( )
( )
2 NM = NB + NA + B С + AD + CM +DM
: 2
2 NM = В C + AD
«Геометрия 7-9» Л.С. Атанасян и др.
1
NM = (BC+AD)
2
D
A
1
NM = BC+AD
BC
AD;
NM
2
14
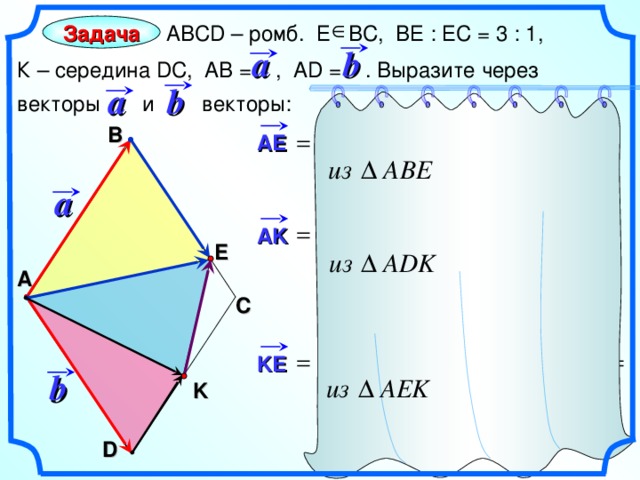
АВС D – ромб. Е ВС, ВЕ : ЕС = 3 : 1,
К – середина DC , АВ = , AD = . Выразите через
векторы и векторы:
Задача
b
a
a
b
В
AE
a
AK
E
А
С
Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)
KE
b
K
D
15



































