Рабочая программа по геометрии 8 класс (к учебнику Атанасяна Л.С.)

УТВЕРЖДАЮ ________________

Директор школы ФИО
«____» _____________ 2014 год

СОГЛАСОВАНО ________________

Зам. директора по УВР ФИО
«____» _____________ 2014 год

№ урока

Тема урока

Параграф учебника

Количество часов

Дидактические единицы

образовательного процесса

Контроль знаний учащихся

ЦОР и др. материалы

Дата

Глава 5. Четырёхугольники - 14 часов

1.

Многоугольники.

1

1

Знать какая фигура называется четырёхугольником, определение его составляющих;

Уметь изображать четырёхугольники, называть по рисунку его элементы;

Знать формулу суммы углов выпуклого многоугольника

2.

Многоугольники. Решение задач.

1

1

СР[2] с.26

3.

Параллелограмм.

2

1

Знать определение параллелограмма, свойства параллелограмма;

Уметь доказывать свойства параллелограмма и применять данные свойства при решении задач.

4.

Признаки параллелограмма.

2

1

Знать признаки параллелограмма;

Уметь доказывать признаки параллелограмма и применять их при решении несложных задач.

5.

Решение задач по теме «Параллелограмм»

2

1

Уметь применять полученные знания о параллелограмме при решении задач.

СР[2] с.44

6.

Трапеция.

2

1

Знать определение трапеции и её элементов;

Знать частные случаи трапеции (равнобедренная, прямоугольная).

7.

Теорема Фалеса.

2

1

Знать различные формулировки теоремы Фалеса;

СР[2] с.54

8.

Задачи на построение.

2

1

Уметь решать задания, используя теорему, делить отрезки и углы на равные части.

Уметь строить равнобедренную трапецию по трём заданным элементам.

9.

Прямоугольник.

3

1

Знать определение прямоугольника, свойство прямоугольника;

Уметь доказывать свойство прямоугольника, признак прямоугольника. Применять эти знания при решении задач.

10.

Ромб. Квадрат.

3

1

Знать определение ромба и его свойства;

Уметь доказывать свойство ромба , применять определение ромба, его свойства и признаки при решении задач.

Знать определение квадрата и его свойства;

Уметь решать задания, используя определение и свойства квадрата.

11.

Решение задач по теме «Прямоугольник. Ромб. Квадрат».

3

1

Знать все определения, свойства и признаки по изученной теме;

Уметь использовать знания при решении задач.

Тест[2] с.71

12.

Осевая и центральная симметрии.

3

1

Уметь строить симметричные точки;

Уметь распознавать фигуры, обладающие осевой и центральной симметрией

СР[2] с.77

13.

Решение задач по темам гл.5

1-3

1

Знать все определения, свойства и признаки по изученной теме;

Уметь использовать знания при решении задач.

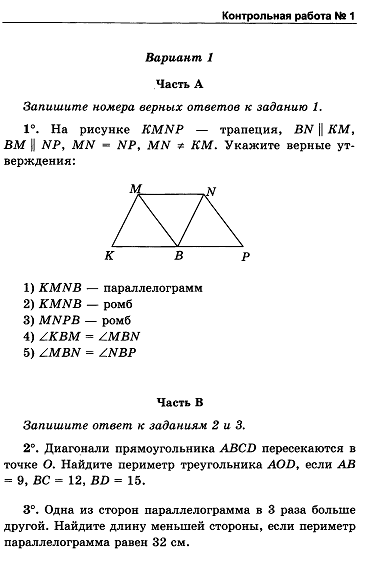
14.

Контрольная работа №1

по теме «Четырёхугольники»

1

Уметь применять изученную теорию к решению задач.

Глава 6. Площадь – 14 часов

15.

Площадь многоугольника.

1

1

Знать свойства площади;

Уметь находить площади фигур способом разбиения на квадраты.

16.

Площадь прямоугольника.

1

1

Знать формулу площади прямоугольника;

Уметь использовать при решении задач.

СР[2] с.102

17.

Площадь параллелограмма.

2

1

Знать формулу площади параллелограмма S = ah;

Уметь свободно применять её при решении задач.

18.

Площадь треугольника.

2

1

Знать формулу площади треугольника;

Уметь находить площадь прямоугольного треугольника;

Уметь находить площадь треугольника в случае, если равны их высоты или угол

19.

Площадь треугольника

2

1

20.

Площадь трапеции.

2

1

Знать формулу вычисления площади трапеции, которая равняется произведению полусуммы оснований на её высоту;

Уметь пользоваться этой формулой при решении задач.

21.

Решение задач на вычисление площадей фигур.

1-2

1

Уметь использовать изученные формулы при решении задач.

Тест[2] с.128

22.

Решение задач на нахождение площади.

1-2

1

СР[2] с.133

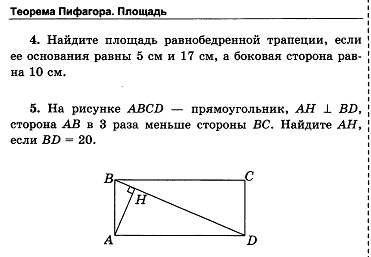
23.

Теорема Пифагора.

3

1

Знать теорему Пифагора;

Уметь доказывать теорему Пифагора и применять её при решении простейших задач.

24.

Теорема, обратная теореме Пифагора.

3

1

Знать теорему, обратную теореме Пифагора;

Уметь применять её при решении задач.

25.

Решение задач по теме «Теорема Пифагора».

3

1

Знать теорему Пифагора, теорему обратную теореме Пифагора;

Уметь определять египетский треугольник, использовать теоремы при решении задач.

СР[2] с.147

26.

Решение задач.

3

1

Уметь использовать изученные формулы при решении задач.

27.

Решение задач.

1-3

1

Знать формулы площади треугольника S = ah,
формулу Герона;

Уметь решать задачи на применение данных знаний.

28.

Контрольная работа №2

по теме «Теорема Пифагора. Площадь»

1-3

1

Уметь применять изученную теорию к решению задач.

Глава 7. Подобные треугольники – 19 часов

29.

Определение подобных треугольников.

1

1

Знать определение подобных треугольников;

Уметь указывать сходственные стороны и находить коэффициент подобия треугольников.

30.

Отношение площадей подобных треугольников.

1

1

Знать, что площади подобных треугольников относятся как квадраты их соответствующих линейных размеров, что с увеличением или уменьшением линейных размеров в k раз его площадь соответственно увеличивается или уменьшается в раз;

Уметь находить отношение площадей подобных треугольников по известным длинам пары соответствующих элементов этих фигур.

СР[2] с.175

31.

Первый признак подобия треугольников

2

1

Знать формулировку признака подобия по двум углам;

Уметь воспроизводить доказательство признака подобия и применять его для решения задач.

32.

Решение задач на применение первого признака подобия треугольников.

2

1

Уметь использовать знания при решении задач.

33.

Второй и третий признаки подобия треугольников.

2

1

Знать формулировку 2 и 3 признаков подобия;

Уметь применять признаки для решения задач.

34-35.

Решение задач на применение признаков подобия треугольников.

1-2

2

Уметь выбирать нужный признак подобия, анализируя условие задачи, и находить неизвестные элементы треугольников с его помощью.

СР[2] с.191

36.

Обобщающий урок по теме «Подобие треугольников»

1-2

1

Уметь применять изученную теорию к решению задач.

37-38.

Средняя линия треугольника. Свойство медиан треугольника.

3

2

Знать определение средней линии треугольника, её свойство, а также свойство медиан треугольника;

Уметь применять данные теоремы при решении задач.

СР[2] с.208

39-40.

Пропорциональные отрезки в прямоугольном треугольнике.

3

2

Уметь использовать утверждения о пропорциональных отрезках в прямоугольном треугольнике при решении задач.

СР[2] с.217

41.

Практические приложения подобия треугольников.

3

1

Уметь использовать свойства подобных треугольников при решении практических задач: определение высоты предмета и определение расстояния до недоступной точки.

42.

Задачи на построение методом подобия.

3

1

Уметь решать задачи на построение методом подобия.

43.

Синус, косинус и тангенс острого угла прямоугольного треугольника.

4

1

Уметь определять синус, косинус и тангенс острого угла прямоугольного треугольника;

Знать основное тригонометрическое тождество

44.

Значение синуса, косинуса и тангенса для углов 30⁰, 45⁰, 60⁰.

4

1

Знать числовые значения синуса, косинуса и тангенса углов 30, 45, 60;

Уметь применять данные числовые значения при решении задач.

45-46.

Соотношения между сторонами и углами прямоугольного треугольника. Решение задач.

3-4

2

Уметь решать прямоугольные треугольники.

Тест[2] с.239

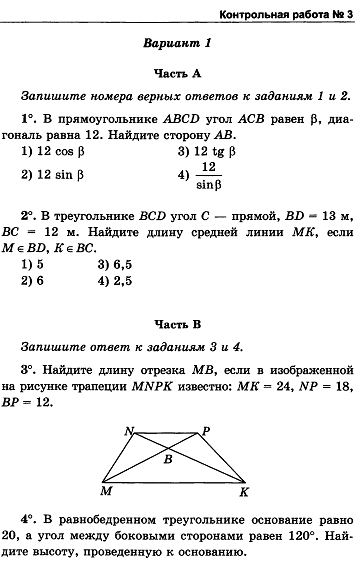
47.

Контрольная работа №3
по теме «Соотношения между сторонами и углами прямоугольного треугольника».

3-4

1

Уметь применять изученную теорию к решению задач.

Глава 8. Окружность – 17 часов

48.

Взаимное расположение прямой и окружности.

1

1

Знать все взаимные расположения прямой и окружности;

Уметь находить расстояние от точки до прямой.

49-50.

Касательная к окружности.

1

2

Знать определение, свойство и признак касательной; Уметь проводить через данную точку окружности касательную к этой окружности, решать задачи с применением данной теории.

СР[2] с.268

51.

Градусная мера дуги окружности.

2

1

Знать определение градусной меры дуги окружности и центрального угла;

Уметь решать простейшие задачи на вычисление градусной меры дуги окружности.

52.

Теорема о вписанном угле.

2

1

Знать определения центрального и вписанного углов, формулировку теоремы и следствий из этой теоремы;

Уметь при решении задач вычислять вписанные углы по соответствующим центральным углам и обратно, использовать в решении задач равенство вписанных углов, опирающихся на одну и ту же дугу окружности.

53.

Теорема об отрезках пересекающихся хорд.

2

1

Знать свойство отрезков пересекающихся хорд окружности;

Уметь применять свойство в решении несложных задач.

54.

Решение задач по теме «Центральные и вписанные углы»

1-2

1

Знать теоретический материал по изученной теме;

Уметь использовать знания при решении задач.

СР[2] с.283

55.

Свойство биссектрисы угла.

3

1

Знать прямую и обратную теоремы о биссектрисе угла;

Уметь использовать эти теоремы при решении задач.

56.

Серединный перпендикуляр.

3

1

Знать прямую и обратную теоремы о серединном перпендикуляре;

Уметь использовать эти теоремы при решении задач.

57.

Теорема о пересечении высот треугольника.

3

1

Знать теорему о пересечении высот треугольника;

Уметь строить 4 замечательные точки треугольника.

58.

Вписанная окружность.

4

1

Уметь вписывать окружность в многоугольник;

Уметь доказывать теорему о вписанной окружности и свойства

59.

Свойство описанного четырёхугольника.

4

1

Знать свойство сторон описанного четырёхугольника;

Уметь применять его при решении задач.

Тест[2] с.306

60.

Описанная окружность.

4

1

Уметь описывать окружность около многоугольника;

Уметь доказывать теорему об описанной окружности и замечания;

Знать, чему равна сумма противоположных углов вписанного многоугольника

61.

Свойство вписанного треугольника.

4

1

Знать свойство углов вписанного четырёхугольника;

Уметь применять его при решении задач.

63.

Решение задач по теме «Окружность».

1-4

2

Уметь определять градусную меру центрального и вписанного угла;

Уметь решать задачи с использованием замечательных точек треугольника;

Знать, чему равна сумма противоположных углов вписанного многоугольника

Тест[2] с.320

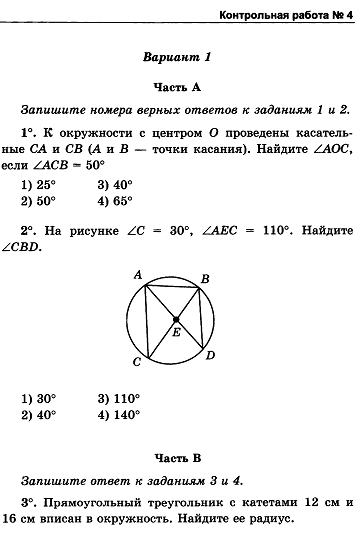
64.

Контрольная работа №4
по теме «Окружность».

1-4

1

Уметь применять изученную теорию к решению задач.

Итоговое повторение курса геометрии 8 класса – 4 часа

65.

Повторение темы «Четырёхугольники».

1

Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс геометрии 8 класса).

66.

Повторение темы «Площадь».

1

67.

Повторение темы «Подобие треугольников».

1

68.

Повторение темы «Окружность».

1